-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Giải bài 3.47 trang 44 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
Tính chiều cao của cây đó (làm tròn đến hàng đơn vị, theo đơn vị mét).
Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Trên sườn đồi, với độ dốc \(12\% \) (độ dốc của sườn đồi được tính bằng tang của một góc tạo bởi sườn đồi với phương nằm ngang) có một cây cao mọc thẳng đứng. Ở phía chân đồi, cách gốc cây 30m, người ta nhìn ngọn cây dưới một góc \({45^ \circ }\) so với phương nằm ngang. Tính chiều cao của cây đó (làm tròn đến hàng đơn vị, theo đơn vị mét).
Phương pháp giải - Xem chi tiết
- Tính góc BAH, góc CAB và góc BCA
- Áp dụng định lý sin để tính cạnh BC: \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\)
Lời giải chi tiết
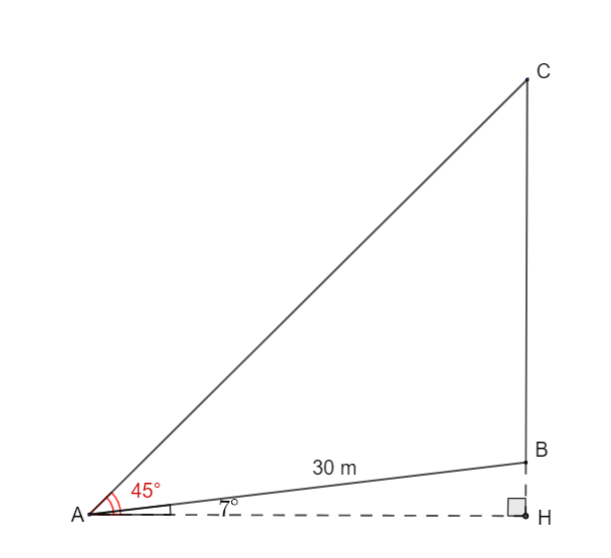
Do sườn đồi có độ dốc \(12\% \) nên sườn đồi tạo với phương nằm ngang một góc \(\tan HAB = 12\% \,\, \Rightarrow \,\,\widehat {HAB} = {\tan ^{ - 1}}\left( {12\% } \right) \approx {7^ \circ }\)
Ta có: \(\widehat {BAC} = \widehat {HAC} - \widehat {HAB} \approx {45^ \circ } - {7^ \circ } \approx {38^ \circ }\) và \(\widehat {BCA} = {45^ \circ }\)
Áp dụng định lý sin trong \(\Delta ABC,\) ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}}\\ \Rightarrow \,\,BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}}\\ \Rightarrow \,\,BC = \frac{{30.\sin {{38}^ \circ }}}{{\sin {{45}^ \circ }}} \approx 26\,\,\left( m \right)\end{array}\)
Bình luận
Chia sẻ- Giải bài 3.46 trang 44 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 3.45 trang 44 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 3.44 trang 44 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 3.43 trang 44 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 3.42 trang 44 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
