-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Giải bài 3.23 trang 40 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
Trên mặt phẳng tọa độ Oxy, lấy điểm M thuộc nửa đường tròn đơn vị,
Đề bài
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị, sao cho \(\cos \widehat {xOM} = \frac{{ - 3}}{5}.\) (H.3.4). Diện tích của tam giác \(AOM\) bằng:
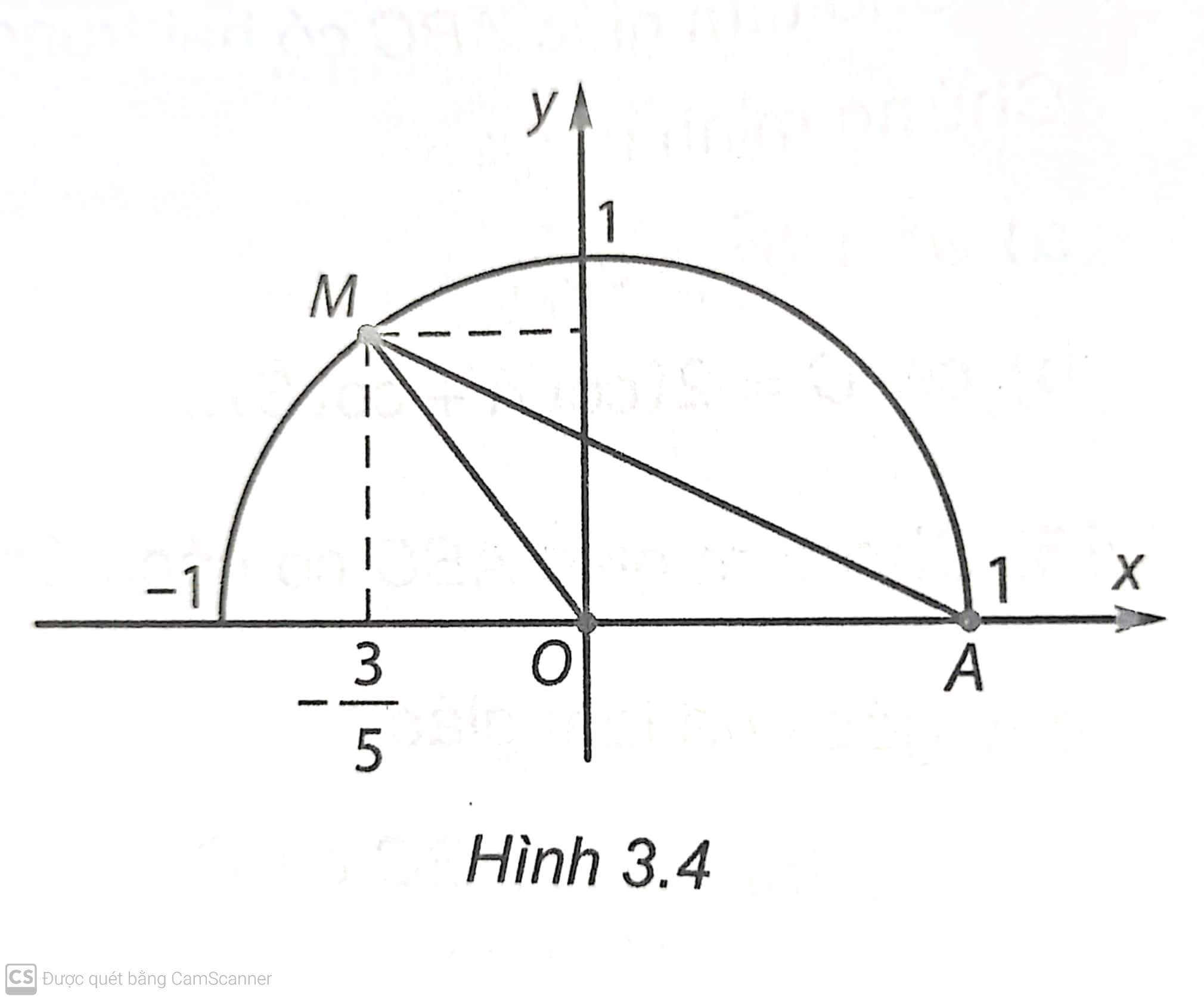
A. \(\frac{4}{5}.\)
B. \(\frac{2}{5}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{3}{{10}}.\)
Lời giải chi tiết
Ta có: \(\cos \widehat {xOM} = \frac{{ - 3}}{5} \Rightarrow \sin \widehat {xOM} = \sqrt {1 - {{\left( {\frac{{ - 3}}{5}} \right)}^2}} = \frac{4}{5}\)
Diện tích \(\Delta AOM\) là: \(S = \frac{1}{2}.OM.OA.sin AOM = \frac{1}{2}.1.1.\frac{4}{5} = \frac{2}{{5}}.\)
Chọn B.
Bình luận
Chia sẻ
- Giải bài 3.24 trang 41 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 3.25 trang 41 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 3.26 trang 41 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 3.27 trang 41 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 3.28 trang 41 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
Ph/hs Tham Gia Nhóm Để Cập Nhật Điểm Thi, Điểm Chuẩn Miễn Phí
