Bài 5. Vẽ góc cho biết số đo

Bài 23 trang 108 Vở bài tập toán 6 tập 2

Giải bài 23 trang 108 VBT toán 6 tập 2. Gọi Ot, Ot' là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O. Biết góc xOt bằng 30 độ, góc yOt' bằng 60 độ...

Đề bài

Gọi \(Ot, Ot'\) là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng \(xy\) đi qua \(O.\) Biết \(\widehat{xOt}=30^0,\) \(\widehat{yOt'}=60^0.\) Tính số đo các góc \(yOt, tOt'.\)

Phương pháp giải - Xem chi tiết

Hướng dẫn :

• Trước hết tính góc \(yOt\). Chú ý hai góc kề bù \(\widehat {xOt}\) và \(\widehat {yOt}\).

• So sánh hai góc \(\widehat {yOt'}\) và \(\widehat {yOt}\) để thấy tia nào nằm giữa trong ba tia \(Oy,\,Ot',\,Ot.\)

• Viết hệ thức giữa các góc \(\widehat {yOt'};\,\widehat {yOt}\) để tính \(\widehat {t'Ot}\).

Lời giải chi tiết

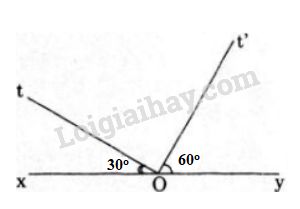
Ta có \(Ox,Oy\) là hai tia đối nhau nên \(\widehat {xOt}\) và \(\widehat {yOt}\) là hai góc kề bù.

Nên: \(\widehat{xOt}+\widehat{yOt}=180^0\)

\(\widehat{yOt}=180^\circ-\widehat{xOt}\) \(= 180^\circ-30^\circ=150^\circ \)

Hai tia \(Ot'\) và \(Ot\) cùng thuộc nửa mặt phẳng bờ \(Oy\) mà \(\widehat{yOt'}<\widehat{yOt}\) (vì \(60^0<150^0)\) nên tia \(Ot'\) nằm giữa hai tia \(Oy\) và \(Ot,\) suy ra

\(\widehat{yOt'}+\widehat{t'Ot}=\widehat{tOy}\)

Thay số ta được: \(60^\circ+\widehat{t'Ot}=150^\circ\)

Suy ra: \(\widehat{t'Ot}=150^\circ-60^\circ=90^\circ\)

Loigiaihay.com

Sub đăng ký kênh giúp Ad nhé !

Bình luận

Bình chọn:

4.4 trên 12 phiếu

Bài tiếp theo

Các bài liên quan: - Bài 5. Vẽ góc cho biết số đo

Luyện Bài tập trắc nghiệm môn Toán lớp 6 - Xem ngay

Báo lỗi - Góp ý Gửi góp ý ngay, nhận quà liền tay!

>> Học trực tuyến lớp 6 chương trình mới trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 6 học tốt, hoàn trả học phí nếu học không hiệu quả.