-
ĐẠI SỐ - SBT TOÁN 10 NÂNG CAO
-
Chương 1: Mệnh đề - Tập hợp
-
Chương 2: Hàm số
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT VÀ BẬC HAI
- Bài 1. Đại cương về phương trình
- Bài 2. Phương trình bậc nhất và bậc hai một ẩn
- Bài 3. Một số phương trình quy về phương trình bậc nhất hoặc bậc hai
- Bài 4. Phương trình và hệ phương trình bậc nhất nhiều ẩn
- Bài 5. Một số ví dụ về hệ phương trình bậc hai hai ẩn
- Bài tập Ôn tập chương III - Phương trình bậc nhất và bậc hai
-
CHƯƠNG IV. BẤT ĐẲNG THỨC VÀ BẤT PHƯƠNG TRÌNH
- Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
- Bài 2. Đại cương về bất phương trình
- Bài 3. Bất phương trình và hệ bất phương trình bậc nhất một ẩn
- Bài 4. Dấu của nhị thức bậc nhất
- Bài 5. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
- Bài 6. Dấu của tam thức bậc hai
- Bài 7. Bất phương trình bậc hai
- Bài 8. Một số phương trình và bất phương trình quy về bậc hai
- Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
-
CHƯƠNG V. THỐNG KÊ
-
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
-
BÀI TẬP ÔN TẬP CUỐI NĂM - ĐẠI SỐ 10 NÂNG CAO
-
-
HÌNH HỌC-SBT TOÁN 10 NÂNG CAO
Câu 4.64 trang 113 SBT Đại số 10 Nâng cao
Giải bài tập Câu 4.64 trang 113 SBT Đại số 10 Nâng cao
Giải các hệ bất phương trình và biểu hiện tập nghiệm của chúng trên trục số:
LG a
\(\left\{ \begin{array}{l}{x^2} - 4{ {x}} - 5 < 0\\{x^2} - 6{ {x}} + 8 > 0\\2{ {x}} - 3 \ge 0\end{array} \right.\)
Lời giải chi tiết:
Phương trình \({x^2} - 4{ {x}} - 5 = 0\) có hai nghiệm \({x_1} = - 1;{x_2} = 5,\) nên bất phương trình \({x^2} - 4{ {x}} - 5 < 0\) có tập nghiệm \({S_1} = \left( { - 1;5} \right).\)
Phương trình \({x^2} - 6{ {x}} + 8 = 0\) có hai nghiệm \({x_1} = 2;{x_2} = 4,\) nên bất phương trình \({x^2} - 6{ {x}} + 8 > 0\) có tập nghiệm \({S_2} = \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right).\)
Nghiệm của bất phương trình \(2{ {x}} - 3 \ge 0\) là \({S_3} = \left[ {\dfrac{3}{2}; + \infty } \right).\)
Suy ra nghiệm của hệ là giao của ba tập \({S_1},{S_2},{S_3},\) tức là
\(S = {S_1} \cap {S_2} \cap {S_3} = \left[ {\dfrac{3}{2};2} \right) \cup \left( {4;5} \right).\)
Biểu diễn trên trục số :
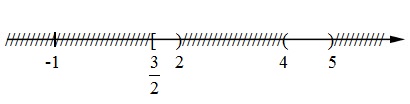
LG b
\(\left\{ \begin{array}{l}{x^2} - 12{ {x}} - 64 < 0\\{x^2} - 8{ {x + 15 > 0}}\\ - \dfrac{3}{4} \le x \le \dfrac{{13}}{2}.\end{array} \right.\)
Lời giải chi tiết:
\(S = \left[ { - \dfrac{3}{4};3} \right) \cup \left( {5;\dfrac{{13}}{2}} \right].\) Biểu diễn trên trục số :
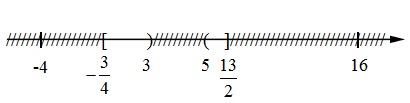
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 4.65 trang 113 SBT Đại số 10 Nâng cao
- Câu 4.66 trang 113 SBT Đại số 10 Nâng cao
- Câu 4.67 trang 113 SBT Đại số 10 Nâng cao
- Câu 4.68 trang 114 SBT Đại số 10 Nâng cao
- Câu 4.69 trang 114 SBT Đại số 10 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
