Câu 4.60 trang 112 SBT Đại số 10 Nâng cao

Giải bài tập Câu 4.60 trang 112 SBT Đại số 10 Nâng cao

Lựa chọn câu để xem lời giải nhanh hơn

Giải các bất phương trình :

LG a

\(\dfrac{{2{ {x}} - 5}}{{{x^2} - 6{ {x}} - 7}} < \dfrac{1}{{x - 3}}\)

Lời giải chi tiết:

Bất phương trình đã cho tương đương với bất phương trình :

\(\begin{array}{l}\dfrac{{2{ {x}} - 5}}{{{x^2} - 6{ {x}} - 7}} - \dfrac{1}{{x - 3}} < 0\\ \Leftrightarrow \dfrac{{\left( {2{ {x}} - 5} \right)\left( {{ {x}} - 3} \right) - \left( {{{ {x}}^2} - 6{ {x}} - 7} \right)}}{{\left( {{ {x}} - 3} \right)\left( {{ {x}} + 1} \right)\left( {{ {x}} - 7} \right)}} < 0\\ \Leftrightarrow \dfrac{{{{ {x}}^2} - 5{ {x}} + 22}}{{\left( {{ {x}} - 3} \right)\left( {{ {x}} + 1} \right)\left( {{ {x}} - 7} \right)}} < 0\,\,\,\,\,\,\,\,\,\,\left( * \right)\end{array}\)

Tam thức \({x^2} - 5{ {x}} + 22\) có \(a = 1 > 0,\) \(\Delta = - 63 < 0,\) nên \(\,{x^2} - 5{ {x}} + { {22 > 0}}\) với mọi \(x\). Suy ra (*) tương đương với \(\left( {{ {x}} - 3} \right)\left( {{ {x}} + 1} \right)\left( {{ {x}} - 7} \right) < 0.\)

Lập bảng xét dấu :

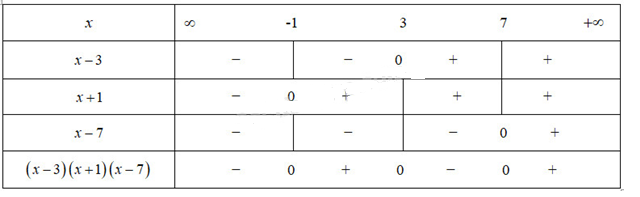
Từ bảng xét dấu suy ra tập nghiệm của bất phương trình đã cho là :

\(T = \left( { - \infty ; - 1} \right) \cup \left( {3;7} \right)\)

LG b

\(\dfrac{{{x^2} - 5{ {x + 6}}}}{{{x^2} + 5{ {x}} + 6}} \ge \dfrac{{x + 1}}{x}\)

Lời giải chi tiết:

Bất phương trình được biến đổi tương đương thành :

\(\dfrac{{11{{ {x}}^2} + 5{ {x}} + 6}}{{x\left( {{{ {x}}^2} + 5{ {x}} + 6} \right)}} \le 0.\)

Suy ra tập nghiệm là : \(S = \left( { - \infty ; - 3} \right) \cup \left( { - 2;0} \right).\)

LG c

\(\dfrac{2}{{{x^2} - x + 1}} - \dfrac{1}{{x + 1}} \ge \dfrac{{2{ {x}} - 1}}{{{x^3} + 1}}\)

Lời giải chi tiết:

Bất phương trình được biến đổi tương đương với :

\(\dfrac{{\left( {{ {x}} + 1} \right)\left( {2 - x} \right)}}{{\left( {{ {x}} + 1} \right)\left( {{{ {x}}^2} - x + 1} \right)}} \ge 0.\)

Suy ra tập nghiệm là : \(S = \left( { - \infty ; - 1} \right) \cup \left( { - 1;2} \right]\)

LG d

\(\dfrac{2}{x} + \dfrac{1}{{x - 1}} - \dfrac{1}{{x + 1}} \le 0.\)

Lời giải chi tiết:

Bất phương trình được biến đổi tương đương với :

\(\dfrac{{{x^2} + { {x}} - 1}}{{\left( {{ {x}} - 1} \right)\left( {{ {x}} + { {1}}} \right)x}} \le 0.\)

Suy ra tập nghiệm là : \(S = \left( { - \infty ;\dfrac{{ - 1 - \sqrt 5 }}{2}} \right] \cup \left( { - 1;0} \right) \cup \left[ {\dfrac{{ - 1 + \sqrt 5 }}{2};1} \right)\).

Loigiaihay.com