Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Bài 1. Tính đơn điệu của hàm số

Bài 4 trang 8 SGK Đại số và Giải tích 12 Nâng cao


Đề bài

Với các giá trị nào của a hàm số \(y = ax - {x^3}\) nghịch biến trên \(\mathbb R\)

Phương pháp giải - Xem chi tiết

- Tìm y'.

- Hàm số nghịch biến trên R khi và chỉ khi y'\(\le 0\) với mọi x.

Chú ý: Sử dụng định lý về dấu của tam thức bậc hai:

\(a{x^2} + bx + c \le 0\left( {a \ne 0} \right),\forall x \in R\) \(\Leftrightarrow \left\{ \begin{array}{l}
a < 0\\
\Delta \le 0
\end{array} \right.\)

Lời giải chi tiết

Cách 1:

Tập xác định \(D=\mathbb R\)

\(y' = a - 3{x^2}\)

Hàm số nghịch biến trên \(\mathbb{R}\) \( \Leftrightarrow y' \le 0,\forall x \in \mathbb{R}\)

\(\begin{array}{l} \Leftrightarrow  - 3{x^2} + a \le 0,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l} - 3 < 0\\\Delta  = {0^2} - 4.\left( { - 3} \right).a \le 0\end{array} \right.\\ \Leftrightarrow 12a \le 0\\ \Leftrightarrow a \le 0\end{array}\)

Cách 2. Hàm số nghịch biến trên R, điều kiện y'≤0,∀x ∈R,y'=0 chỉ tại một số hữu hạn điểm.

Ta có: y'≤0 ⇔ a-3x2≤0, ∀x

⇔ 3x2 ≥ a, ∀x ∈R

⇔ a≤min(3x2 ), mà 3x2≥0 ∀x ∈R

Nên \(\mathop {\min }\limits_\mathbb{R} \left( {3{x^2}} \right) = 0\). Vậy \(a \le 0\).

Kết luận: với a≤0 thì y=ax-3x3 nghịch biến trên R.

Cách 3:

Tập xác định \(D=\mathbb R\)

\(y' = a - 3{x^2}\)

• Nếu \(a < 0\) thì \(y' < 0\) với mọi \(x \in {\mathbb R}\), khi đó hàm số nghịch biến trên \(\mathbb R\).

• Nếu \(a = 0\) thì \(y' =  - 3{x^2} \le 0\) với mọi \(x \in {\mathbb R}\), \(y'=0\Leftrightarrow x=0\).

Vậy hàm số nghịch biến trên \(\mathbb R\).

• Nếu \(a > 0\) thì \(y' = 0\) \( \Leftrightarrow x =  \pm {\sqrt {a  \over 3}}\)

Ta có bảng biến thiên

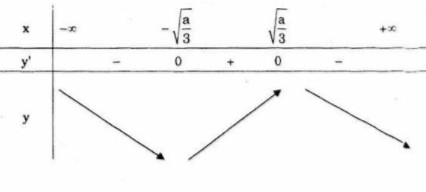
Trong trường hợp này, hàm số không đồng biến trên  \({\mathbb R}\)

Vậy hàm số nghịch biến trên \({\mathbb R}\) khi và chỉ khi \(a \le 0\).

Loigiaihay.com


Bình chọn:
3.6 trên 12 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2022 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua