 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Bài 3. Dạng lượng giác của số phức và ứng dụng
Bài 3. Dạng lượng giác của số phức và ứng dụng
Bài 31 trang 206 SGK giải tích 12 nâng cao
Chứng minh rằng
Cho các số phức \({\rm{w}}= {{\sqrt 2 } \over 2}\left( {1 + i} \right)\) và \(\varepsilon = {1 \over 2}\left( { - 1 + i\sqrt 3 } \right)\)
LG a
Chứng minh rằng \({z_o} = \cos {\pi \over {12}} + i\sin {\pi \over {12}},\,{z_1} = {z_o}\varepsilon ,\) \({z_2} = {z_o}{\varepsilon ^2}\) là các nghiệm của phương trình \({z^3} - {\rm{w}} = 0;\)
Lời giải chi tiết:
Ta có: \(w = \cos {\pi \over 4} + i\sin {\pi \over 4}\)
\(\eqalign{ & \varepsilon = \cos {{2\pi } \over 3} + i\sin {{2\pi } \over 3}\cr & \Rightarrow {\varepsilon ^3} = \cos 2\pi + i\sin 2\pi = 1 \cr & z_o^3 = {\left( {\cos {\pi \over {12}} + i\sin {\pi \over {12}}} \right)^3} \cr &= \cos {\pi \over 4} + i\sin {\pi \over 4} ={\rm{w}} \cr & z_1^3 = {\left( {{z_o}\varepsilon } \right)^3} = z_o^3.{\varepsilon ^3} = {\rm{w}} \,\,\left( {\text{vì}\,\,\,{\varepsilon ^3} = 1} \right), \cr & z_2^3 = {\left( {z_o{\varepsilon ^2}} \right)^3} = z_o^3{\varepsilon ^6} = z_o^3 ={\rm{w}}\cr} \)
Do đó các số phức \({z_0},{z_0}\varepsilon ,{z_0}{\varepsilon ^2}\) đều là nghiệm của phương trình \(z^3-w=0\).
Cách khác:
\(\begin{array}{l}{z_0} = \cos \dfrac{\pi }{{12}} + i\sin \dfrac{\pi }{{12}}\\ \Rightarrow z_0^3 = \cos \dfrac{{3\pi }}{{12}} + i\sin \dfrac{{3\pi }}{{12}}\\ = \cos \dfrac{\pi }{4} + i\sin \dfrac{\pi }{4}\\ = \dfrac{{\sqrt 2 }}{2} + i.\dfrac{{\sqrt 2 }}{2}\\ = \dfrac{{\sqrt 2 }}{2}\left( {1 + i} \right) = w\\ \Rightarrow z_0^3 = w \Rightarrow z_0^3 - w = 0\end{array}\)
\( \Rightarrow {z_0} = \cos \dfrac{\pi }{{12}} + i\sin \dfrac{\pi }{{12}}\) là nghiệm của phương trình \({z^3} - w = 0\).
\(\begin{array}{l}\varepsilon = \dfrac{1}{2}\left( { - 1 + i\sqrt 3 } \right) = - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\\ = \cos \dfrac{{2\pi }}{3} + i\sin \dfrac{{2\pi }}{3}\\{z_0} = \cos \dfrac{\pi }{{12}} + i\sin \dfrac{\pi }{{12}}\\ \Rightarrow {z_1} = {z_0}\varepsilon \\ = \cos \left( {\dfrac{{2\pi }}{3} + \dfrac{\pi }{{12}}} \right) + i\sin \left( {\dfrac{{2\pi }}{3} + \dfrac{\pi }{{12}}} \right)\\ = \cos \dfrac{{3\pi }}{4} + i\sin \dfrac{{3\pi }}{4}\\ \Rightarrow z_1^3 = \cos \dfrac{{9\pi }}{4} + i\sin \dfrac{{9\pi }}{4}\\ = \cos \dfrac{\pi }{4} + i\sin \dfrac{\pi }{4}\\ = \dfrac{{\sqrt 2 }}{2} + i.\dfrac{{\sqrt 2 }}{2} = w\\ \Rightarrow z_1^3 - w = 0\end{array}\)
\( \Rightarrow {z_1} = {z_0}\varepsilon \) là một nghiệm của phương trình \({z^3} - w = 0\).
\(\begin{array}{l}\varepsilon = \cos \dfrac{{2\pi }}{3} + i\sin \dfrac{{2\pi }}{3}\\ \Rightarrow {\varepsilon ^2} = \cos \dfrac{{4\pi }}{3} + i\sin \dfrac{{4\pi }}{3}\\ \Rightarrow {z_2} = {z_0}{\varepsilon ^2}\\ = \cos \left( {\dfrac{\pi }{{12}} + \dfrac{{4\pi }}{3}} \right) + i\sin \left( {\dfrac{\pi }{{12}} + \dfrac{{4\pi }}{3}} \right)\\ = \cos \dfrac{{17\pi }}{{12}} + i\sin \dfrac{{17\pi }}{{12}}\\ \Rightarrow z_2^3 = \cos \dfrac{{17\pi }}{4} + i\sin \dfrac{{17\pi }}{4}\\ = \cos \dfrac{\pi }{4} + i\sin \dfrac{\pi }{4}\\ = \dfrac{{\sqrt 2 }}{2} + i.\dfrac{{\sqrt 2 }}{2} = w\\ \Rightarrow z_2^3 - w = 0\end{array}\)
\( \Rightarrow {z_2} = {z_0}{\varepsilon ^2}\) là một nghiệm của phương trình \({z^3} - w = 0\).
LG b
Biểu diễn hình học các số phức \({z_o},\,{z_1},\,{z_2}\)
Lời giải chi tiết:
Biểu diễn: Các điểm A, B, C lần lượt biểu diễn \({z_0},\,\,{z_1},\,\,{z_2}\)
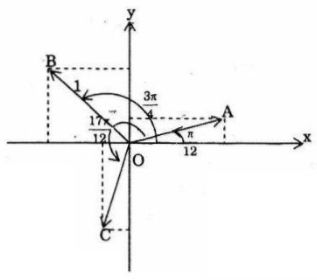
\(\begin{array}{l}
{z_0} = \cos \frac{\pi }{{12}} + i\sin \frac{\pi }{{12}}\\
{z_1} = \cos \frac{{3\pi }}{4} + i\sin \frac{{3\pi }}{4}\\
{z_2} = \cos \frac{{17\pi }}{{12}} + i\sin \frac{{17\pi }}{{12}}
\end{array}\)
Nhận xét: A,B,C tạo thành một tam giác đều.
Loigiaihay.com












Danh sách bình luận