Trắc nghiệm Bài 29. Các dạng bài tập thấu kính - Vật Lí 11
Đề bài
Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có độ tụ 2dp và cách thấu kính một khoảng 25cm. Khoảng cách từ ảnh A’B’ đến AB là:
-
A.
25cm
-
B.
35cm
-
C.
60cm
-
D.
50cm
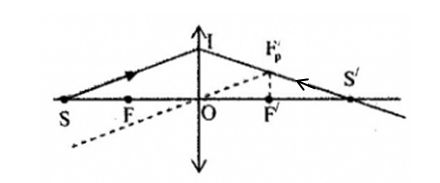
Ảnh S’ của điểm sáng S được đặt như hình là:
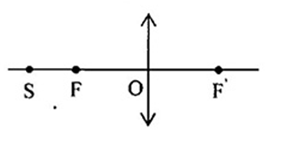
-
A.
-
B.
-
C.
-
D.
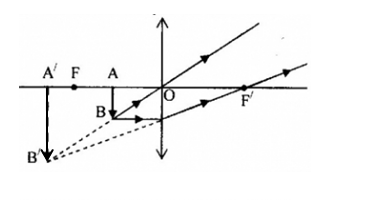
Chọn phương án đúng về cách vẽ ảnh A’B’ của vật sáng AB trong các trường hợp sau:
-
A.
-
B.
-
C.
-
D.
xy là trục chính của thấu kính, AB là vật thật, A’B’ là ảnh
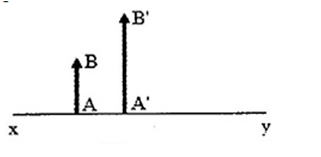
Hãy cho biết A’B’ là ảnh gì?
-
A.
ảnh ảo
-
B.
ảnh thật
-
C.
ảnh đối xứng
-
D.
không xác định được
thấu kính thuộc loại nào và vật được đặt trước hay sau thấu kính?
-
A.
Thấu kính hội tụ và vật đặt trước thấu kính
-
B.
Thấu kính hội tụ và vật đặt sau thấu kính
-
C.
Thấu kính phân kì và vật đặt trước thấu kính
-
D.
Thấu kính phân kì và vật đặt sau thấu kính
Trong hình sau, S- là điểm vật thật, S’- là điểm ảnh, xy - là trục chính thấu kính.
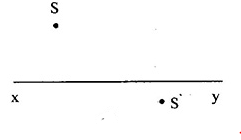
Hãy cho biết S’ là ảnh gì và thấu kính thuộc loại nào?
-
A.
ảnh ảo và thấu kính phân kỳ
-
B.
ảnh thật và thấu kính hội tụ
-
C.
ảnh ảo và thấu kính hội tụ
-
D.
ảnh thật và thấu kính phân kỳ
Gọi d là khoảng cách từ S đến thấu kính, d nằm trong khoảng nào?
-
A.
$d < {\text{OF}}$
-
B.
$d > {\text{OF}}$
-
C.
$d = {\text{OF}}$
-
D.
\({\text{0 < d < OF}}\)
Cho thấu kính hội tụ có tiêu cự f = 10cm. Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính, cách thấu kính 30cm. Tính chất của ảnh và số phóng đại ảnh là:
-
A.
ảnh ảo cùng chiều với vật, k = 0,5
-
B.
ảnh thật cùng chiều với vật, k = -0,5
-
C.
ảnh ảo ngược chiều với vật, k = 0,5
-
D.
ảnh thật ngược chiều với vật, k = -0,5
Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ và cách thấu kính 10cm. Nhìn qua thấu kính thấy một ảnh cùng chiều và cao gấp 3 lần vật. Tiêu cự của thấu kính có giá trị là:
-
A.
10cm
-
B.
25cm
-
C.
15cm
-
D.
5cm
Đặt một thấu kính cách một trang sách 20cm, nhìn qua thấu kính thấy ảnh của dòng chữ cùng chiều với dòng chữ nhưng cao bằng nửa dòng chữ thật. Thấu kính thuộc loại gì và tiêu cự có giá trị là bao nhiêu?
-
A.
Thấu kính hội tụ, f = 20cm
-
B.
Thấu kính phân kì, f = -20cm
-
C.
Thấu kính hội tụ, f =10cm
-
D.
Thấu kính phân kì, f = -10cm
Vật \(AB = 10cm\) là một đoạn thẳng song song với trục chính của một thấu kính hội tụ mỏng tiêu cự \(f = 20cm\). B gần thấu kính và cách thấu kính \(30cm\). Khoảng cách \(AB\) tới trục chính của thấu kính là \(h = 3cm\). Độ lớn của ảnh là:
-
A.
12cm
-
B.
40cm
-
C.
20,2cm
-
D.
24,6cm
Một thấu kính phân kì có tiêu cự f = -30cm. Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính cho ảnh cách vật 15cm. Vị trí của vật là:
-
A.
30cm
-
B.
-15cm
-
C.
15cm
-
D.
-30cm
Vật sáng AB đặt vuông góc với trục chính của một thấu kính phẳng lồi bằng thủy tinh chiết suất n =1,5 bán kính mặt lồi bằng 10cm , cho ảnh rõ nét trên màn đặt cách vật một khoảng L. Khoảng cách ngắn nhất của L là:
-
A.
40cm
-
B.
20cm
-
C.
80cm
-
D.
60cm
Đặt một vật sáng AB trước một thấu kính hội tụ có tiêu cự f =20cm. Cách vật AB một đoạn 90cm, người ta đặt một màn hứng. Ta phải đặt thấu kính ở vị trí cách vật bao nhiêu thì thu được ảnh rõ nét trên màn?
-
A.
30cm hoặc 60cm
-
B.
20cm hoặc 50cm
-
C.
25cm hoặc 75cm
-
D.
10cm hoặc 40cm
Một vật sáng AB cho ảnh thật qua một thấu kính hội tụ, ảnh này hứng trên một màn E đặt cách vật một khoảng 180cm, ảnh thu được cao bằng 1/5 vật. Tiêu cự của thấu kính có giá trị:
-
A.
15cm
-
B.
10cm
-
C.
5cm
-
D.
25cm
Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L = 72cm. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính, người ta tìm được vị trí của thấu kính cho ảnh rõ nét trên màn. Hai vị trí này cách nhau 48cm, tính tiêu cự của thấu kính?
-
A.
5cm
-
B.
10cm
-
C.
15cm
-
D.
20cm
Một thấu kính có dạng một mặt phẳng và một mặt cầu làm bằng thủy tinh có chiết suất n =1,5. Đặt trong không khí, một chùm sáng tới song song với trục chính cho chùm tia ló hội tụ tại điểm phía sau thấu kính, cách thấu kính 12cm. Bán kính của mặt cầu có giá trị là:
-
A.
2,5cm
-
B.
5cm
-
C.
3cm
-
D.
6cm
Một thấu kính thủy tinh có chiết suất n =1,5 đặt trong không khí có độ tụ 8dp. Khi nhúng thấu kính vào một chất lỏng nó trở thành một thấu kính phân kì có tiêu cự 1m. Chiết suất của chất lỏng là:
-
A.
1,2
-
B.
1
-
C.
1,6
-
D.
1,7
Một thấu kính hai mặt lồi cùng bán kính R, khi đặt trong không khí nó có tiêu cự f = 30cm. Nhúng chìm thấu kính vào một bể nước, cho trục chính của nó thẳng đứng rồi cho một chùm sáng song song rọi thẳng đứng từ trên xuống thì thấy điểm hội tụ cách thấu kính 80cm. R = ? Biết chiết suất của nước là 4/3.
-
A.
20cm
-
B.
40cm
-
C.
25cm
-
D.
35cm
Vật sáng AB đặt song song với một màn M, cách màn một đoạn L = 45 cm. Giữa vật và màn có một thấu kính hội tụ song song với vật và màn, trục chính của thấu kính đi qua A. Giữ cố định vật và màn, di chuyển thấu kính giữa vật và màn thì thấy có hai vị trí thấu kính cho hai ảnh trên màn, ảnh này gấp k = 4 lần ảnh kia. Tiêu cự thấu kính là
-
A.
15cm
-
B.
5cm
-
C.
10cm
-
D.
9cm
Một máy chiếu sử dụng thấu kính hội tụ có tiêu cự 10 cm tạo ảnh thật trên màn có diện tích gấp 400 lần diện tích vật. Thấu kính cách vật và màn bao nhiêu cm?
-
A.
11 cm; 440 cm.
-
B.
10,5 cm; 210 cm
-
C.
11 cm; 220 cm
-
D.
10,5 cm; 420 cm.
Một chiếc phông hình tròn, đường kính 210 cm được chiếu sáng vào buổi tối. Để tạo độ sáng dịu trên phông, một học sinh đã lắp trước đèn, cách đèn 3 cm một thấu kính phân kỳ có tiêu cự f = - 5 cm, đường kính 10 cm. Coi đèn là nguồn sáng điểm. Vị trí đặt thấu kính thế nào để ánh sáng qua thấu kính chiếu vừa vặn vào phông?
-
A.
Quang tâm thấu kính nằm trên đường vuông góc với mặt phẳng phông, đi qua tâm phông, cách phông 35,7 cm.
-
B.
Quang tâm thấu kính nằm trên đường vuông góc với mặt phẳng phông, đi qua tâm phông, cách phông 375 cm.
-
C.
Quang tâm thấu kính nằm trên đường vuông góc với mặt phẳng phông, đi qua tâm phông, cách phông 3,75 cm.
-
D.
Quang tâm thấu kính nằm trên đường vuông góc với mặt phẳng phông tại tâm phông, cách phông 37,5 cm.
Hai thấu kính được ghép đồng trục, thấu kính \({L_1}\) có tiêu cự \({f_1} = {\rm{ }}10{\rm{ }}cm\), thấu kính \({L_2}\) có tiêu cự \({f_2} = - {\rm{ }}10{\rm{ }}cm\). Khoảng cách giữa hai kính là \(a{\rm{ }} = {\rm{ }}40{\rm{ }}cm\). Phía ngoài hệ, trước \({L_1}\) có vật sáng AB vuông góc với trục chính hệ thấu kính tại A, cách \({L_1}\) \(15cm\). Ảnh cuối cùng qua hệ là
-
A.
ảnh ảo, ngược chiều vật AB, cao bằng vật AB, cách L2 5 cm.
-
B.
ảnh ảo, cùng chiều với vật AB, cao bằng vật AB, cách L2 5 cm.
-
C.
ảnh thật, ngược chiều với vật AB, cao bằng vật AB, cách L2 5 cm.
-
D.
ảnh thật, cùng chiều với vật AB, cao bằng vật AB, cách L2 5 cm.
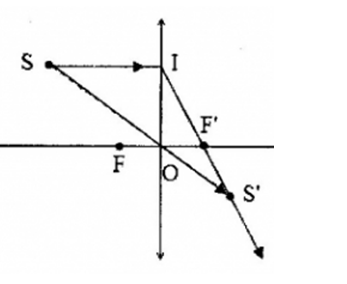
Trong hình vẽ bên, S’ là ảnh của một điểm sáng S qua một thấu kình có trục chính xx’. Nhận xét nào sau đây sai?
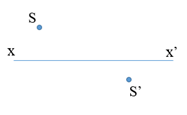
-
A.
S’ là ảnh thật
-
B.
S’ là ảnh ảo
-
C.
Giao điểm của đường thẳng nối SS’ với xx’ là quang tâm O của thấu kính
-
D.
Thấu kính trên là thấu kính hội tụ
Đặt vật AB cao 2 cm trước một thấu kính phân kỳ có tiêu cự 12 cm, cách thấu kính một khoảng 12cm thì ta thu được
-
A.
ảnh ảo A’B’, cùng chiều với vật, vô cùng lớn.
-
B.
ảnh thật A’B’, ngược chiều với vật, vô cùng lớn.
-
C.
ảnh thật A’B’, ngược chiều với vật, cao 4 cm.
-
D.
ảnh ảo A’B’, cùng chiều với vật, cao 1 cm.
Vật sáng AB đặt vuông góc với trục chính qua thấu kính cho ảnh ngược chiều cao gấp 3 lần vật và cách nó \(80cm\). Tiêu cự của thấu kính là
-
A.
\(30cm\)
-
B.
\(15cm\)
-
C.
\(20cm\)
-
D.
\(24cm\)
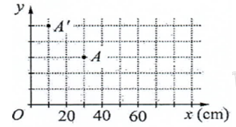
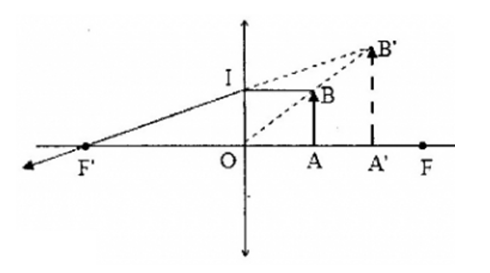
Một thấu kính mỏng được đặt sao cho trục chính trùng với trục Ox của hệ trục tọa độ vuông góc Oxy. Điểm sáng A đặt gần trục chính, trước thấu kính. A' là ảnh của A qua thấu kính (hình bên). Tiêu cự của thấu kính là

-
A.
30cm.
-
B.
60cm.
-
C.
75cm.
-
D.
12,5cm.
Một vật phẳng nhỏ \(AB\) đặt trước một thấu kính hội tụ, cho một ảnh thật cách thấu kính \(60cm\). Nếu thay thấy kính hội tụ bằng thấu kính phân kì có cùng độ lớn tiêu cự và đặt đúng vào chỗ thấu kính hội tụ thì ảnh của \(AB\) sẽ nằm cách thấu kính \(12cm\). Tiêu cự của thấu kính hội tụ là
-
A.
\(f = 30cm.\)
-
B.
\(f = 25cm.\)
-
C.
\(f = 40cm.\)
-
D.
\(f = 20cm.\)
Một thấu kính hội tụ có tiêu cự 30 cm. Vật sáng AB đặt vuông góc với trục chính của thấu kính. Ảnh của vật tạo bởi thấu kính là ảnh ảo và cách vật 40 cm. Khoảng cách từ AB đến thấu kính có giá trị gần nhất với giá trị nào sau đây?
-
A.
60 cm.
-
B.
43 cm.
-
C.
26 cm.
-
D.
10cm.
Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có độ tụ 2dp và cách thấu kính một khoảng 25cm. Khoảng cách từ ảnh A’B’ đến AB là:
-
A.
25cm
-
B.
35cm
-
C.
60cm
-
D.
50cm
Đặt vật AB trước thấu kính phân kì, ta được ảnh A’B’. Đưa vật ra xa thấu kính thêm 30 cm thì ảnh tịnh tiến 1 cm. Ảnh trước cao gấp 1,2 lần sau. Tiêu cự của thấu kính là
-
A.
-30 cm
-
B.
-40 cm
-
C.
-10 cm
-
D.
-20 cm
Thấu kính hội tụ có tiêu cự f. Khoảng cách ngắn nhất giữa vật thật và ảnh thật qua thấu kính là
-
A.
4f.
-
B.
3f.
-
C.
5f.
-
D.
6f.
Một vật sáng phẳng AB có chiều cao H đặt vuông góc với trục chính của thấu kính và ở trước thấu kính. Khi di chuyển thấu kính giữa vật và màn, có hai vị trí cho ảnh rõ nét trên màn. Các ảnh trên màn có chiều cao lần lượt là h1 và h2. Khoảng cách giữa vật sáng và màn ảnh không đổi. Chiều cao H tính theo h1 và h2 là:
-
A.
\(H = \sqrt {{h_1} + {h_2}} \)
-
B.
\(H = \sqrt {{h_1}{h_2}} \)
-
C.
\(H = \frac{{{h_1}}}{{{h_2}}}\)
-
D.
\(H = \frac{{{h_1}}}{{{h_1} + {h_2}}}\)
Vật sáng phẳng AB đặt vuông góc với trục chính của một thấu kính cho ảnh lớn gấp 3 lần vật. Khi dịch chuyển vật gần thêm một khoảng 8 cm thì thấy ảnh có độ lớn không đổi. Tính tiêu cự của thấu kính.
-
A.
10cm
-
B.
20cm
-
C.
12cm
-
D.
30cm
Một học sinh bố trí thí nghiệm theo sơ đồ như hình vẽ. Thấu kính phân kì L có tiêu cự -10 cm. Khoảng cách từ ảnh tạo bởi thấu kính đến màn có giá trị nào?
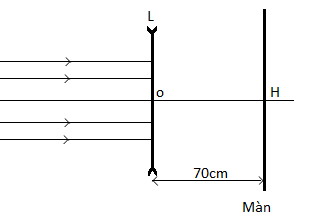
-
A.
60cm
-
B.
70cm
-
C.
80cm
-
D.
100cm
Lời giải và đáp án
Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có độ tụ 2dp và cách thấu kính một khoảng 25cm. Khoảng cách từ ảnh A’B’ đến AB là:
-
A.
25cm
-
B.
35cm
-
C.
60cm
-
D.
50cm
Đáp án : A
+ Sử dụng công thức tính độ tụ: \(D = \frac{1}{f}\)
+ Áp dụng công thức thấu kính:
\(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Khoảng cách vật ảnh: \(L = \left| {d + d'} \right|\)
Ta có:
+ Tiêu cự của thấu kính: \(f = \frac{1}{D} = \frac{1}{2} = 0,5m = 50cm\)
+ \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to d' = \frac{{df}}{{d - f}} = \frac{{25.50}}{{25 - 50}} = - 50cm\)
+ Khoảng cách vật ảnh: \(L = \left| {d + d'} \right| = \left| {25 - 50} \right| = 25cm\)
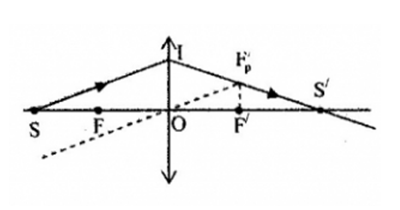
Ảnh S’ của điểm sáng S được đặt như hình là:

-
A.
-
B.
-
C.
-
D.
Đáp án : A
Vận dụng phương pháp vẽ ảnh qua thấu kính hội tụ
+ Kẻ tia tới SI bất kì
+ Kẻ trục phụ song song với SI
+ Qua F’ kẻ đường vuông góc với trục chính, cắt trục phụ tại tiêu điểm phụ Fp’
+ Tia tới song song với trục phụ thì tia ló qua tiêu điểm phụ nên tia ló qua I và Fp’, tia ló này cắt trục chính tại S. S’ là ảnh cần xác định
Chọn phương án đúng về cách vẽ ảnh A’B’ của vật sáng AB trong các trường hợp sau:
-
A.
-
B.
-
C.
-
D.
Đáp án : C
Vận dụng phương pháp vẽ ảnh qua thấu kính
Sử dụng 2 tia đặc biệt để xác định ảnh của vật qua thấu kính
A - sai vì: ảnh A’B’ là ảnh ảo
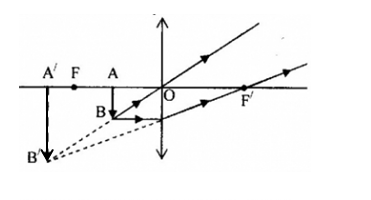
B - sai vì: tia đi qua quang tâm thì truyền thẳng
C - đúng
D - sai vì: ảnh A’B’ là ảnh ảo
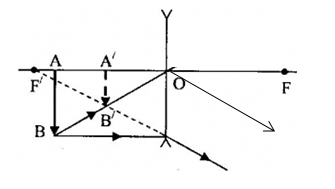
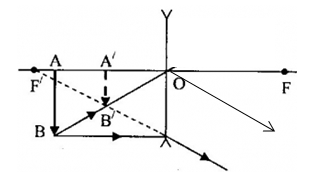
xy là trục chính của thấu kính, AB là vật thật, A’B’ là ảnh

Hãy cho biết A’B’ là ảnh gì?
-
A.
ảnh ảo
-
B.
ảnh thật
-
C.
ảnh đối xứng
-
D.
không xác định được
Đáp án: A
Sử dụng tính chất vật - ảnh
Ta có: AB và A’B’ cùng chiều => ảnh và vật trái tính chất
Vì AB là vật thật => ảnh A’B’ là ảnh ảo
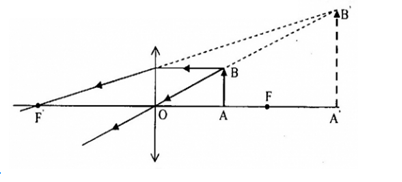
thấu kính thuộc loại nào và vật được đặt trước hay sau thấu kính?
-
A.
Thấu kính hội tụ và vật đặt trước thấu kính
-
B.
Thấu kính hội tụ và vật đặt sau thấu kính
-
C.
Thấu kính phân kì và vật đặt trước thấu kính
-
D.
Thấu kính phân kì và vật đặt sau thấu kính
Đáp án: B
+ Sử dụng tính chất vật - ảnh qua thấu kính
+ Vẽ ảnh của vật qua thấu kính
+ Ta có, ảnh A’B’ lớn hơn vật AB nên thấu kính là thấu kính hội tụ
+ Xác định vị trí vật:
- Vì điểm vật, điểm ảnh, quang tâm thẳng hàng => nối BB’ thì cắt trục chính xy tại $O$.
- Qua $O$ dựng thấu kính hội tụ.
- Từ B kẻ tia tới BI // xy thì tia ló qua I có đường kéo dài qua B’ cắt trục chính tại F’. Lấy F đối xứng với F’ qua O.
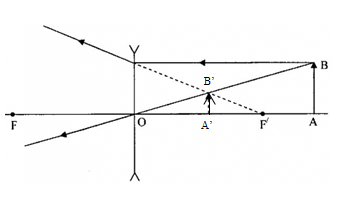
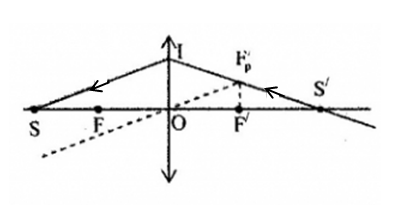
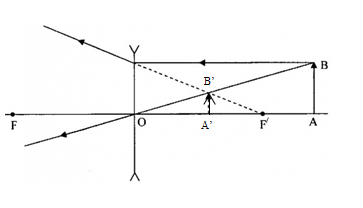
Trong hình sau, S- là điểm vật thật, S’- là điểm ảnh, xy - là trục chính thấu kính.

Hãy cho biết S’ là ảnh gì và thấu kính thuộc loại nào?
-
A.
ảnh ảo và thấu kính phân kỳ
-
B.
ảnh thật và thấu kính hội tụ
-
C.
ảnh ảo và thấu kính hội tụ
-
D.
ảnh thật và thấu kính phân kỳ
Đáp án: B
Sử dụng tính chất ảnh - vật qua thấu kính
Ta có:
+ Vì S’ và S ở khác phía trục chính nên S và S’ cùng tính chất => S’ là ảnh thật.
+ Vật thật cho ảnh thật => thấu kính là thấu kính hội tụ
Gọi d là khoảng cách từ S đến thấu kính, d nằm trong khoảng nào?
-
A.
$d < {\text{OF}}$
-
B.
$d > {\text{OF}}$
-
C.
$d = {\text{OF}}$
-
D.
\({\text{0 < d < OF}}\)
Đáp án: B
Phương pháp vẽ ảnh
+ Vẽ hai đường đặc biệt
+ Giao của hai đường
+ Vì điểm vật, điểm ảnh và quang tâm O thẳng hàng nên nối SS’ cắt trục chính tại điểm O là quang tâm.
+ Qua O dựng thấu kính hội tụ vuông góc với trục chính.
+ Kẻ tia SI // xy thì tia ló qua IS’, cắt xy tại F’. Lấy F đối xứng với F’ qua O.
=> điểm S nằm ngoài tiêu cực, d > OF
Cho thấu kính hội tụ có tiêu cự f = 10cm. Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính, cách thấu kính 30cm. Tính chất của ảnh và số phóng đại ảnh là:
-
A.
ảnh ảo cùng chiều với vật, k = 0,5
-
B.
ảnh thật cùng chiều với vật, k = -0,5
-
C.
ảnh ảo ngược chiều với vật, k = 0,5
-
D.
ảnh thật ngược chiều với vật, k = -0,5
Đáp án : D
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính số phóng đại: \(k = - \frac{{d'}}{d}\)
Ta có:
+ \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to d' = \frac{{df}}{{d - f}} = \frac{{30.10}}{{30 - 10}} = 15cm > 0\)
=> ảnh là ảnh thật và cách thấu kính một đoạn \(d' = 15cm\)
+ Số phóng đại của ảnh: $k = - \frac{{d'}}{d} = - \frac{{15}}{{30}} = - \frac{1}{2}$
Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ và cách thấu kính 10cm. Nhìn qua thấu kính thấy một ảnh cùng chiều và cao gấp 3 lần vật. Tiêu cự của thấu kính có giá trị là:
-
A.
10cm
-
B.
25cm
-
C.
15cm
-
D.
5cm
Đáp án : C
+ Sử dụng công thức xác định số phóng đại: \(k = - \frac{{d'}}{d}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Ta có, vật thật qua thấu kính hội tụ cho ảnh cùng chiều với vật thì đó là ảnh ảo
\( \to d' < 0 \to k > 0\)
+ Số phóng đại \(k = - \frac{{d'}}{d} = 3\) (1)
+ Mặt khác, ta có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\) (2)
Từ (1) và (2), ta suy ra: \(\left\{ \begin{array}{l}d' = - 3{\rm{d}}\\\frac{1}{f} = \frac{1}{d} - \frac{1}{{3{\rm{d}}}} = \frac{2}{{3d}}\end{array} \right. \to f = \frac{{3{\rm{d}}}}{2} = \frac{{3.10}}{2} = 15cm\)

Đặt một thấu kính cách một trang sách 20cm, nhìn qua thấu kính thấy ảnh của dòng chữ cùng chiều với dòng chữ nhưng cao bằng nửa dòng chữ thật. Thấu kính thuộc loại gì và tiêu cự có giá trị là bao nhiêu?
-
A.
Thấu kính hội tụ, f = 20cm
-
B.
Thấu kính phân kì, f = -20cm
-
C.
Thấu kính hội tụ, f =10cm
-
D.
Thấu kính phân kì, f = -10cm
Đáp án : B
+ Sử dụng tính chất vật - ảnh
+ Sử dụng công thức tính số phóng đại: \(k = - \frac{{d'}}{d}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Ta có:
+ Ảnh cùng chiều với vật thật => đó là ảnh ảo
Vật thật cho ảnh ảo nhỏ hơn vật => đó là thấu kính phân kì
+ Vì là ảnh ảo nên \(k > 0 \to k = \frac{1}{2}\)
\( \to k = - \frac{{d'}}{d} = \frac{1}{2} \to d' = - \frac{1}{{2{\rm{d}}}}\)
+ Mặt khác, ta có:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \leftrightarrow \frac{1}{f} = \frac{1}{d} - \frac{2}{{\rm{d}}} = - \frac{1}{d}\\ \to f = - {\rm{d}} = - 20cm\end{array}\)
Vật \(AB = 10cm\) là một đoạn thẳng song song với trục chính của một thấu kính hội tụ mỏng tiêu cự \(f = 20cm\). B gần thấu kính và cách thấu kính \(30cm\). Khoảng cách \(AB\) tới trục chính của thấu kính là \(h = 3cm\). Độ lớn của ảnh là:
-
A.
12cm
-
B.
40cm
-
C.
20,2cm
-
D.
24,6cm
Đáp án : C
+ Vẽ ảnh của vật qua thấu kính
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính hệ số phóng đại: \(k = - \frac{{d'}}{d}\)
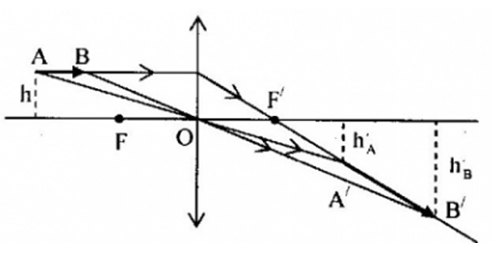
Ta có:
+ Ảnh \(A'B'\) nằm dọc tia ló ứng với tia truyền dọc theo \(AB\)
+ \(\left\{ \begin{array}{l}{d_A} = 30 + 10 = 40cm\\{d_B} = 30cm\end{array} \right.\)
Áp dụng công thức thấu kính: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
Ta suy ra: \(\left\{ \begin{array}{l}{d_A}' = \dfrac{{{d_A}f}}{{{d_A} - f}} = \dfrac{{40.20}}{{40 - 20}} = 40cm\\{d_B}' = \dfrac{{{d_B}f}}{{{d_B} - f}} = \dfrac{{30.20}}{{30 - 20}} = 60cm\end{array} \right.\)
+ Ta suy ra: \(\left\{ \begin{array}{l}\dfrac{{{h_A}}}{h} = \left| { - \dfrac{{{d_A}'}}{{{d_A}}}} \right| = \dfrac{{40}}{{40}} = 1 \to {h_A} = h = 3cm\\\dfrac{{{h_B}}}{h} = \left| { - \dfrac{{{d_B}'}}{{{d_B}}}} \right| = \dfrac{{60}}{{30}} = 2 \to {h_B} = 2h = 6cm\end{array} \right.\)
Ảnh \(A'B'\) là ảnh thật, nghiêng góc với trục chính:
Độ lớn của ảnh:
$\begin{gathered}
A'B' = \sqrt {{{\left( {{d_B}' - {d_A}'} \right)}^2} + {{\left( {{h_B} - {h_A}} \right)}^2}} \hfill \\
= \sqrt {{{\left( {60 - 40} \right)}^2} + {{\left( {6 - 3} \right)}^2}} = 20,2cm \hfill \\
\end{gathered} $
Một thấu kính phân kì có tiêu cự f = -30cm. Vật sáng AB là một đoạn thẳng đặt vuông góc trục chính của thấu kính cho ảnh cách vật 15cm. Vị trí của vật là:
-
A.
30cm
-
B.
-15cm
-
C.
15cm
-
D.
-30cm
Đáp án : A
+ Sử dụng công thức tính khoảng cách vật ảnh:
\(L = d + d'\)
+ Sử dụng công thức thấu kính:
\(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Vật thật qua thấu kính phân kì cho ảnh ảo cùng phía vật so với thấu kính và ảnh ở gần thấu kính hơn vật nên:
\(d > d' \to L = d + d' > 0 \to d + d' = 15cm\)
Ta có:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to d' = \frac{{df}}{{d - f}}\\ \to L = d + d' = d + \frac{{df}}{{d - f}} = 15\\ \leftrightarrow df = \left( {15 - d} \right)\left( {d - f} \right)\\ \leftrightarrow {d^2} - 15d + 15f = 0\\ \leftrightarrow {d^2} - 15d + 15.\left( { - 30} \right) = 0\\ \leftrightarrow {d^2} - 15{\rm{d}} - 450 = 0\\ \to \left[ \begin{array}{l}d = 30cm\\d = - 15cm(loai)\end{array} \right.\end{array}\)
(\(d = - 15cm\): loại vì vật thật)
Vật sáng AB đặt vuông góc với trục chính của một thấu kính phẳng lồi bằng thủy tinh chiết suất n =1,5 bán kính mặt lồi bằng 10cm , cho ảnh rõ nét trên màn đặt cách vật một khoảng L. Khoảng cách ngắn nhất của L là:
-
A.
40cm
-
B.
20cm
-
C.
80cm
-
D.
60cm
Đáp án : C
+ Sử dụng công thức tính tiêu cự của thấu kính:
\(\frac{1}{f} = \left( {n - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\)
+ Sử dụng công thức tính khoảng cách vật - ảnh:
\(L = d + d'\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Áp dụng hệ thức giải phương trình bậc 2
Ta có:
+ Tiêu cự của thấu kính:
\(\begin{array}{l}\frac{1}{f} = \left( {n - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\\ = \left( {1,5 - 1} \right)\left( {\frac{1}{{10}} + \frac{1}{\infty }} \right) = \frac{1}{{20}}\\ \to f = 20cm\end{array}\)
+ Vì ảnh hứng trên màn là ảnh thật nên \(d' > 0 \to L = d + d'\) (1)
+ \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to d = \frac{{d'f}}{{d' - f}}\) (2)
Thế (2) vào (1), ta được: \(\)
\( \leftrightarrow L\left( {d' - f} \right) = d{'^2} \leftrightarrow d{'^2} - L{\rm{d}}' + fL = 0\) (3)
Vì trên màn thu được ảnh rõ nét nên phương trình (3) phải có nghiệm hay \(\Delta \ge 0\)
\(\begin{array}{l}\Delta = {b^2} - 4{\rm{a}}c = {L^2} - 4fL \ge 0\\ \to L \ge 4f \to {L_{\min }} = 4f = 4.20 = 80cm\end{array}\)
Đặt một vật sáng AB trước một thấu kính hội tụ có tiêu cự f =20cm. Cách vật AB một đoạn 90cm, người ta đặt một màn hứng. Ta phải đặt thấu kính ở vị trí cách vật bao nhiêu thì thu được ảnh rõ nét trên màn?
-
A.
30cm hoặc 60cm
-
B.
20cm hoặc 50cm
-
C.
25cm hoặc 75cm
-
D.
10cm hoặc 40cm
Đáp án : A
+ Sử dụng công thức tính khoảng cách vật - ảnh: \(L = d + d'\)
+ Sử dụng công thức thấu kính:
\(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Vì ảnh hứng trên màn nên: \(L = d + d' = 90cm\) (1)
+ Theo công thức thấu kính, ta có: $\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to d' = \frac{{df}}{{d - f}}$ (2)
Thế (2) vào (1), ta được:
\(\begin{array}{l}d + \frac{{df}}{{d - f}} = L \leftrightarrow {d^2} - Ld + Lf = 0\\ \leftrightarrow {d^2} - 90{\rm{d}} + 90.20 = 0\\ \to \left[ \begin{array}{l}d = 30cm\\d = 60cm\end{array} \right.\end{array}\).
Một vật sáng AB cho ảnh thật qua một thấu kính hội tụ, ảnh này hứng trên một màn E đặt cách vật một khoảng 180cm, ảnh thu được cao bằng 1/5 vật. Tiêu cự của thấu kính có giá trị:
-
A.
15cm
-
B.
10cm
-
C.
5cm
-
D.
25cm
Đáp án : D
+ Sử dụng biểu thức xác định hệ số phóng đại: \(k = - \frac{{d'}}{d}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính khoảng cách vật - ảnh: \(L = d + d'\)
+ Vì vật thật nên: \(d' > 0 \to \left\{ \begin{array}{l}k < 0\\L > 0\end{array} \right. \to \left\{ \begin{array}{l}k = - \frac{1}{5}\\L = d + d' = 180cm\end{array} \right.\)
+ \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to d' = \frac{{df}}{{d - f}}\)
\(\begin{array}{l} \to k = - \frac{{d'}}{d} = - \frac{{\frac{{df}}{{d - f}}}}{d} = \frac{f}{{f - d}} = - \frac{1}{5}\\ \to d = 6f\end{array}\)
+ Lại có: \(L = d + d' = 180cm\)
\(\begin{array}{l} \to d + \frac{{df}}{{d - f}} = 180\\ \leftrightarrow 6f + \frac{{6{f^2}}}{{6f - f}} = 180\\ \to f = 25cm\end{array}\)
Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L = 72cm. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính, người ta tìm được vị trí của thấu kính cho ảnh rõ nét trên màn. Hai vị trí này cách nhau 48cm, tính tiêu cự của thấu kính?
-
A.
5cm
-
B.
10cm
-
C.
15cm
-
D.
20cm
Đáp án : B
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính khoảng cách vật - ảnh: \(L = d + d'\)
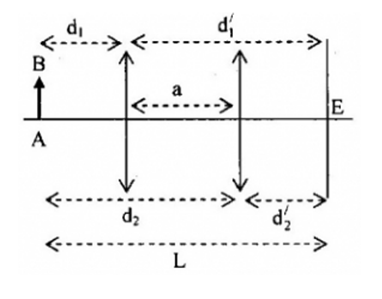
Theo tính thuận nghịch của chiều truyền ánh sáng, ta có: \(\left\{ \begin{array}{l}{d_1} = {d_2}'\\{d_2} = {d_1}'\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}{d_1} + {d_1}' = L\\{d_1}' - {d_1} = a\end{array} \right. \to \left\{ \begin{array}{l}{d_1} = \frac{{L - a}}{2}\\{d_1}' = \frac{{L + a}}{2}\end{array} \right.\)
Mặt khác, ta có: \(\begin{array}{l}\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{{d_1}'}} = \frac{2}{{L - a}} + \frac{2}{{L + a}}\\ \leftrightarrow \frac{1}{f} = \frac{2}{{72 - 48}} + \frac{2}{{72 + 48}}\\ \to f = 10cm\end{array}\)
Một thấu kính có dạng một mặt phẳng và một mặt cầu làm bằng thủy tinh có chiết suất n =1,5. Đặt trong không khí, một chùm sáng tới song song với trục chính cho chùm tia ló hội tụ tại điểm phía sau thấu kính, cách thấu kính 12cm. Bán kính của mặt cầu có giá trị là:
-
A.
2,5cm
-
B.
5cm
-
C.
3cm
-
D.
6cm
Đáp án : D
+ Sử dụng tính chất của các chùm tia xác định loại thấu kính
+ Sử dụng công thức:
\(\frac{1}{f} = \left( {n - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\)
+ Vì chùm tia ló hội tụ nên đó là thấu kính hội tụ => mặt cầu là mặt lồi
+ Ta có: \(f = 12cm\) theo đề bài
Lại có: \(\frac{1}{f} = \left( {n - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\)
\( \to \frac{1}{{12}} = \left( {1,5 - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{\infty }} \right) \to {R_1} = 6cm\)
Một thấu kính thủy tinh có chiết suất n =1,5 đặt trong không khí có độ tụ 8dp. Khi nhúng thấu kính vào một chất lỏng nó trở thành một thấu kính phân kì có tiêu cự 1m. Chiết suất của chất lỏng là:
-
A.
1,2
-
B.
1
-
C.
1,6
-
D.
1,7
Đáp án : C
Sử dụng biểu thức: \(D = \frac{1}{f} = \left( {\frac{n}{{{n_{mt}}}} - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\)
+ Khi đặt trong không khí thì:
\({D_1} = 8dp = \left( {\frac{n}{{{n_{mt}}}} - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right) = \left( {1,5 - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\,(1)\)
+ Khi đặt thấu kính trong chất lỏng có chiết suất \({n_{mt}}=n'\) thì:
\({D_2} = \frac{1}{{{f_2}}} = \left( {\frac{n}{{{n_{mt}}}} - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right) = \left( {\frac{{1,5}}{{n'}} - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\)
theo đầu bài ta có khi đặt trong chất lỏng thì nó trở thành thấu kính phân kì có tiêu cự 1m
\( \to {f_2} = - 1m \to {D_2} = - 1dp = \left( {\frac{{1,5}}{{n'}} - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\) (2)
Từ (1) và (2), ta có: \(\frac{{{D_1}}}{{{D_2}}} = - 8 = \frac{{\left( {1,5 - 1} \right)}}{{\left( {\frac{{1,5}}{{n'}} - 1} \right)}} \to \left( {\frac{{1,5}}{{n'}} - 1} \right) = - \frac{1}{{16}} \to n' = 1,6\)
Một thấu kính hai mặt lồi cùng bán kính R, khi đặt trong không khí nó có tiêu cự f = 30cm. Nhúng chìm thấu kính vào một bể nước, cho trục chính của nó thẳng đứng rồi cho một chùm sáng song song rọi thẳng đứng từ trên xuống thì thấy điểm hội tụ cách thấu kính 80cm. R = ? Biết chiết suất của nước là 4/3.
-
A.
20cm
-
B.
40cm
-
C.
25cm
-
D.
35cm
Đáp án : B
Sử dụng biểu thức: \(\frac{1}{f} = \left( {\frac{n}{{{n_{mt}}}} - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\)
+ Khi đặt thấu kính trong không khí thì:
\(\frac{1}{f} = \left( {\frac{n}{{{n_{mt}}}} - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right) \leftrightarrow \frac{1}{{30}} = \left( {n - 1} \right)\left( {\frac{2}{R}} \right)\) (1)
+ Khi đặt thấu kính trong nước thì điểm hội tụ cách thấu kính \(80cm\) nên
\(f' = 80cm\)
Ta có:
\(\frac{1}{{f'}} = \left( {\frac{n}{{{n_{mt}}}} - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right) \leftrightarrow \frac{1}{{80}} = \left( {\frac{n}{{\frac{4}{3}}} - 1} \right)\left( {\frac{2}{R}} \right)\) (2)
Từ (1) và (2), ta có: \(\frac{{f'}}{f} = \frac{{80}}{{30}} = \frac{{n - 1}}{{\frac{n}{{\frac{4}{3}}} - 1}} \to n = \frac{5}{3}\)
Thay n=5/3 vào (1) ta được: \(\frac{1}{{30}} = \left( {\frac{5}{3} - 1} \right)\left( {\frac{2}{R}} \right) \to R = 40cm\)
Vật sáng AB đặt song song với một màn M, cách màn một đoạn L = 45 cm. Giữa vật và màn có một thấu kính hội tụ song song với vật và màn, trục chính của thấu kính đi qua A. Giữ cố định vật và màn, di chuyển thấu kính giữa vật và màn thì thấy có hai vị trí thấu kính cho hai ảnh trên màn, ảnh này gấp k = 4 lần ảnh kia. Tiêu cự thấu kính là
-
A.
15cm
-
B.
5cm
-
C.
10cm
-
D.
9cm
Đáp án : C
+ Sử dụng biểu thức xác định hệ số phóng đại: \(k = - \frac{{d'}}{d} = \frac{{A'B'}}{{AB}}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính khoảng cách vật - ảnh: \(L = d + d'\)
+ Khoảng cách vật và màn cố định, giữa vật và màn có hai vị trí thấu kính cho ảnh rõ nét trên màn thì theo nguyên lý về tính thuận nghịch của sự truyền ánh sáng, hai vị trí này phải có tính chất đối xứng, tức là:
\({d_1}' = {d_2}\)và \({d_2}' = {d_1}\) (1)
+ Theo giả thiết: \(k = \frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = 4\)
+ Lại có: \(k = \frac{{{A_1}{B_1}}}{{{A_2}{B_2}}} = \frac{{\overline {{A_1}{B_1}} }}{{\overline {{A_2}{B_2}} }} = \frac{{\overline {{A_1}{B_1}} }}{{\overline {AB} }}.\frac{{\overline {AB} }}{{\overline {{A_2}{B_2}} }} = \frac{{{k_1}}}{{{k_2}}}\) (2)
+ \({k_1} = - \frac{{{d_1}'}}{{{d_1}}};{k_2} = - \frac{{{d_2}'}}{{{d_2}}}\) (3)
Từ (1); (2) và (3) ta có: \(\sqrt k = \frac{{{d_1}'}}{{{d_1}}}\)
\( \to \frac{{\sqrt k }}{{{d_1}'}} = \frac{1}{{{d_1}}}\)
Theo tính chất phân thức:
\(\frac{{\sqrt k }}{{{d_1}'}} = \frac{1}{{{d_1}}} = \frac{{\sqrt k + 1}}{L}\) (*)
+ Theo công thức thấu kính:
\(f = \frac{{{d_1}{d_1}'}}{{{d_1} + {d_1}'}} = \frac{{{d_1}{d_1}'}}{L}\) (**)
Từ (*) và (**), ta được: \(f = \frac{{L\sqrt k }}{{{{\left( {\sqrt k + 1} \right)}^2}}}\)
Thay số, được: \(f = 10cm\)
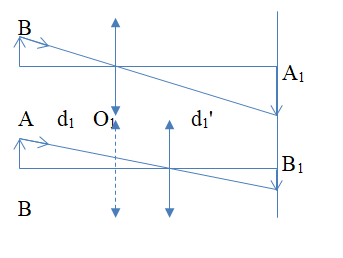
Một máy chiếu sử dụng thấu kính hội tụ có tiêu cự 10 cm tạo ảnh thật trên màn có diện tích gấp 400 lần diện tích vật. Thấu kính cách vật và màn bao nhiêu cm?
-
A.
11 cm; 440 cm.
-
B.
10,5 cm; 210 cm
-
C.
11 cm; 220 cm
-
D.
10,5 cm; 420 cm.
Đáp án : B
+ Sử dụng biểu thức xác định hệ số phóng đại: \(k = - \frac{{d'}}{d} = \frac{{A'B'}}{{AB}}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính khoảng cách vật - ảnh: \(L = d + d'\)
+ Gọi k là số phóng đại ảnh của thấu kính; \({S_v} = {\rm{ }}a{\rm{ }}x{\rm{ }}b\) là diện tích vật; \({S_a} = {\rm{ }}a'{\rm{ }}x{\rm{ }}b'\) là diện tích ảnh trên màn.
+ Theo định nghĩa: \(a'{\rm{ }} = {\rm{ }}\left| k \right|a;{\rm{ }}b'{\rm{ }} = {\rm{ }}\left| k \right|b\)
\( \to {S_a} = {k^2}\left( {a{\rm{ }}x{\rm{ }}b} \right) = {k^2}{S_v} \to \left| k \right| = \sqrt {\frac{{{S_a}}}{{{S_v}}}} \)
+ Thay số, lưu ý ảnh thật ngược chiều với vật, ta được k = - 20.
+ Vận dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\) và \(k = - \frac{{d'}}{d}\)
\( \to d = \frac{{f\left( {k - 1} \right)}}{k}\)
Thay số, được d = 10,5 cm; d' = 210 cm
Một chiếc phông hình tròn, đường kính 210 cm được chiếu sáng vào buổi tối. Để tạo độ sáng dịu trên phông, một học sinh đã lắp trước đèn, cách đèn 3 cm một thấu kính phân kỳ có tiêu cự f = - 5 cm, đường kính 10 cm. Coi đèn là nguồn sáng điểm. Vị trí đặt thấu kính thế nào để ánh sáng qua thấu kính chiếu vừa vặn vào phông?
-
A.
Quang tâm thấu kính nằm trên đường vuông góc với mặt phẳng phông, đi qua tâm phông, cách phông 35,7 cm.
-
B.
Quang tâm thấu kính nằm trên đường vuông góc với mặt phẳng phông, đi qua tâm phông, cách phông 375 cm.
-
C.
Quang tâm thấu kính nằm trên đường vuông góc với mặt phẳng phông, đi qua tâm phông, cách phông 3,75 cm.
-
D.
Quang tâm thấu kính nằm trên đường vuông góc với mặt phẳng phông tại tâm phông, cách phông 37,5 cm.
Đáp án : D
+ Sử dụng hệ thức lượng trong tam giác
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Thấu kính phân kỳ tạo ảnh ảo của đèn, ảnh này gần thấu kính hơn đèn.
+ Ánh sáng từ đèn truyền qua thấu kính đến màn coi như phát ra từ ảnh của đèn tạo bởi thấu kính.
+ Đường truyền ánh sáng đến màn được thể hiện như hình vẽ.
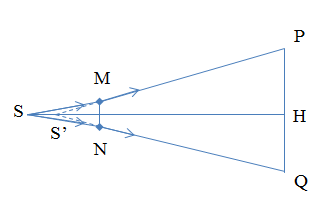
+ Ta có tam giác S'MN đồng dạng với tam giác S'PQ:
\(\frac{{MN}}{{PQ}} = \frac{{|d'| + OH}}{{|d'|}}\)
Thay số, ta được:
\(OH{\rm{ }} = {\rm{ }}20\left| {d'} \right|\) (1)
+ Theo công thức xác định vị trí ảnh:
\(d' = \frac{{df}}{{d - f}} = \frac{{3.( - 5)}}{{3 + 5}} = - \frac{{15}}{8}cm\) (2)
Từ (1) và (2), ta được: \(OH{\rm{ }} = {\rm{ }}37,5{\rm{ }}cm\)
Hai thấu kính được ghép đồng trục, thấu kính \({L_1}\) có tiêu cự \({f_1} = {\rm{ }}10{\rm{ }}cm\), thấu kính \({L_2}\) có tiêu cự \({f_2} = - {\rm{ }}10{\rm{ }}cm\). Khoảng cách giữa hai kính là \(a{\rm{ }} = {\rm{ }}40{\rm{ }}cm\). Phía ngoài hệ, trước \({L_1}\) có vật sáng AB vuông góc với trục chính hệ thấu kính tại A, cách \({L_1}\) \(15cm\). Ảnh cuối cùng qua hệ là
-
A.
ảnh ảo, ngược chiều vật AB, cao bằng vật AB, cách L2 5 cm.
-
B.
ảnh ảo, cùng chiều với vật AB, cao bằng vật AB, cách L2 5 cm.
-
C.
ảnh thật, ngược chiều với vật AB, cao bằng vật AB, cách L2 5 cm.
-
D.
ảnh thật, cùng chiều với vật AB, cao bằng vật AB, cách L2 5 cm.
Đáp án : A
+ Vẽ ảnh của vật qua hai thấu kính
+ Sử dụng công thức thấu kính: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
+ Sử dụng biểu thức xác định hệ số phóng đại: \(k = - \dfrac{{d'}}{d} = \dfrac{{A'B'}}{{AB}}\)
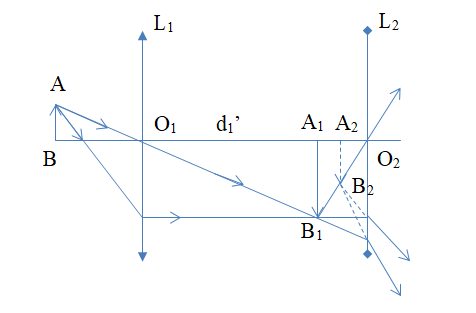
+ Qua \({L_1}\) vật \(AB\) có ảnh \({A_1}{B_1}\) cách \({L_1}\) là:
\({d_1}' = \dfrac{{{d_1}{f_1}}}{{{d_1} - {f_1}}} = \dfrac{{15.10}}{{15 - 10}} = 30cm\)
Số phóng đại \({k_1} = - \dfrac{{{d_1}'}}{{{d_1}}} = - \dfrac{{30}}{{15}} = - 2\).
+ Hình vẽ cho thấy, \({A_1}{B_1}\) cách thấu kính \({L_2}\) một đoạn:
\({d_2} = {\rm{ }}a{\rm{ }} - {d_1}'{\rm{ }} = {\rm{ }}40{\rm{ }} - {\rm{ }}30{\rm{ }} = {\rm{ }}10{\rm{ }}cm\)
+ Ánh sáng truyền qua \({L_1}\) hội tụ tại \({A_1}{B_1}\) rồi lại truyền tiếp tới \({L_2}\).
Do vậy \({A_1}{B_1}\) lại là vật sáng đối với \({L_2}\)
+ Vận dụng công thức thấu kính với \({L_2}\), ta được:
\({d_2}' = \dfrac{{{d_2}{f_2}}}{{{d_2} - {f_2}}} = \dfrac{{10.( - 10)}}{{10 + 10}} = - 5cm\)
\({k_2} = - \dfrac{{{d_2}'}}{{{d_2}}} = \dfrac{1}{2}\)
+ Số phóng đại ảnh của hệ thấu kính:
\(k = \dfrac{{\overline {{A_2}{B_2}} }}{{\overline {AB} }} = \dfrac{{\overline {{A_2}{B_2}} }}{{\overline {{A_1}{B_1}} }}.\dfrac{{\overline {{A_1}{B_1}} }}{{\overline {AB} }} = {k_2}.{k_1}\)
\(k = - 1\)
+ Vậy ảnh cuối cùng của hệ là ảnh ảo, cao bằng vật, ngược chiều với vật, cách \({L_2}\) một đoạn \(5cm\)
Trong hình vẽ bên, S’ là ảnh của một điểm sáng S qua một thấu kình có trục chính xx’. Nhận xét nào sau đây sai?
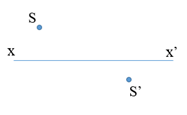
-
A.
S’ là ảnh thật
-
B.
S’ là ảnh ảo
-
C.
Giao điểm của đường thẳng nối SS’ với xx’ là quang tâm O của thấu kính
-
D.
Thấu kính trên là thấu kính hội tụ
Đáp án : B
Áp dụng đường truyền của tia sáng qua quang tâm tìm quang tâm O, từ đó xác định loại thấu kính và tính chất ảnh
Áp dụng đường truyền của tia sáng qua quang tâm
\( \Rightarrow \) Giao điểm của đường thẳng SS’ với xx’ là quang tâm O
\( \Rightarrow \) Ảnh S’ là ảnh thật và thấu kính trên là thấu kính hội tụ
=> Phương án B - sai
Đặt vật AB cao 2 cm trước một thấu kính phân kỳ có tiêu cự 12 cm, cách thấu kính một khoảng 12cm thì ta thu được
-
A.
ảnh ảo A’B’, cùng chiều với vật, vô cùng lớn.
-
B.
ảnh thật A’B’, ngược chiều với vật, vô cùng lớn.
-
C.
ảnh thật A’B’, ngược chiều với vật, cao 4 cm.
-
D.
ảnh ảo A’B’, cùng chiều với vật, cao 1 cm.
Đáp án : D
Áp dụng công thức thấu kính:
\(\left\{ \begin{array}{l}
\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\\
k = \frac{{A'B'}}{{AB}} = - \frac{{d'}}{d}
\end{array} \right.\)
Áp dụng công thức thấu kính ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\\
k = - \frac{{d'}}{d}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
d' = \frac{{df}}{{d - f}}\\
k = \frac{{A'B'}}{{AB}} = - \frac{{d'}}{d}
\end{array} \right.\\
\Leftarrow \left\{ \begin{array}{l}
d' = \frac{{12.( - 12)}}{{12 - ( - 12)}} = - 6cm\\
k = - \frac{{ - 6}}{{12}} = \frac{1}{2} \Rightarrow A'B' = 2.\frac{1}{2} = 1cm
\end{array} \right.
\end{array}\)
Vậy ảnh thu được là ảnh ảo, cùng chiều với vật và cao 1cm.
Vật sáng AB đặt vuông góc với trục chính qua thấu kính cho ảnh ngược chiều cao gấp 3 lần vật và cách nó \(80cm\). Tiêu cự của thấu kính là
-
A.
\(30cm\)
-
B.
\(15cm\)
-
C.
\(20cm\)
-
D.
\(24cm\)
Đáp án : B
Công thức thấu kính: \(\left\{ \begin{array}{l}\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}\\k = - \dfrac{{d'}}{d} = \dfrac{{\overline {A'B'} }}{{\overline {AB} }}\end{array} \right.\)
Ảnh ngược chiều cao gấp ba lần vật:
\(k = - \dfrac{{d'}}{d} = \dfrac{{\overline {A'B'} }}{{\overline {AB} }} = - 3 \Rightarrow d' = 3d\,\,\,\left( 1 \right)\)
Ảnh cách vật 80cm: \(d + d' = 80cm\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \(\left\{ \begin{array}{l}d' = 3d\\d + d' = 80cm\end{array} \right. \Rightarrow \left\{ \begin{array}{l}d = 20cm\\d' = 60cm\end{array} \right.\)
Áp dụng công thức thấu kính ta có:
\(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{{20}} + \dfrac{1}{{60}} = \dfrac{1}{{15}} \Rightarrow f = 15cm\)
Một thấu kính mỏng được đặt sao cho trục chính trùng với trục Ox của hệ trục tọa độ vuông góc Oxy. Điểm sáng A đặt gần trục chính, trước thấu kính. A' là ảnh của A qua thấu kính (hình bên). Tiêu cự của thấu kính là


-
A.
30cm.
-
B.
60cm.
-
C.
75cm.
-
D.
12,5cm.
Đáp án : C
Công thức thấu kính : \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
Từ đồ thị ta có : \(\left\{ \begin{array}{l}d + d' = - 20\\k = - \dfrac{{d'}}{d} = \dfrac{5}{3} \Leftrightarrow 5d + 3d' = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}d = 30cm\\d' = - 50cm\end{array} \right.\)
Tiêu cự của thấu kính được xác định bởi công thức:
\(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{{30}} + \dfrac{1}{{\left( { - 50} \right)}} = \dfrac{1}{{75}} \Rightarrow f = 75cm\)
Một vật phẳng nhỏ \(AB\) đặt trước một thấu kính hội tụ, cho một ảnh thật cách thấu kính \(60cm\). Nếu thay thấy kính hội tụ bằng thấu kính phân kì có cùng độ lớn tiêu cự và đặt đúng vào chỗ thấu kính hội tụ thì ảnh của \(AB\) sẽ nằm cách thấu kính \(12cm\). Tiêu cự của thấu kính hội tụ là
-
A.
\(f = 30cm.\)
-
B.
\(f = 25cm.\)
-
C.
\(f = 40cm.\)
-
D.
\(f = 20cm.\)
Đáp án : D
Sử dụng công thức thấu kính: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
Gọi \(d\) là khoảng cách từ vật đến thấu kính
\({d_1}'\) là khoảng cách từ ảnh của vật qua thấu kính hội tụ đến thấu kính
\({d_2}'\) là khoảng cách từ ảnh của vật qua thấu kính phân kì đến thấu kính
Ta có:
+ Khi dùng thấu kính hội tụ: \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{{d_1}'}} \Leftrightarrow \dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{60}}\) (1)
+ Khi dùng thấu kính phân kì: \(\dfrac{1}{{ - f}} = \dfrac{1}{d} + \dfrac{1}{{{d_2}'}} \Leftrightarrow \dfrac{1}{{ - f}} = \dfrac{1}{d} + \dfrac{1}{{ - 12}}\) (2)
Lấy \(\left( 1 \right) - \left( 2 \right)\) ta được:
\(\begin{array}{l}\dfrac{2}{f} = \dfrac{1}{{60}} + \dfrac{1}{{12}}\\ \Rightarrow f = 20cm\end{array}\)
Một thấu kính hội tụ có tiêu cự 30 cm. Vật sáng AB đặt vuông góc với trục chính của thấu kính. Ảnh của vật tạo bởi thấu kính là ảnh ảo và cách vật 40 cm. Khoảng cách từ AB đến thấu kính có giá trị gần nhất với giá trị nào sau đây?
-
A.
60 cm.
-
B.
43 cm.
-
C.
26 cm.
-
D.
10cm.
Đáp án : C
Công thức thấu kính: \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}\)
Khoảng cách giữa ảnh và vật là: \(\left| {d + d'} \right|\)
Vật thật: d > 0; Ảnh thật: d’ > 0; Ảnh ảo: d’ < 0
Tiêu cự của kính: f = 30cm
Công thức thấu kính: \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}\)
Ảnh của vật tạo bởi thấu kính là ảnh ảo và cách vật là 40cm. Ta có:
\(\left| {d + d'} \right| = 40cm \Rightarrow \left[ \begin{array}{l}d + d' = 40cm\\d + d' = - 40cm\end{array} \right.\)
TH1: \(d + d' = 40cm \Rightarrow d' = 40 - d\)
Thay vào công thức thấu kính ta có:
\(\dfrac{1}{d} + \dfrac{1}{{40 - d}} = \dfrac{1}{{30}} \Rightarrow d = - 30cm\,\,\left( {loai} \right)\)
TH2: \(d + d' = - 40cm \Rightarrow d' = - 40 - d\)
Thay vào công thức thấu kính ta có:
\(\dfrac{1}{d} - \dfrac{1}{{40 + d}} = \dfrac{1}{{30}} \Rightarrow d = 20cm\,\,\left( {t/m} \right)\)
Khoảng cách từ AB đến thấu kính có giá trị gần nhất với giá trị 26cm.
Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có độ tụ 2dp và cách thấu kính một khoảng 25cm. Khoảng cách từ ảnh A’B’ đến AB là:
-
A.
25cm
-
B.
35cm
-
C.
60cm
-
D.
50cm
Đáp án : A
Phương pháp:
+ Sử dụng công thức tính độ tụ: \(D = \frac{1}{f}\)
+ Áp dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Khoảng cách vật ảnh: \(L = \left| {d + d'} \right|\)
Hướng dẫn giải:
Ta có:
+ Tiêu cự của thấu kính: \(f = \frac{1}{D} = \frac{1}{2} = 0,5m = 50cm\)
+ \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to d' = \frac{{df}}{{d - f}} = \frac{{25.50}}{{25 - 50}} = - 50cm\)
+ Khoảng cách vật ảnh: \(L = \left| {d + d'} \right| = \left| {25 - 50} \right| = 25cm\)
Đặt vật AB trước thấu kính phân kì, ta được ảnh A’B’. Đưa vật ra xa thấu kính thêm 30 cm thì ảnh tịnh tiến 1 cm. Ảnh trước cao gấp 1,2 lần sau. Tiêu cự của thấu kính là
-
A.
-30 cm
-
B.
-40 cm
-
C.
-10 cm
-
D.
-20 cm
Đáp án : A
Thấu kính phân kì luôn cho ảnh ảo, cùng chiều, cùng phía với vật qua thấu kính
Ảnh luôn tịnh tiến cùng chiều với vật
Độ phóng đại của ảnh: \(k = \dfrac{{A'B'}}{{AB}} = - \dfrac{{d'}}{d} = \dfrac{f}{{f - d}}\)
Công thức thấu kính: \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}\)
Ta có công thức thấu kính: \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f} \Rightarrow d' = \dfrac{{df}}{{d - f}}\)
Độ phóng đại của ảnh ban đầu là: \({k_1} = \dfrac{f}{{f - {d_1}}}\)
Nhận xét: thấu kính phân kì luôn cho ảnh ảo, ảnh dịch chuyển cùng chiều với vật, ta có:
\({d_2}' = {d_1}' - 1\)
Dịch chuyển vật ra xa thấu kính, độ phóng đại của ảnh là:
\({k_2} = \dfrac{f}{{f - {d_2}}} = \dfrac{f}{{f - \left( {{d_1} + 30} \right)}}\)
Ảnh trước cao gấp 1,2 lần ảnh sau, ta có:
\(\begin{array}{l}\dfrac{{{k_2}}}{{{k_1}}} = 1,2 \Rightarrow \dfrac{{f - \left( {{d_1} + 30} \right)}}{{f - {d_1}}} = 1,2 \Rightarrow f - {d_1} - 30 = 1,2f - 1,2{d_1}\\ \Rightarrow 0,2{d_1} = 0,2f + 30 \Rightarrow {d_1} = f + 150 \Rightarrow {d_1} - f = 150\,\,\left( {cm} \right)\\ \Rightarrow {d_1}' = \dfrac{{{d_1}f}}{{{d_1} - f}} = = \dfrac{{f.\left( {f + 150} \right)}}{{150}}\end{array}\)
Lại có: \({d_2}' = {d_1}' - 1 = \dfrac{{{d_2}f}}{{{d_2} - f}} = \dfrac{{f\left( {{d_1} + 30} \right)}}{{{d_1} + 30 - f}} = \dfrac{{f\left( {f + 180} \right)}}{{180}}\)
\(\begin{array}{l} \Rightarrow \dfrac{{f.\left( {f + 150} \right)}}{{150}} - 1 = \dfrac{{f\left( {f + 180} \right)}}{{180}}\\ \Rightarrow 6f\left( {f + 150} \right) - 900 = 5f\left( {f + 180} \right)\\ \Rightarrow {f^2} - 900 = 0 \Rightarrow f = \pm 30\,\,\left( {cm} \right) \Rightarrow f = - 30\,\,\left( {cm} \right)\end{array}\)
Thấu kính hội tụ có tiêu cự f. Khoảng cách ngắn nhất giữa vật thật và ảnh thật qua thấu kính là
-
A.
4f.
-
B.
3f.
-
C.
5f.
-
D.
6f.
Đáp án : A
Công thức thấu kính: \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}\)
Khoảng cách giữa vật thật và ảnh thật: \(L = d + d'\)
Bất đẳng thức Cô – si: \(a + b \ge 2\sqrt {ab} \) (dấu “=” xảy ra \( \Leftrightarrow a = b\))
Ta có công thức thấu kính:
\(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f} \Rightarrow d' = \dfrac{{df}}{{d - f}}\)
Khoảng cách giữa vật thật và ảnh thật là:
\(\begin{array}{l}L = d + d' = d + \dfrac{{df}}{{d - f}} = \dfrac{{{d^2}}}{{d - f}} = \dfrac{{\left( {{d^2} - 2df + {f^2}} \right) + \left( {2df - 2{f^2}} \right) + {f^2}}}{{d - f}}\\ \Rightarrow L = \dfrac{{{{\left( {d - f} \right)}^2} + 2f\left( {d - f} \right) + {f^2}}}{{d - f}} = \left( {d - f} \right) + \dfrac{{{f^2}}}{{d - f}} + 2f\end{array}\)
Áp dụng bất đẳng thức Cô – si, ta có:
\(\begin{array}{l}\left( {d - f} \right) + \dfrac{{{f^2}}}{{d - f}} \ge 2\sqrt {\left( {d - f} \right).\dfrac{{{f^2}}}{{d - f}}} = 2f\\ \Rightarrow {L_{\min }} = 4f \Leftrightarrow \left( {d - f} \right) = \dfrac{{{f^2}}}{{d - f}} \Rightarrow d - f = f \Rightarrow d = 2f\end{array}\)
Một vật sáng phẳng AB có chiều cao H đặt vuông góc với trục chính của thấu kính và ở trước thấu kính. Khi di chuyển thấu kính giữa vật và màn, có hai vị trí cho ảnh rõ nét trên màn. Các ảnh trên màn có chiều cao lần lượt là h1 và h2. Khoảng cách giữa vật sáng và màn ảnh không đổi. Chiều cao H tính theo h1 và h2 là:
-
A.
\(H = \sqrt {{h_1} + {h_2}} \)
-
B.
\(H = \sqrt {{h_1}{h_2}} \)
-
C.
\(H = \frac{{{h_1}}}{{{h_2}}}\)
-
D.
\(H = \frac{{{h_1}}}{{{h_1} + {h_2}}}\)
Đáp án : B
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Hệ số phóng đại k = h’/h = d’/d
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \Rightarrow d' = \frac{{df}}{{d - f}} \Rightarrow d + d' = \frac{{{d^2}}}{{d - f}} = L \Rightarrow d{}^2 - dL + fL = 0\)
Do f không đổi nên có 2 vị trí thấu kính cho ảnh rõ nét trên màn nên d là nghiệm của phương trình bậc 2 trên
\({d_1} = \frac{{d + \sqrt {{L^2} - 4fL} }}{2};{d_2} = \frac{{d - \sqrt {{L^2} - 4fL} }}{2}\)
Ta có: \(\frac{{{h_1}}}{h} = \frac{{{d_1}'}}{{{d_1}}} = \frac{f}{{{d_1} - f}};\frac{{{h_2}}}{h} = \frac{{{d_2}'}}{{{d_2}}} = \frac{f}{{{d_2} - f}} \Rightarrow \frac{{{h_1}{h_2}}}{{{h^2}}} = 1 \Rightarrow h = \sqrt {{h_1}{h_2}} \)
Vật sáng phẳng AB đặt vuông góc với trục chính của một thấu kính cho ảnh lớn gấp 3 lần vật. Khi dịch chuyển vật gần thêm một khoảng 8 cm thì thấy ảnh có độ lớn không đổi. Tính tiêu cự của thấu kính.
-
A.
10cm
-
B.
20cm
-
C.
12cm
-
D.
30cm
Đáp án : C
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Hệ số phóng đại k = h’/h = d’/d
Ảnh lớn gấp 3 lần vật nên d’ = 3d, h’ = 3h. Ta có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{3d}} = \frac{4}{{3d}} \Rightarrow f = \frac{{3d}}{4}\)
Khi dịch chuyển vật lại gần 8cm thì d1 = d – 8, ảnh có độ lớn không đổi nên h’ = 3h => d1’ = 3(d-8)
Ta có: \(\frac{1}{f} = \frac{1}{{d - 8}} + \frac{1}{{3(d - 8)}} = \frac{4}{{3d}} \Rightarrow d = 16cm \Rightarrow f = 12cm\)
Một học sinh bố trí thí nghiệm theo sơ đồ như hình vẽ. Thấu kính phân kì L có tiêu cự -10 cm. Khoảng cách từ ảnh tạo bởi thấu kính đến màn có giá trị nào?

-
A.
60cm
-
B.
70cm
-
C.
80cm
-
D.
100cm
Đáp án : C
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Theo bài ra: d = ∞ nên cho ảnh tại tiêu điểm => d’ = f = -10cm
Khoảng cách từ ảnh đến màn là 10 + 70 = 80cm
Luyện tập và củng cố kiến thức Bài 31. Mắt Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp các dạng bài tập về mắt Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 32. Kính lúp Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 33. Kính hiển vi Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 34. Kính thiên văn Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập chương 7 Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập thấu kính (phần 2) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tông hợp bài tập thấu kính (phần 1) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 28. Lăng kính - Bài tập lăng kính Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết










Danh sách bình luận