-
Chương 1. Điện tích. Điện trường
- Bài 1. Điện tích - Định luật Culông
- Bài 2. Thuyết electron và định luật bảo toàn điện tích
- Tổng hợp bài tập định luật Culông (phần 1)
- Tổng hợp bài tập định luật Culông (phần 2)
- Bài 3. Điện trường
- Bài 3. Bài tập điện trường
- Bài 4. Công của lực điện - Hiệu điện thế
- Tổng hợp bài tập công của lực điện - Hiệu điện thế
- Bài 6. Tụ điện
- Tổng hợp bài tập về tụ điện
- Tổng hợp bài tập chuyển động của điện tích trong điện trường
- Ôn tập chương 1
-
Chương 2. Dòng điện không đổi
- Bài 7. Đại cương về dòng điện không đổi - Nguồn điện
- Bài 8. Điện năng và công suất điện
- Tổng hợp bài tập tính điện trở dây dẫn, biến trở
- Bài 9. Định luật Ôm cho đoạn mạch chỉ có điện trở
- Bài 9. Định luật Ôm đối với toàn mạch - Mắc nguồn điện thành bộ
- Tổng hợp bài tập định luật Ôm
- Bài 9. Định luật Ôm cho mạch chứa tụ điện
- Ôn tập chương 2
-
Chương 3. Dòng điện trong các môi trường
-
Chương 4. Từ trường
- Bài 19. Từ trường
- Bài 20. Lực từ - Cảm ứng từ
- Bài 21. Từ trường của dòng điện trong các dây dẫn có hình dạng đặc biệt
- Bài 21. Tương tác giữa hai dòng điện song song
- Bài 21. Khung dây đặt trong từ trường đều
- Bài 22. Lực Lorenxơ
- Bài 22. Chuyển động của hạt mang điện trong từ trường đều
- Ôn tập chương 4
-
Chương 5. Cảm ứng điện từ
-
Chương 6. Khúc xạ ánh sáng
-
Chương 7. Mắt. Các dụng cụ quang
Trắc nghiệm Tổng hợp các dạng bài tập về mắt - Vật Lí 11
Đề bài
Một người bị cận thị có khoảng cách từ thể thuỷ tinh đến điểm cực cận là \(O{C_C}\) và điểm cực viễn \(O{C_V}\). Để sửa tật của mắt người này thì người đó phải đeo sát mắt một kính có tiêu cực là:
-
A.
\(f = O{C_C}\)
-
B.
\(f = - O{C_C}\)
-
C.
\(f = O{C_V}\)
-
D.
\(f = - O{C_V}\)
Một người bị cận thị có khoảng cách từ thể thuỷ tinh đến điểm cực cận là \(O{C_C}\) và điểm cực viễn \(O{C_V}\). Để sửa tật của mắt người này thì người đó phải đeo sát mắt một kính có tiêu cực là:
-
A.
\(f = O{C_C}\)
-
B.
\(f = - O{C_C}\)
-
C.
\(f = O{C_V}\)
-
D.
\(f = - O{C_V}\)
Một người cận thị phải đeo sát mắt kính cận số 0,5. Nếu xem ti vi mà không muốn đeo kính thì người đó phải cách màn hình xa nhất một đoạn
-
A.
0,5m
-
B.
1 m
-
C.
1.5 m
-
D.
2 m
Một người cận thị về già, khi đọc sách cách mắt gần nhất 25cm phải đeo sát mắt kính số 2. Điểm cực cận của người đó nằm trên trục của mắt và cách mắt
-
A.
25 cm
-
B.
50 cm
-
C.
1 m
-
D.
2 m
Một người viễn thị có điểm cực cận cách mắt 50cm. Khi đeo sát mắt một kính có độ tụ +1dp, người này sẽ nhìn rõ được những vật gần nhất cách mắt
-
A.
40 cm
-
B.
33.3 cm
-
C.
27.5 cm
-
D.
26.7 cm
Một người viễn thị có điểm cực cận cách mắt gần nhất 40cm. Để nhìn rõ vật đặt cách mắt gần nhất 25cm, người này cần đeo kính ( đeo sát mắt) có độ tụ là:
-
A.
-2.5dp
-
B.
2.5dp
-
C.
-1.5dp
-
D.
1.5dp
Một người cận thị có khoảng nhìn rõ từ 12,5cm đến 50cm. Khi đeo kính ( đeo sát mắt ) chữa tật của mắt để khi nhìn vật ở vô cực mà mắt không điều tiết, người này nhìn rõ được các vật đặt gần nhất cách mắt
-
A.
15 cm
-
B.
16.7 cm
-
C.
17.5 cm
-
D.
22.5 cm
Một người cận thị có khoảng nhìn rõ từ 12,5cm đến 50cm. Khi đeo kính ( đeo sát mắt) có độ tụ -1dp. Khoảng nhìn rõ của người này khi đeo kính là
-
A.
từ 13,3cm đến 75cm
-
B.
từ 14,3cm đến 75cm
-
C.
từ 14,3cm đến 100cm
-
D.
từ 13,3cm đến 100cm
Một người viễn thị nhìn rõ được vật đặt cách mắt gần nhất 40cm. Để nhìn rõ vật đặt cách mắt gần nhất 25cm, người này cần đeo kính ( kính cách mắt 1cm) có độ tụ là
-
A.
1.4 dp
-
B.
1.5 dp
-
C.
1.6 dp
-
D.
1.7 dp
Mắt một người cận thị có khoảng nhìn rõ từ 12cm đến 51cm. Người đó sửa tật bằng cách đeo kính phân kì cách mắt 1cm. Biết năng suất phân li của mắt là 1’. Khoảng cách nhỏ nhất giữa hai điểm trên vật mà mắt còn có thể phân biệt được là
-
A.
0,033mm
-
B.
0,043mm
-
C.
0,067mm
-
D.
0,044mm
Mắt một người có điểm cực viễn cách mắt 50cm và độ biến thiên độ tụ từ trạng thái mắt không điều tiết đến trạng thái mắt điều tiết tối đa là 8dp. Hỏi điểm cực cận của mắt người này cách mắt bao nhiêu?
-
A.
8 cm
-
B.
5 cm
-
C.
10 cm
-
D.
3 cm
Trên một tờ giấy vẽ hai vạch cách nhau 1mm. Đưa tờ giấy xa mắt dần cho đến khi thấy hai vạch đó gần như nằm trên một đường thẳng. Xác định gần đúng khoảng cách từ mắt đến tờ giấy. Biết năng suất phân li của mắt người này là \({\alpha _{\min }} = {3.10^{ - 4}}ra{\rm{d}}\).
-
A.
3,33m
-
B.
3,33cm
-
C.
4,5m
-
D.
4,5cm
Một mắt bình thường có võng mạc cách thủy tinh thể một đoạn 15mm. Hãy xác định độ tụ của thủy tinh thể khi nhìn vật AB trong các trường hợp
Vật AB ở vô cực?
-
A.
66,67dp
-
B.
33,4dp
-
C.
15dp
-
D.
78,8dp
Vật AB cách mắt 80cm?
-
A.
66,67dp
-
B.
67,92dp
-
C.
63,72dp
-
D.
66,56dp
Một vật AB đặt cách mắt 5m. Hãy xác định độ cao tối thiểu của vật AB để mắt phân biệt được hai điểm A, B. Biết năng suất phân li của mắt \({\alpha _{\min }} = {3.10^{ - 4}}\left( {ra{\rm{d}}} \right)\)
-
A.
2 mm
-
B.
1 mm
-
C.
1,5 mm
-
D.
2,5 mm
Mắt một người có điểm cực viễn cách mắt 50cm
Mắt người này bị tật gì?
-
A.
Cận thị
-
B.
Viễn thị
-
C.
Lão thị
-
D.
Bình thường
Muốn nhìn thấy vật ở vô cực không phải điều tiết, người đó phải đeo kính có độ tụ bao nhiêu (coi kính đeo sát mắt)?
-
A.
2dp
-
B.
-2dp
-
C.
0,5dp
-
D.
-0,5dp
Điểm \({C_C}\) cách mắt \(10cm\), khi đeo kính trên (sát mắt) thì người đó nhìn thấy điểm gần nhất cách mắt bao nhiêu?
-
A.
12,5cm
-
B.
50cm
-
C.
15cm
-
D.
10cm
Một người đeo kính sát mắt một kính có độ tụ \(D = - 1,25{\rm{d}}p\) nhìn rõ những vật nằm trong khoảng từ 20cm đến rất xa. Người này mắc tật gì?
-
A.
Cận thị
-
B.
Viễn thị
-
C.
Lão thị
-
D.
Không mắc tật gì
Một người cận thị có giới hạn nhìn rõ từ 20cm đến 50cm. Có thể sửa tật cận thị của người đó bằng hai cách:
- Đeo kính cận \({L_1}\) để có thể nhìn rõ vật ở rất xa
- Đeo kính cận \({L_2}\) để có thể nhìn vật ở gần nhất 25cm
Số kính của \({L_1};{L_2}\)là:
-
A.
\( - 2\) và \( - 1\)
-
B.
\( - 1\) và \( - 2\)
-
C.
\(2\)
-
D.
\(1\)
Tìm khoảng cách cực cận khi đeo kính \({L_1}\) và khoảng cực viễn khi đeo kính \({L_2}\)?
-
A.
20cm và 50cm
-
B.
20cm và 100cm
-
C.
33,3cm và 100cm
-
D.
50cm và 100cm
Ta nên sửa tật cận thị theo cách nào thì có lợi hơn? vì sao?
-
A.
Đeo kính \({L_1}\) có lợi hơn vì kính \({L_1}\) có phạm vi nhìn lớn hơn
-
B.
Đeo kính \({L_1}\) có lợi hơn vì kính \({L_2}\) có phạm vi nhìn lớn hơn
-
C.
Đeo kính \({L_2}\) có lợi hơn vì kính \({L_2}\) có phạm vi nhìn lớn hơn
-
D.
Cả hai cách như nhau.
Một thấu kính hội tụ \({L_1}\) tạo ảnh thật cao bằng nửa vật khi vật đặt cách thấu kính 15cm
Tiêu cự của thấu kính là:
-
A.
10 cm
-
B.
7,5 cm
-
C.
5 cm
-
D.
15 cm
Đặt kính \({L_1}\) cách mắt một người \(5cm\) rồi di chuyển một vật trước kính thì thấy rằng mắt nhìn rõ vật cách mắt 75mm đến 95mm. Xác định khoảng cực cận và khoảng cực viễn của mắt?
-
A.
\(O{C_C} = 5cm;O{C_V} = 55cm\)
-
B.
\(O{C_C} = 20cm;O{C_V} = 170cm\)
-
C.
\(O{C_C} = 10cm;O{C_V} = 50cm\)
-
D.
\(O{C_C} = 75mm;O{C_V} = 95mm\)
Mắt của một người có thể nhìn rõ những vật đặt cách mắt trong khoảng từ 50 cm đến vô cực. Người này dùng kính lúp có độ tụ D = +20 dp để quan sát các vật nhỏ. Mặt đặt sát kính. Để quan sát rõ nét ảnh của vật qua kính lúp thì vật phải đặt cách kính một đoạn d thỏa mãn điều kiện nào sau đây?
-
A.
\(4,45cm \le d \le 4,72cm\)
-
B.
\(4,55cm \le d \le 5cm\)
-
C.
\(5cm \le d \le 6,25cm\)
-
D.
\(4,72cm \le d \le 6cm\)
Một người cận thị có khoảng nhìn rõ từ 12 cm đến 44 cm. Khi đeo kính sát mắt để sửa tật thì nhìn được vật gần nhất cách mắt là
-
A.
9,5 cm.
-
B.
16,5 cm.
-
C.
18,5 cm.
-
D.
20,0 cm.
Một học sinh nhìn thấy rõ những vật ở cách mắt từ 11cm đến 101 cm. Học sinh đó đeo kính cận đặt cách mắt 1 cm để nhìn rõ các vật ở vô cực mà không phải điều tiết. Khi đeo kính này, vật gần nhất mà học sinh đó nhìn rõ cách mắt một khoảng là
-
A.
11,11 cm.
-
B.
16,7 cm.
-
C.
14,3 cm.
-
D.
12,11 cm.
Một người mắt không có tật, có điểm cực cận cách mặt x (m). Khi điều tiết tối đa thì độ tụ của mất tăng thêm 1 dp so với khi không điều tiết. Độ tụ của thấu kính phải đeo để nhìn thấy một vật cách mắt 25 cm trong trạng thái điều tiết tối đa là D. Giá trị của D gần nhất với giá trị nào sau đây? Biết rằng kính đeo cách mắt 2 cm.
-
A.
2
-
B.
4,2
-
C.
3,3
-
D.
1,9
Một người cận thị có điểm cực viễn cách mắt 100cm. Tính độ tụ của kính phải đeo sát mắt để mắt có thể nhìn vật ở vô cực không phải điều tiết
-
A.
1dp
-
B.
– 2dp
-
C.
– 1dp
-
D.
2dp
Một người cận thị phải đeo sát mắt một kính có độ tụ - 4dp, nhìn rõ được các vật ở vô cực. Điểm cực viễn của mắt người ấy khi không đeo kính cách mắt một khoảng là
-
A.
OCV = 40cm
-
B.
OCV = 4cm
-
C.
OCV = 25cm
-
D.
OCV = 400cm
Một người viễn thị có điểm cực cận cách mắt 40cm. Để có thể nhìn thấy vật gần nhất cách mắt 25cm, người đó cần đeo sát mắt một kính có độ tụ bằng
-
A.
1,5 điôp.
-
B.
- 1,5 điôp.
-
C.
- 1,25 điôp.
-
D.
1,25 điôp.
Lời giải và đáp án
Một người bị cận thị có khoảng cách từ thể thuỷ tinh đến điểm cực cận là \(O{C_C}\) và điểm cực viễn \(O{C_V}\). Để sửa tật của mắt người này thì người đó phải đeo sát mắt một kính có tiêu cực là:
-
A.
\(f = O{C_C}\)
-
B.
\(f = - O{C_C}\)
-
C.
\(f = O{C_V}\)
-
D.
\(f = - O{C_V}\)
Đáp án : D
Sử dụng lí thuyết cách khắc phục tật của mắt
Để sửa tật của mắt người bị cận thì người đó phải đeo sát mắt một kính có tiêu cự là: \(f = - O{C_V}\)
Một người bị cận thị có khoảng cách từ thể thuỷ tinh đến điểm cực cận là \(O{C_C}\) và điểm cực viễn \(O{C_V}\). Để sửa tật của mắt người này thì người đó phải đeo sát mắt một kính có tiêu cực là:
-
A.
\(f = O{C_C}\)
-
B.
\(f = - O{C_C}\)
-
C.
\(f = O{C_V}\)
-
D.
\(f = - O{C_V}\)
Đáp án : D
Sử dụng lí thuyết cách khắc phục tật của mắt
Để sửa tật của mắt người bị cận thì người đó phải đeo sát mắt một kính có tiêu cự là: \(f = - O{C_V}\)
Một người cận thị phải đeo sát mắt kính cận số 0,5. Nếu xem ti vi mà không muốn đeo kính thì người đó phải cách màn hình xa nhất một đoạn
-
A.
0,5m
-
B.
1 m
-
C.
1.5 m
-
D.
2 m
Đáp án : D
+ Áp dụng biểu thức xác định tiêu cự của thấu kính: \(f = \frac{1}{D}\)
+ Để sửa tật của mắt người bị cận thì người đó phải đeo sát mắt một kính có tiêu cự là: \(f = - O{C_V}\)
Ta có:
+ Kính cận số 0,5 có \(D = - 0,5dp \to f = - 2m\)
+ Mặt khác: \(f = - O{C_V} \to O{C_V} = 2m\)
Nếu xem ti vi mà không muốn đeo kính thì người đó phải cách màn hình xa nhất một đoạn 2m
Một người cận thị về già, khi đọc sách cách mắt gần nhất 25cm phải đeo sát mắt kính số 2. Điểm cực cận của người đó nằm trên trục của mắt và cách mắt
-
A.
25 cm
-
B.
50 cm
-
C.
1 m
-
D.
2 m
Đáp án : B
+ Áp dụng biểu thức xác định tiêu cự của thấu kính: \(f = \frac{1}{D}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Kính cận số 2 có \(D = - 2dp \to f = - 0,5m\)
+ Quan sát vật cách mắt 25cm qua kính => OCc= -d’=-df/(d+f)=50cm
Một người viễn thị có điểm cực cận cách mắt 50cm. Khi đeo sát mắt một kính có độ tụ +1dp, người này sẽ nhìn rõ được những vật gần nhất cách mắt
-
A.
40 cm
-
B.
33.3 cm
-
C.
27.5 cm
-
D.
26.7 cm
Đáp án : B
+ Áp dụng biểu thức xác định tiêu cự của thấu kính: \(f = \frac{1}{D}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Ta có: \(D = 1dp \to f = 1m\)
+ Quan sát vật cách mắt 50cm qua kính:
\( \to O{C_C} = - d' \to d = \frac{{d'f}}{{d' - f}} = 33.3cm\)
Một người viễn thị có điểm cực cận cách mắt gần nhất 40cm. Để nhìn rõ vật đặt cách mắt gần nhất 25cm, người này cần đeo kính ( đeo sát mắt) có độ tụ là:
-
A.
-2.5dp
-
B.
2.5dp
-
C.
-1.5dp
-
D.
1.5dp
Đáp án : D
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Áp dụng biểu thức xác định tiêu cự của thấu kính: \(f = \frac{1}{D}\)
+ Theo công thức thấu kính: \(D = \frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{0,25}} + \frac{1}{{ - 0,4}} = 1,5dp\)
Một người cận thị có khoảng nhìn rõ từ 12,5cm đến 50cm. Khi đeo kính ( đeo sát mắt ) chữa tật của mắt để khi nhìn vật ở vô cực mà mắt không điều tiết, người này nhìn rõ được các vật đặt gần nhất cách mắt
-
A.
15 cm
-
B.
16.7 cm
-
C.
17.5 cm
-
D.
22.5 cm
Đáp án : B
+ Để sửa tật cận thị, đeo kính có \(f = - O{C_V}\)
+ Quan sát ở cực cận: \(d' = - O{C_C}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Người đó sửa tật khi đeo kính có f= -OCv= -50cm
+ Quan sát ở cực cận: d’= -OCc= -12.5cm => d=d'f/(d'-f)=16,7cm
Một người cận thị có khoảng nhìn rõ từ 12,5cm đến 50cm. Khi đeo kính ( đeo sát mắt) có độ tụ -1dp. Khoảng nhìn rõ của người này khi đeo kính là
-
A.
từ 13,3cm đến 75cm
-
B.
từ 14,3cm đến 75cm
-
C.
từ 14,3cm đến 100cm
-
D.
từ 13,3cm đến 100cm
Đáp án : C
Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Người đó đeo kính có f= -1m
=> Quan sát ở cực cận: \(d' = - O{C_C} = - 12,5cm \to {d_C} = \frac{{d'f}}{{d' - f}} = 14,3cm\)
=> Quan sát ở cực viễn : \(d' = - O{C_v} = - 50cm \to {d_V} = \frac{{d'f}}{{d' - f}} = 100cm\)
=> Khoảng nhìn rõ của người này khi đeo kính là \(14,3cm - 100cm\)
Một người viễn thị nhìn rõ được vật đặt cách mắt gần nhất 40cm. Để nhìn rõ vật đặt cách mắt gần nhất 25cm, người này cần đeo kính ( kính cách mắt 1cm) có độ tụ là
-
A.
1.4 dp
-
B.
1.5 dp
-
C.
1.6 dp
-
D.
1.7 dp
Đáp án : C
+ Người đó sửa tật khi đeo kính có: \(d' = - OC_{C} + l\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Người đó sửa tật khi đeo kính có:\(d' = - OC_{C} + l = - 39cm\)
+ Quan sát ở cực cận: \(d = 25 - 1 = 24cm\)
\(D = \frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{0,24}} + \frac{1}{{ - 0,39}} = 1,6dp\)
Mắt một người cận thị có khoảng nhìn rõ từ 12cm đến 51cm. Người đó sửa tật bằng cách đeo kính phân kì cách mắt 1cm. Biết năng suất phân li của mắt là 1’. Khoảng cách nhỏ nhất giữa hai điểm trên vật mà mắt còn có thể phân biệt được là
-
A.
0,033mm
-
B.
0,043mm
-
C.
0,067mm
-
D.
0,044mm
Đáp án : D
+ Người đó sửa tật khi đeo kính có: \(d' = - O{C_C} + l\)
+ Sử dụng công thức thấu kính: \(k = \dfrac{{A'B'}}{{AB}} = \dfrac{{ - d' - f}}{f}\)
+ Người đó sửa tật khi đeo kính có \(f = - O{C_C} + l = - 50cm\)
+ Khoảng cách nhỏ nhất giữa hai điểm trên vật khi quan át ở cực cận có ảnh cách mắt \(l = 12cm\)
=> Khoảng cách nhỏ nhất hai điểm trên ảnh là:\(A'B' = l\alpha \)
Trong đó: \(\alpha = 1' = \dfrac{1}{{60}}\) độ = \(\dfrac{1}{{60}}.\dfrac{\pi }{{180}}\) (rad)
Suy ra: \(A'B' = l\alpha = 12.\dfrac{1}{{60}}\dfrac{\pi }{{180}} = 3,{49.10^{ - 3}}cm = 0,0349mm\)
+ Ảnh nằm cách kính một đoạn \(d' = - 11cm\)
Theo công thức thấu kính:
\(\begin{array}{l}k = \dfrac{{A'B'}}{{AB}} = \dfrac{{ - d' - f}}{f} = \dfrac{{ - \left( { - 11 + 50} \right)}}{{ - 50}} = 0,78\\ \to AB = \dfrac{{A'B'}}{{0,78}} = \dfrac{{0,0349}}{{0,78}} = 0,0447mm\end{array}\)
Mắt một người có điểm cực viễn cách mắt 50cm và độ biến thiên độ tụ từ trạng thái mắt không điều tiết đến trạng thái mắt điều tiết tối đa là 8dp. Hỏi điểm cực cận của mắt người này cách mắt bao nhiêu?
-
A.
8 cm
-
B.
5 cm
-
C.
10 cm
-
D.
3 cm
Đáp án : C
Vận dụng công thức biến thiên độ tụ khi chuyển từ trạng thái không điều tiết sang điều tiết tối đa: \(\Delta D = \frac{1}{{O{C_C}}} - \frac{1}{{O{C_V}}}\)
Ta có: biến thiên độ tụ khi chuyển từ trạng thái khống điều tiết sang điều tiết tối đa: \(\begin{array}{l}\Delta D = \frac{1}{{O{C_C}}} - \frac{1}{{O{C_V}}} \leftrightarrow 8 = \frac{1}{{O{C_C}}} - \frac{1}{{0,5}}\\ \to O{C_C} = 0,1m = 10cm\end{array}\)
Trên một tờ giấy vẽ hai vạch cách nhau 1mm. Đưa tờ giấy xa mắt dần cho đến khi thấy hai vạch đó gần như nằm trên một đường thẳng. Xác định gần đúng khoảng cách từ mắt đến tờ giấy. Biết năng suất phân li của mắt người này là \({\alpha _{\min }} = {3.10^{ - 4}}ra{\rm{d}}\).
-
A.
3,33m
-
B.
3,33cm
-
C.
4,5m
-
D.
4,5cm
Đáp án : A
+ Vận dụng biểu thức tính góc trông của mắt: \(\tan \alpha = \frac{{AB}}{l}\)
+Sử dụng công thức gần đúng: \(\alpha \ll \to \tan \alpha \approx \alpha \)
Ta có:
+ Khoảng cách giữa hai vạch xem như vật AB có chiều cao 1mm
+ Góc trông vật của mắt: \(\tan \alpha = \frac{{AB}}{l}\) (với \(l\) là khoảng cách từ mắt đến tờ giấy)
+ Khi mắt thấy hai vạch đó như nằm trên một đường thẳng thì \({\alpha _{\min }}\), khi đó
\(\begin{array}{l}\tan {a_{\min }} = \frac{{AB}}{{{l_{{\rm{max}}}}}}\\ \to {l_{{\rm{max}}}} = \frac{{AB}}{{\tan {\alpha _{\min }}}} \approx \frac{{AB}}{{{\alpha _{\min }}}} = \frac{{{{10}^{ - 3}}}}{{{{3.10}^{ - 4}}}} = 3,33m\end{array}\)
Một mắt bình thường có võng mạc cách thủy tinh thể một đoạn 15mm. Hãy xác định độ tụ của thủy tinh thể khi nhìn vật AB trong các trường hợp
Vật AB ở vô cực?
-
A.
66,67dp
-
B.
33,4dp
-
C.
15dp
-
D.
78,8dp
Đáp án: A
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Áp dụng công thức tính độ tụ: \(D = \frac{1}{f}\)
Ta có, mắt bình thường cho ảnh trên võng mạc nên \( \to d' = OV = 15mm\)
+ Khi nhìn vật ở vô cực \(\left( {d = \infty } \right)\), ảnh hiện trên võng mạc.
+ Tiêu cự của thủy tinh thế là:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{OV}}\\ \to f = OV = 15mm\end{array}\)
+ Độ tụ của thủy tinh thể: \(D = \frac{1}{f} = \frac{1}{{{{15.10}^{ - 3}}}} = 66,67{\rm{d}}p\)
Vật AB cách mắt 80cm?
-
A.
66,67dp
-
B.
67,92dp
-
C.
63,72dp
-
D.
66,56dp
Đáp án: B
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Áp dụng công thức tính độ tụ: \(D = \frac{1}{f}\)
Ta có, mắt bình thường cho ảnh trên võng mạc nên \( \to d' = OV = 15mm\)
+ \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{80}} + \frac{1}{{1,5}} = 1,47cm\)
+ Độ tụ của thủy tinh thể: \(D = \frac{1}{f} = \frac{1}{{0,0147}} = 67,92{\rm{d}}p\)
Một vật AB đặt cách mắt 5m. Hãy xác định độ cao tối thiểu của vật AB để mắt phân biệt được hai điểm A, B. Biết năng suất phân li của mắt \({\alpha _{\min }} = {3.10^{ - 4}}\left( {ra{\rm{d}}} \right)\)
-
A.
2 mm
-
B.
1 mm
-
C.
1,5 mm
-
D.
2,5 mm
Đáp án : C
+ Sử dụng công thức tính góc trông vật của mắt: \(\tan \alpha = \frac{{AB}}{l}\)
+ Sử dụng công thức gần đúng: \(\tan \alpha \approx \alpha \) khi \(\alpha \ll \)
+ Áp dụng điều kiện để mắt phân biệt được 2 điểm A, B là: \(\alpha \ge {\alpha _{\min }}\)
Ta có:
+ Góc trông vật của mắt: \(\tan \alpha = \frac{{AB}}{l}\) (với \(l\) là khoảng cách từ mắt đến vật AB)
+ Vì góc trông nhỏ, nên ta có: \(\tan \alpha \approx \alpha = \frac{{AB}}{l}\)
+ Điều kiện để mắt phân biệt được 2 điểm A, B là: \(\alpha \ge {\alpha _{\min }}\)
\( \to \frac{{AB}}{l} \ge {\alpha _{\min }} \to AB \ge l.{\alpha _{\min }} = {5.3.10^{ - 4}} = 1,{5.10^{ - 3}}m = 1,5mm\)
Vậy chiều cao tối thiểu của vật là \(1,5mm\)
Mắt một người có điểm cực viễn cách mắt 50cm
Mắt người này bị tật gì?
-
A.
Cận thị
-
B.
Viễn thị
-
C.
Lão thị
-
D.
Bình thường
Đáp án: A
: Sử dụng lí thuyết về các tật của mắt
Ta thấy, mắt người này nhìn xa nhất là 50cm nên mắt người này bị cận thị
Muốn nhìn thấy vật ở vô cực không phải điều tiết, người đó phải đeo kính có độ tụ bao nhiêu (coi kính đeo sát mắt)?
-
A.
2dp
-
B.
-2dp
-
C.
0,5dp
-
D.
-0,5dp
Đáp án: B
+ Mắt không phải điều tiết khi nhìn ở vô cực
+ Sử dụng công thức: \(D = \frac{1}{\infty } + \frac{1}{{ - O{C_V}}}\)
+ Khi mắt nhìn ở vô cực thì không phải điều tiết.
=> Người này phải đeo kính có độ tụ \({D_1}\) sao cho vật đặt ở vô cực cho ảnh ảo ở điểm cực viễn của mắt.
Do đó, ta có: \(D = \frac{1}{\infty } + \frac{1}{{ - O{C_V}}} = - \frac{1}{{0,5}} \to D = - 2{\rm{d}}p\)
Điểm \({C_C}\) cách mắt \(10cm\), khi đeo kính trên (sát mắt) thì người đó nhìn thấy điểm gần nhất cách mắt bao nhiêu?
-
A.
12,5cm
-
B.
50cm
-
C.
15cm
-
D.
10cm
Đáp án: A
Sử dụng công thức thấu kính: \(D = \frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Khi đeo kính trên mà nhìn vật cách mắt đoạn gần nhất là d thì ảnh ảo sẽ hiện ở điểm cực cận của mắt \(\left( {d' = - 10cm} \right)\)
Ta có:
\(\begin{array}{l}D = \frac{1}{d} + \frac{1}{{d'}} \leftrightarrow - 2 = \frac{1}{d} + \frac{1}{{ - 0,1}}\\ \to d = 0,125m = 12,5cm\end{array}\)
Một người đeo kính sát mắt một kính có độ tụ \(D = - 1,25{\rm{d}}p\) nhìn rõ những vật nằm trong khoảng từ 20cm đến rất xa. Người này mắc tật gì?
-
A.
Cận thị
-
B.
Viễn thị
-
C.
Lão thị
-
D.
Không mắc tật gì
Đáp án : A
+ Sử dụng công thức tính tiêu cự của thấu kính: \(f = \frac{1}{D}\)
+ Sử dụng lí thuyết về các tật của mắt
Ta có:
+ Tiêu cự của thấu kính: \(f = \frac{1}{D} = - 0,8m = - 80cm\)
+ Vật ở rất xa tức là \(d = \infty \), cho ảnh \(d' = f = - 80cm\) là ảnh ảo tước thấu kính (tức là trước mắt) là 80cm
=> Vậy điểm cực viễn cách mắt \(80cm < \infty \) nên mắt đó là mắt cận thị.
Một người cận thị có giới hạn nhìn rõ từ 20cm đến 50cm. Có thể sửa tật cận thị của người đó bằng hai cách:
- Đeo kính cận \({L_1}\) để có thể nhìn rõ vật ở rất xa
- Đeo kính cận \({L_2}\) để có thể nhìn vật ở gần nhất 25cm
Số kính của \({L_1};{L_2}\)là:
-
A.
\( - 2\) và \( - 1\)
-
B.
\( - 1\) và \( - 2\)
-
C.
\(2\)
-
D.
\(1\)
Đáp án: A
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Sử dụng công thức tính độ tụ: \(D = \frac{1}{f}\)
+ Số kính chính là độ tụ của kính
- Khi đeo kính \({L_1}\):
+ Qua \({L_1}\) vật ở vô cực cho ảnh ảo ở điểm cực viễn của mắt cận.
Ta có: \(\left\{ \begin{array}{l}d = \infty \\d' = - 50cm\end{array} \right. \to \frac{1}{{{f_1}}} = \frac{1}{\infty } + \frac{1}{{ - 50}} \to {f_1} = - 50cm = - 0,5m\)
+ Độ tụ: \({D_1} = \frac{1}{{{f_1}}} = - 2{\rm{d}}p\)
- Khi đeo kính \({L_2}\) :
+ Vật ở cách mắt 25cm cho ảnh ảo ở điểm cực cận của mắt.
Ta có: \(\left\{ \begin{array}{l}d = 25cm\\d' = - 20cm\end{array} \right. \to \frac{1}{{{f_2}}} = \frac{1}{{25}} + \frac{1}{{ - 20}} \to {f_2} = - 100cm = - 1m\)
+ Độ tụ: \(D = \frac{1}{f} = - 1{\rm{d}}p\)
Tìm khoảng cách cực cận khi đeo kính \({L_1}\) và khoảng cực viễn khi đeo kính \({L_2}\)?
-
A.
20cm và 50cm
-
B.
20cm và 100cm
-
C.
33,3cm và 100cm
-
D.
50cm và 100cm
Đáp án: C
+ Sử dụng lí thuyết về sự tạo ảnh của vật qua thấu kính
+ Áp dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
- Khoảng cực cận khi đeo kính \({L_1}\)
+ Vật chỉ có thể đặt gần mắt nhất ở vị trí cho ảnh ảo ở điểm cực cận của mắt.
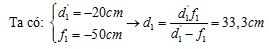
Vậy điểm gần nhất khi đeo kính \({L_1}\) còn nhìn rõ vật cách mắt là 33,3cm
- Khoảng cực cận khi đeo kính \({L_2}\)
+ Vật chỉ có thể đặt xa mắt nhất ở vị trí cho ảnh ảo ở điểm cực viễn của mắt:
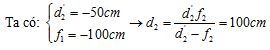
Vậy điểm xa nhất khi đeo kính \({L_2}\) còn nhìn rõ vật cách mắt là 100cm
Ta nên sửa tật cận thị theo cách nào thì có lợi hơn? vì sao?
-
A.
Đeo kính \({L_1}\) có lợi hơn vì kính \({L_1}\) có phạm vi nhìn lớn hơn
-
B.
Đeo kính \({L_1}\) có lợi hơn vì kính \({L_2}\) có phạm vi nhìn lớn hơn
-
C.
Đeo kính \({L_2}\) có lợi hơn vì kính \({L_2}\) có phạm vi nhìn lớn hơn
-
D.
Cả hai cách như nhau.
Đáp án: A
Vận dụng khoảng nhìn rõ vật
Ta nhận thấy,
+ Khi đeo kính \({L_1}\) phạm vi nhìn từ \(33,3cm\) đến vô cùng
+ Khi đeo kính \({L_2}\) phạm vi nhìn từ \(25cm\) đến \(100cm\)
=> Đeo kính \({L_1}\) lợi hơn vì nó có khoảng nhìn rõ rộng hơn
Một thấu kính hội tụ \({L_1}\) tạo ảnh thật cao bằng nửa vật khi vật đặt cách thấu kính 15cm
Tiêu cự của thấu kính là:
-
A.
10 cm
-
B.
7,5 cm
-
C.
5 cm
-
D.
15 cm
Đáp án: C
+ Sử dụng công thức xác định hệ số phóng đại: \(k = - \frac{{d'}}{d}\)
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
+ Vì vật thật cho ảnh thật nên \(k < 0 \leftrightarrow - \frac{1}{2} = - \frac{{d'}}{d} \to d' = \frac{d}{2} = 7,5cm\)
+ Tiêu cự của thấu kính \(\left( {{L_1}} \right)\): \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to f = \frac{{{\rm{dd}}'}}{{d + d'}} = \frac{{15.7,5}}{{15 + 7,5}} = 5cm\)
Đặt kính \({L_1}\) cách mắt một người \(5cm\) rồi di chuyển một vật trước kính thì thấy rằng mắt nhìn rõ vật cách mắt 75mm đến 95mm. Xác định khoảng cực cận và khoảng cực viễn của mắt?
-
A.
\(O{C_C} = 5cm;O{C_V} = 55cm\)
-
B.
\(O{C_C} = 20cm;O{C_V} = 170cm\)
-
C.
\(O{C_C} = 10cm;O{C_V} = 50cm\)
-
D.
\(O{C_C} = 75mm;O{C_V} = 95mm\)
Đáp án: C
Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Ta có:
+ Khi vật cách mắt \(75mm = 7,5cm\) thì cách kính \({d_1} = 7,5 - 5 = 2,5cm\)
+ Khi vật ở gần thì qua kính cho ảnh ảo ở điểm cực cận của mắt, nên ta có:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{ - \left( {O{C_C} - 5} \right)}}\\ \leftrightarrow \frac{1}{5} = \frac{1}{{2,5}} - \frac{1}{{\left( {O{C_C} - 5} \right)}}\\ \to O{C_C} = 10cm\end{array}\)
+ Khi vật ở xa thì qua kính cho ảnh ảo ở điểm cực viễn của mắt, nên ta có:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{ - \left( {O{C_V} - 5} \right)}}\\ \leftrightarrow \frac{1}{5} = \frac{1}{{4,5}} - \frac{1}{{\left( {O{C_V} - 5} \right)}}\\ \to O{C_V} = 50cm\end{array}\)
Mắt của một người có thể nhìn rõ những vật đặt cách mắt trong khoảng từ 50 cm đến vô cực. Người này dùng kính lúp có độ tụ D = +20 dp để quan sát các vật nhỏ. Mặt đặt sát kính. Để quan sát rõ nét ảnh của vật qua kính lúp thì vật phải đặt cách kính một đoạn d thỏa mãn điều kiện nào sau đây?
-
A.
\(4,45cm \le d \le 4,72cm\)
-
B.
\(4,55cm \le d \le 5cm\)
-
C.
\(5cm \le d \le 6,25cm\)
-
D.
\(4,72cm \le d \le 6cm\)
Đáp án : B
Áp dụng công thức thấu kính \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\)
Khi đặt vật trước kính lúp, để nhìn rõ nét ảnh thì ảnh này hiện ra trong khoảng nhìn rõ của mắt, tức là khi vật gần kính nhất cho ảnh rảo ở CC ; vật xa kính nhất cho ảnh ảo ở CV.
Vật ở gần kính nhất cho ảnh ảo ở CC, ta có:
\(\frac{1}{{{d_1}}} + \frac{1}{{ - O{C_C}}} = \frac{1}{f} \Leftrightarrow \frac{1}{{{d_1}}} + \frac{1}{{ - 0,5}} = 20 \Rightarrow {d_1} = \frac{1}{{22}}m = 4,45cm\)
Vật xa kính nhất cho ảnh ảo ở CV, ta có:
\(\frac{1}{{{d_2}}} + \frac{1}{{ - O{C_v}}} = \frac{1}{f} \Leftrightarrow \frac{1}{{{d_2}}} + \frac{1}{{ - \infty }} = 20 \Rightarrow {d_2} = \frac{1}{{20}}m = 5cm\)
Vật vậy nằm trong khoảng từ 4,45cm đến 5cm
\( \Rightarrow 4,45cm \le d \le 5cm\)
Một người cận thị có khoảng nhìn rõ từ 12 cm đến 44 cm. Khi đeo kính sát mắt để sửa tật thì nhìn được vật gần nhất cách mắt là
-
A.
9,5 cm.
-
B.
16,5 cm.
-
C.
18,5 cm.
-
D.
20,0 cm.
Đáp án : B
Tiêu cự của kính cận: \({f_k} = - O{C_V}\)
Để nhìn được vật gần mắt nhất, ảnh của vật phải nằm ở điểm cực cận
Công thức thấu kính: \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f}\)
Tiêu cự của thấu kính là: \({f_k} = - O{C_V} = - 44\,\,\left( {cm} \right)\)
Để nhìn được vật gần mắt nhất, ảnh của vật phải nằm ở điểm cực cận: \({d_c}' = - O{C_C} = - 12\,\,\left( {cm} \right)\)
Ta có công thức thấu kính:
\(\dfrac{1}{{{d_c}}} + \dfrac{1}{{{d_c}'}} = \dfrac{1}{f} \Rightarrow \dfrac{1}{{{d_c}}} + \dfrac{1}{{ - 12}} = \dfrac{1}{{ - 44}} \Rightarrow {d_c} = 16,5\,\,\left( {cm} \right)\)
Một học sinh nhìn thấy rõ những vật ở cách mắt từ 11cm đến 101 cm. Học sinh đó đeo kính cận đặt cách mắt 1 cm để nhìn rõ các vật ở vô cực mà không phải điều tiết. Khi đeo kính này, vật gần nhất mà học sinh đó nhìn rõ cách mắt một khoảng là
-
A.
11,11 cm.
-
B.
16,7 cm.
-
C.
14,3 cm.
-
D.
12,11 cm.
Đáp án : D
Công thức thấu kính: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)
+ Khi đeo kính cách mắt 1cm, học sinh nhìn rõ các vật ở vô cực mà không phải điều tiết, nên ảnh của vật nằm ở điểm cực viễn của mắt, đồng thời ảnh nằm ở tiêu diện của kính, vậy tiêu cự của kính:
\(f=-\left( 101-1 \right)=-100cm\)
+ Quan sát vật ở gần nhất khi đeo kính, ảnh của vật nằm ở cực cận của mắt, nên cách kính \(\left( 11-1 \right)cm\),
Ta có \({{d}_{C}}'=-10cm\Rightarrow {{d}_{C}}=\frac{{{d}_{C}}'.f}{{{d}_{C}}'-f}=\frac{-10.-100}{-10+100}=11,11cm\)
Vậy vật gần nhất học sinh đó nhìn rõ cách mắt: \(11,11+1=12,11cm\)
Một người mắt không có tật, có điểm cực cận cách mặt x (m). Khi điều tiết tối đa thì độ tụ của mất tăng thêm 1 dp so với khi không điều tiết. Độ tụ của thấu kính phải đeo để nhìn thấy một vật cách mắt 25 cm trong trạng thái điều tiết tối đa là D. Giá trị của D gần nhất với giá trị nào sau đây? Biết rằng kính đeo cách mắt 2 cm.
-
A.
2
-
B.
4,2
-
C.
3,3
-
D.
1,9
Đáp án : C
Mắt người không có tật thì cực viễn ở vô cùng.
Áp dụng công thức độ tụ của mắt khi nhìn vật ở cực cận (điều tiết tối đa) và cực viễn (không điều tiết)
\(\frac{1}{{O{C_c}}} + \frac{1}{{OV}} = \frac{1}{{{f_1}}};\frac{1}{{O{C_v}}} + \frac{1}{{OV}} = \frac{1}{{{f_2}}}\)
Khi đeo kính, sơ đồ tạo ảnh là:
\(\begin{array}{l}
ABA'B'A''B''\\
{d_1}' + {d_2} = O{O_M}
\end{array}\)
Vật ở cách mắt 1 khoảng d = 25cm, ảnh ảo tạo ra ở vị trí cực cận.
Độ tụ của kính là: \(D = \frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{{d_1}'}}\)
Mắt người không có tật thì cực viễn ở vô cùng.
Áp dụng công thức độ tụ của mắt khi nhìn vật ở cực cận (điều tiết tối đa) và cực viễn (không điều tiết)
\(\begin{array}{l}
\left\{ \begin{array}{l}
\frac{1}{{O{C_c}}} + \frac{1}{{OV}} = \frac{1}{{{f_1}}}\\
\frac{1}{{O{C_v}}} + \frac{1}{{OV}} = \frac{1}{{{f_2}}} \Leftrightarrow \frac{1}{\infty } + \frac{1}{{OV}} = \frac{1}{{{f_2}}}
\end{array} \right.\\
{D_{\max }} - {D_{\min }} = 1 \Leftrightarrow \frac{1}{{{f_1}}} - \frac{1}{{{f_2}}} = 1 \Leftrightarrow \frac{1}{{O{C_c}}} = 1 \Rightarrow O{C_C} = 1m
\end{array}\)
Khi đeo kính, sơ đồ tạo ảnh là:
\(\begin{array}{l}
ABA'B'A''B''\\
{d_1}' + {d_2} = O{O_M} \Rightarrow {d_1}' = O{O_M} - {d_2}
\end{array}\)
Vật ở cách kính 1 khoảng \({d_1} = 25 - 2 = 23cm\), ảnh ảo tạo ra ở vị trí cực cận.
Nên \({d_1}' = 2 - O{C_c} = - 98cm\)
Độ tụ của kính là :
\(D = \frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{{d_1}'}} = \frac{1}{{0,23}} + \frac{1}{{ - 0,98}} = 3,32dp\)
Một người cận thị có điểm cực viễn cách mắt 100cm. Tính độ tụ của kính phải đeo sát mắt để mắt có thể nhìn vật ở vô cực không phải điều tiết
-
A.
1dp
-
B.
– 2dp
-
C.
– 1dp
-
D.
2dp
Đáp án : C
Để mắt không phải điều tiết thì vật ở vô cực cho ảnh ở cực viễn, tức là thấu kính phải có tiêu cự f = - OCV
Độ tụ D = 1/f
Để mắt không phải điều tiết thì vật ở vô cực cho ảnh ở cực viễn, tức là thấu kính phải có tiêu cự f = - OCV = - 100cm = -1m
Độ tụ của kính là: \(D = \frac{1}{f} = - 1dp\)
Một người cận thị phải đeo sát mắt một kính có độ tụ - 4dp, nhìn rõ được các vật ở vô cực. Điểm cực viễn của mắt người ấy khi không đeo kính cách mắt một khoảng là
-
A.
OCV = 40cm
-
B.
OCV = 4cm
-
C.
OCV = 25cm
-
D.
OCV = 400cm
Đáp án : C
Người bị tật cận thị phải đeo kính phân kỳ có tiêu cự bằng khoảng cực viễn
Độ tụ của kính D = 1/f
Tiêu cự kính phân kỳ người đó phải đeo là f = 1/D = - 0,25m
Vậy điểm cực viễn khi không đeo kính cách mắt 0,25m = 25cm
Một người viễn thị có điểm cực cận cách mắt 40cm. Để có thể nhìn thấy vật gần nhất cách mắt 25cm, người đó cần đeo sát mắt một kính có độ tụ bằng
-
A.
1,5 điôp.
-
B.
- 1,5 điôp.
-
C.
- 1,25 điôp.
-
D.
1,25 điôp.
Đáp án : A
Để nhìn được vật gần nhất thì vật đó phải cho ảnh ở điểm cực cận.
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Khi d = 25cm thì d’ = - 40cm \( \Rightarrow \frac{1}{f} = \frac{1}{{0,25}} - \frac{1}{{0,40}} = 1,5dp\)
Luyện tập và củng cố kiến thức Bài 32. Kính lúp Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 33. Kính hiển vi Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 34. Kính thiên văn Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập chương 7 Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 31. Mắt Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 29. Các dạng bài tập thấu kính Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập thấu kính (phần 2) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tông hợp bài tập thấu kính (phần 1) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 28. Lăng kính - Bài tập lăng kính Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
