Trắc nghiệm Bài 34. Kính thiên văn - Vật Lí 11
Đề bài
Người ta dùng kính thiên văn để quan sát những
-
A.
vật rất nhỏ ở gần
-
B.
vật nhỏ ở ngang trước vật kính
-
C.
thiên thể ở xa
-
D.
ngôi nhà cao tầng
Khi nói về cách sử dụng kính thiên văn, phát biểu nào sau đây đúng?
-
A.
Điều chỉnh khoảng cách giữa vật và vật kính sao cho ảnh của vật qua kính nằm trong khoảng nhìn rõ của mắt
-
B.
Điều chỉnh khoảng cách giữa vật kính và thị kính sao cho ảnh của vật qua kính nằm trong khoảng nhìn rõ của mắt
-
C.
Giữ nguyên khoảng cách giữa vật kính và thị kính, thay đổi khoảng cách giữa kính với vật sao cho ảnh của vật qua kính nằm trong khoảng nhìn rõ của mắt
-
D.
Giữ nguyên khoảng cách giữa vật kính và thị kính, thay đổi khoảng cách giữa mắt và thị kính sao cho ảnh của vật qua kính nằm trong khoảng nhìn rõ của mắt
Khi nói về cấu tạo của lăng kính thiên văn, phát biểu nào sau đây là đúng?
-
A.
Vật kính là thấu kính phân kì có tiêu cự rất ngắn, thị kính là thấu kính hội tụ có tiêu cự ngắn
-
B.
Vật kính là thấu kính hội tụ có tiêu cự rất ngắn, thị kính là thấu kính phân kì có tiêu cự ngắn
-
C.
Vật kính là thấu kính hội tụ có tiêu cự dài, thị kính là thấu kính hội tụ có tiêu cự ngắn
-
D.
Vật kính là thấu kính phân kì có tiêu cự dài, thị kính là thấu kính phân kì có tiêu cự ngắn
Người ta điều chỉnh kính thiên văn theo cách nào sau đây?
-
A.
Thay đổi khoảng cách giữa vật kính và thị kính bằng cách giữ nguyên vật kính, dịch chuyển thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất
-
B.
Thay đổi khoảng cách giữa vật kính và thị kính bằng cách dịch chuyển thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất
-
C.
Thay đổi khoảng cách giữa vật kính và thị kính bằng cách giữ nguyên thị kính, dịch chuyển vật kính sao cho nhìn thấy ảnh của vật to và rõ nhất
-
D.
Dịch chuyển thích hợp cả vật kính và thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất
Dùng kính thiên văn gồm vật kính và thị kính là thấu kính hội tụ có tiêu cự tương ứng là \({f_1}\) và \({f_2}\). Một người sử dụng kính này ngắm chừng ở vô cực thì khoảng cách giữa vật kính và thị kính là:
-
A.
\(\frac{{{f_1}{f_2}}}{{{f_1} + {f_2}}}\)
-
B.
\({f_1} - {f_2}\)
-
C.
\(\frac{{{f_1}{f_2}}}{{{f_1} - {f_2}}}\)
-
D.
\({f_1} + {f_2}\)
Dùng kính thiên văn gồm vật kính và thị kính là thấu kính hội tụ có tiêu cự tương ứng là \({f_1}\) và \({f_2}\). Khoảng cách giữa hai tiêu điểm chính gần nhất của hai thấu kính là \(\delta \). Người sử dụng kính có điểm cực cận cách mắt đoạn \(O{C_c} = Đ\). Ảnh của vật qua vật kính có số phóng đại \({k_1}\). Số bội giác của kính này khi ngắm chừng ở vô cực được tính theo công thức:
-
A.
${G_\infty } = \frac{Đ}{{{f_2}}}$
-
B.
\({G_\infty } = {k_1}{G_{2\infty }}\)
-
C.
${G_\infty } = \frac{{\delta }}{{{f_1}{f_2}}}$
-
D.
\({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
Ý kiến nào sau đây không đúng về kính thiên văn?
-
A.
Gồm hai thấu kính đồng trục, thị kính có tiêu cự rất dài, vật kính là kính lúp để quan sát ảnh tạo bởi thị kính.
-
B.
Gồm hai thấu kính đồng trục, vật kính có tiêu cự rất dài, thị kính là kính lúp để quan sát ảnh tạo bởi vật kính.
-
C.
Khoảng cách giữa hai kính thay đổi được.
-
D.
Bổ trợ cho mắt khi quan sát vật ở xa bằng cách tạo ảnh ảo với góc trông rất lớn đối với vật ở xa.
Khi tính số bội giác của kính thiên văn, góc \({\alpha _0}\) được chọn là:
-
A.
góc trông trực tiếp vật đặt tại điểm cực cận của mắt.
-
B.
góc trông trực tiếp vật đặt tại điểm cực viễn của mắt cận.
-
C.
góc trông ảnh của vật ở điểm cực cận của mắt.
-
D.
góc trông trực tiếp vật.
Khi ngắm chừng vô cực một vật ở xa bằng kính thiên văn, đáp án nào sau đây sai?
-
A.
Khoảng cách hai kính là \({O_1}{O_2} = {f_1} + {f_2}\)
-
B.
Khoảng cách hai kính là \({O_1}{O_2} = {f_1} - {f_2}\)
-
C.
Số bội giác vô cực của kính là \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
-
D.
Góc trông ảnh là \(\alpha = \frac{{{f_1}}}{{{f_2}}}{\alpha _0}\)
Một kính thiên văn, vật kính có tiêu cự \({f_1} = 10m\), thị kính có tiêu cự \(5{\rm{ }}cm\). Người quan sát mắt bình thường, ngắm chừng không điều tiết. Số bội giác vô cực của kính thiên văn này là:
-
A.
200
-
B.
20
-
C.
2
-
D.
201
Một kính thiên văn, vật kính có tiêu cự \({f_1} = 1m\), thị kính có ghi \(10{\rm{x}}\). Khi ngắm chừng vô cực, khoảng cách giữa hai kính là:
-
A.
1002.5 cm
-
B.
110 cm
-
C.
102.5 cm
-
D.
105 cm
Một kính thiên văn có số bội giác vô cực là 100. Khoảng cách hai kính là 505 cm. Tiêu cự vật kính và thị kính tương ứng là
-
A.
100 cm; 1 cm.
-
B.
500cm; 5cm
-
C.
200cm; 2cm
-
D.
50cm; 0,5cm.
Một người cận thị có cực viễn cách mắt 50 cm, quan sát một thiên thể bằng kính thiên văn \(\left( {{f_1} = 100cm;{\rm{ }}{f_2} = 5{\rm{ }}cm} \right)\) không điều tiết. Biết mắt đặt sát thị kính, khoảng cách giữa hai kính lúc này bằng bao nhiêu?
-
A.
100cm
-
B.
150cm
-
C.
104,55cm
-
D.
155cm
Vật kính của một kính thiên văn có tiêu cự 90 cm, thị kính có tiêu cự 2,5 cm. Người quan sát có điểm cực cận cách mắt 20 cm, điểm cực viễn ở vô cực, đặt mắt sát thị kính để quan sát một chòm sao. Tính khoảng cách giữa vật kính và thị kính khi ngắm chừng ở cực cận?
-
A.
112,5cm
-
B.
92,5cm
-
C.
90cm
-
D.
92,2cm
Một kính thiên văn có vật kính với độ tụ 0,5dp. Thị kính cho phép nhìn một vật cao 1mm đặt tại tiêu diện vật dưới một góc \(\varphi = 0,05{\rm{r}}a{\rm{d}}\).
Tìm tiêu cự của thị kính?
-
A.
2 cm
-
B.
200 cm
-
C.
10 cm
-
D.
100 cm
Số bội giác của kính thiên văn khi ngắm chừng ở vô cực là:
-
A.
10
-
B.
200
-
C.
100
-
D.
50
Tính khoảng cách giữa hai điểm trên Mặt Trăng, nếu góc trông hai điểm này qua kính là \(4'\). Coi khoảng cách từ Trái Đất đến Mặt Trăng là \(400000km\)?
-
A.
16000km
-
B.
4,65m
-
C.
4,65km
-
D.
16000m
Vật kính của một kính thiên văn là một thấu kính hội tụ có tiêu cự lớn, thị kính là một thấu kính hội tụ có tiêu cự nhỏ. Một người, mắt không có tật, dùng kính thiên văn này để quan sát Mặt Trăng ở trạng thái không điều tiết. Khi đó, khoảng cách giữa vật kính và thị kính là 90cm. Số bội giác của kính là 17. Tiêu cự của vật kính và thị kính có giá trị là bao nhiêu? Coi mắt đặt sát kính.
-
A.
\(\left\{ \begin{array}{l}{f_1} = 85cm\\{f_2} = 5cm\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}{f_1} = 100cm\\{f_2} = 5cm\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}{f_1} = 17cm\\{f_2} = 2cm\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}{f_1} = 90cm\\{f_2} = 17cm\end{array} \right.\)
Một kính thiên văn khúc xạ được điều chỉnh cho một nguời có mắt bình thường nhìn được rõ nét của một vật ở vô cực mà không phải điều tiết. Khi đó, khoảng cách giữa vật kính và thị kính là 62cm và số bội giác của kính là 30. Vật quan sát Mặt Trăng có góc trông \({\alpha _0} = \frac{1}{{100}}ra{\rm{d}}\). Đường kính của mặt trăng cho bởi vật kính là:
-
A.
0,6cm
-
B.
1cm
-
C.
3cm
-
D.
0,9cm
Vật kính của một kính thiên văn là một thấu kính hội tụ có tiêu cự lớn; thị kính là một thấu kính hội tụ có tiêu cự nhỏ. Một người, mắt không có tật, dùng kính thiên văn này để quan sát Mặt Trăng ở trạng thái không điều tiết. Khi đó khoảng cách giữa vật kính và thị kính là 90cm. Số bội giác của kính là 17. Tính các tiêu cực của vật kính và thị kính?
-
A.
\({f_1} = 82cm;{f_2} = 8cm\)
-
B.
\({f_1} = 75cm;{f_2} = 15cm\)
-
C.
\({f_1} = 85cm;{f_2} = 5cm\)
-
D.
\({f_1} = 80cm;{f_2} = 10cm\)
Vật kính của một kính thiên văn dùng ở trường học có tiêu cự f1 = 1,2m. Thị kính là một thấu kính hội tụ có tiêu cự f2 = 4cm. Tính khoảng cách giữa hai kính và số bội giác của kính thiên văn khi ngắm chừng ở vô cực.
-
A.
\({O_1}{O_2} = 1,16m;{G_\infty } = \dfrac{1}{{30}}\)
-
B.
\({O_1}{O_2} = 1,24m;{G_\infty } = \dfrac{1}{{30}}\)
-
C.
\({O_1}{O_2} = 1,16m;{G_\infty } = 30\)
-
D.
\({O_1}{O_2} = 1,24m;{G_\infty } = 30\)
Một kính thiên văn gồm vật kính có tiêu cự f1 = 120cm và thị kính có tiêu cự f2 = 5cm. Khoảng cách giữa hai kính khi người mắt tốt quan sát Mặt Trăng trong trạng thái không điều tiết là
-
A.
125cm
-
B.
124cm
-
C.
120cm
-
D.
115cm
Lời giải và đáp án
Người ta dùng kính thiên văn để quan sát những
-
A.
vật rất nhỏ ở gần
-
B.
vật nhỏ ở ngang trước vật kính
-
C.
thiên thể ở xa
-
D.
ngôi nhà cao tầng
Đáp án : C
Người ta dùng kính thiên văn để quan sát những vật ở rất xa
Khi nói về cách sử dụng kính thiên văn, phát biểu nào sau đây đúng?
-
A.
Điều chỉnh khoảng cách giữa vật và vật kính sao cho ảnh của vật qua kính nằm trong khoảng nhìn rõ của mắt
-
B.
Điều chỉnh khoảng cách giữa vật kính và thị kính sao cho ảnh của vật qua kính nằm trong khoảng nhìn rõ của mắt
-
C.
Giữ nguyên khoảng cách giữa vật kính và thị kính, thay đổi khoảng cách giữa kính với vật sao cho ảnh của vật qua kính nằm trong khoảng nhìn rõ của mắt
-
D.
Giữ nguyên khoảng cách giữa vật kính và thị kính, thay đổi khoảng cách giữa mắt và thị kính sao cho ảnh của vật qua kính nằm trong khoảng nhìn rõ của mắt
Đáp án : B
Ngắm chừng qua kính thiên văn:
+ Điều chỉnh khoảng cách giữa thị kính với vật kính để ảnh \({A_2}{B_2}\) ảo. Tức là \({O_1}{O_2} \le {f_1} + {\rm{ }}{f_2}\)
+ Mắt đặt sau thị kính quan sát ảnh ảo A2B2 của A1B1 tạo bởi thị kính.
+ Điều chỉnh vị trí \({O_2}\) để ảnh \({A_2}{B_2}\) rơi vào khoảng nhìn rõ của mắt.
Khi nói về cấu tạo của lăng kính thiên văn, phát biểu nào sau đây là đúng?
-
A.
Vật kính là thấu kính phân kì có tiêu cự rất ngắn, thị kính là thấu kính hội tụ có tiêu cự ngắn
-
B.
Vật kính là thấu kính hội tụ có tiêu cự rất ngắn, thị kính là thấu kính phân kì có tiêu cự ngắn
-
C.
Vật kính là thấu kính hội tụ có tiêu cự dài, thị kính là thấu kính hội tụ có tiêu cự ngắn
-
D.
Vật kính là thấu kính phân kì có tiêu cự dài, thị kính là thấu kính phân kì có tiêu cự ngắn
Đáp án : C
Ta có, cấu tạo của kính thiên văn:
+ Vật kính là thấu kính hội tụ có tiêu cự lớn (có thể tới hàng chục mét).
+ Thị kính là một kính lúp để quan sát ảnh tạo bởi vật kính.
Người ta điều chỉnh kính thiên văn theo cách nào sau đây?
-
A.
Thay đổi khoảng cách giữa vật kính và thị kính bằng cách giữ nguyên vật kính, dịch chuyển thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất
-
B.
Thay đổi khoảng cách giữa vật kính và thị kính bằng cách dịch chuyển thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất
-
C.
Thay đổi khoảng cách giữa vật kính và thị kính bằng cách giữ nguyên thị kính, dịch chuyển vật kính sao cho nhìn thấy ảnh của vật to và rõ nhất
-
D.
Dịch chuyển thích hợp cả vật kính và thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất
Đáp án : A
Ta điều chỉnh kính thiên văn bằng cách thay đổi khoảng cách giữa vật kính và thị kính bằng cách giữ nguyên vật kính và di chuyển thị kính sao cho nhìn thấy ảnh của vật to và rõ.
Dùng kính thiên văn gồm vật kính và thị kính là thấu kính hội tụ có tiêu cự tương ứng là \({f_1}\) và \({f_2}\). Một người sử dụng kính này ngắm chừng ở vô cực thì khoảng cách giữa vật kính và thị kính là:
-
A.
\(\frac{{{f_1}{f_2}}}{{{f_1} + {f_2}}}\)
-
B.
\({f_1} - {f_2}\)
-
C.
\(\frac{{{f_1}{f_2}}}{{{f_1} - {f_2}}}\)
-
D.
\({f_1} + {f_2}\)
Đáp án : D
Ta có, khi ngắm chừng ở vô cực:
![]()
Dùng kính thiên văn gồm vật kính và thị kính là thấu kính hội tụ có tiêu cự tương ứng là \({f_1}\) và \({f_2}\). Khoảng cách giữa hai tiêu điểm chính gần nhất của hai thấu kính là \(\delta \). Người sử dụng kính có điểm cực cận cách mắt đoạn \(O{C_c} = Đ\). Ảnh của vật qua vật kính có số phóng đại \({k_1}\). Số bội giác của kính này khi ngắm chừng ở vô cực được tính theo công thức:
-
A.
${G_\infty } = \frac{Đ}{{{f_2}}}$
-
B.
\({G_\infty } = {k_1}{G_{2\infty }}\)
-
C.
${G_\infty } = \frac{{\delta }}{{{f_1}{f_2}}}$
-
D.
\({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
Đáp án : D
Biểu thức xác định số bội giác của kính thiên vằn khi ngắm chừng ở vô cực:
\({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
Ý kiến nào sau đây không đúng về kính thiên văn?
-
A.
Gồm hai thấu kính đồng trục, thị kính có tiêu cự rất dài, vật kính là kính lúp để quan sát ảnh tạo bởi thị kính.
-
B.
Gồm hai thấu kính đồng trục, vật kính có tiêu cự rất dài, thị kính là kính lúp để quan sát ảnh tạo bởi vật kính.
-
C.
Khoảng cách giữa hai kính thay đổi được.
-
D.
Bổ trợ cho mắt khi quan sát vật ở xa bằng cách tạo ảnh ảo với góc trông rất lớn đối với vật ở xa.
Đáp án : A
A - sai vì thị kính là kính lúp để quan sát ảnh tạo bởi vật kính và vật kính là thấu kính hội tụ có tiêu cự lớn (có thể tới hàng chục mét)
B, C, D - đúng
Khi tính số bội giác của kính thiên văn, góc \({\alpha _0}\) được chọn là:
-
A.
góc trông trực tiếp vật đặt tại điểm cực cận của mắt.
-
B.
góc trông trực tiếp vật đặt tại điểm cực viễn của mắt cận.
-
C.
góc trông ảnh của vật ở điểm cực cận của mắt.
-
D.
góc trông trực tiếp vật.
Đáp án : D
\({\alpha _0} = \tan {\alpha _0} = \frac{{{A_1}{B_1}}}{{{f_1}}}\): góc trông trực tiếp vật
Khi ngắm chừng vô cực một vật ở xa bằng kính thiên văn, đáp án nào sau đây sai?
-
A.
Khoảng cách hai kính là \({O_1}{O_2} = {f_1} + {f_2}\)
-
B.
Khoảng cách hai kính là \({O_1}{O_2} = {f_1} - {f_2}\)
-
C.
Số bội giác vô cực của kính là \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
-
D.
Góc trông ảnh là \(\alpha = \frac{{{f_1}}}{{{f_2}}}{\alpha _0}\)
Đáp án : B
A, C, D - đúng
B - sai vì: khi ngắm chừng ở vô cực thì khoảng cách hai kính là \({O_1}{O_2} = {f_1} + {f_2}\)
Một kính thiên văn, vật kính có tiêu cự \({f_1} = 10m\), thị kính có tiêu cự \(5{\rm{ }}cm\). Người quan sát mắt bình thường, ngắm chừng không điều tiết. Số bội giác vô cực của kính thiên văn này là:
-
A.
200
-
B.
20
-
C.
2
-
D.
201
Đáp án : A
Sử dụng biểu thức xác định số bội giác: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
Ta có,
+ Tiêu cự của vật kính: \({f_1} = 10m\)
+ Tiêu cự của thị kính: \({f_2} = 5cm\)
=> Số bội giác của kính thiên văn: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}} = \frac{{10}}{{0,05}} = 200\)
Một kính thiên văn, vật kính có tiêu cự \({f_1} = 1m\), thị kính có ghi \(10{\rm{x}}\). Khi ngắm chừng vô cực, khoảng cách giữa hai kính là:
-
A.
1002.5 cm
-
B.
110 cm
-
C.
102.5 cm
-
D.
105 cm
Đáp án : C
+ Cách đọc thông số trên thị kính (kính lúp): \(A{\rm{x}} = \frac{{25}}{f}\)
+ Áp dụng biểu thức khoảng cách giữa hai kính khi ngắm chừng ở vô cực: \({O_1}{O_2} = {f_1} + {f_2}\)
Ta có:
+ Tiêu cự của vật kính: \({f_1} = 1m\)
Tiêu cự của thị kính: \(10{\rm{x}} = \frac{{25}}{{{f_2}}} \to {f_2} = \frac{{25}}{{10}} = 2,5cm = 0,025m\)
+ Khoảng cách giữa hai kính khi ngắm chừng ở vô cực là: \({O_1}{O_2} = {f_1} + {f_2} = 1 + 0,025 = 1,025m = 102,5cm\)
Một kính thiên văn có số bội giác vô cực là 100. Khoảng cách hai kính là 505 cm. Tiêu cự vật kính và thị kính tương ứng là
-
A.
100 cm; 1 cm.
-
B.
500cm; 5cm
-
C.
200cm; 2cm
-
D.
50cm; 0,5cm.
Đáp án : B
Sử dụng các công thức khi ngắm chừng ở vô cực
+ Số bội giác: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
+ Khoảng cách giữa hai kính: \({O_1}{O_2} = {f_1} + {f_2}\)
Theo đề bài, ta có: \(\left\{ \begin{array}{l}{G_\infty } = \frac{{{f_1}}}{{{f_2}}} = 100\\{O_1}{O_2} = {f_1} + {f_2} = 505\end{array} \right. \to \left\{ \begin{array}{l}{f_1} = 500cm\\{f_2} = 5cm\end{array} \right.\)
Một người cận thị có cực viễn cách mắt 50 cm, quan sát một thiên thể bằng kính thiên văn \(\left( {{f_1} = 100cm;{\rm{ }}{f_2} = 5{\rm{ }}cm} \right)\) không điều tiết. Biết mắt đặt sát thị kính, khoảng cách giữa hai kính lúc này bằng bao nhiêu?
-
A.
100cm
-
B.
150cm
-
C.
104,55cm
-
D.
155cm
Đáp án : C
+ Vẽ sơ đồ tạo ảnh qua hệ thấu kính
+ Vị trí vật đối với người cận thị khi mắt không điều tiết: \({d_1} = \infty \)
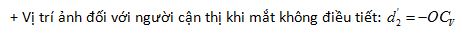
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Mắt cận nhìn thiên thể ở trạng thái không điều tiết, nghĩa là:
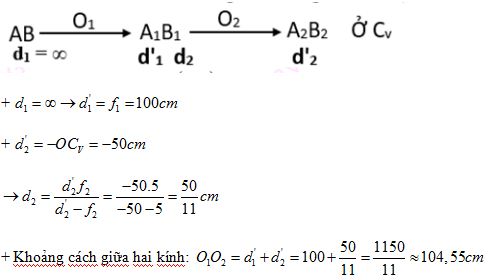
Vật kính của một kính thiên văn có tiêu cự 90 cm, thị kính có tiêu cự 2,5 cm. Người quan sát có điểm cực cận cách mắt 20 cm, điểm cực viễn ở vô cực, đặt mắt sát thị kính để quan sát một chòm sao. Tính khoảng cách giữa vật kính và thị kính khi ngắm chừng ở cực cận?
-
A.
112,5cm
-
B.
92,5cm
-
C.
90cm
-
D.
92,2cm
Đáp án : D
+ Vị trí vật: \({d_1} = \infty \)
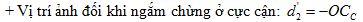
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)
Ta có:
+ Khi quan sát chòm sao: \({d_1} = \infty \to {d_1}' = {f_1} = 90cm\)
+ Khi ngắm chừng ở điểm cực cận:
\(\begin{array}{l}{d_2}' = - O{C_C} = - 20cm\\ \to {d_2} = \frac{{{d_2}'{f_2}}}{{{d_2}' - {f_2}}} = \frac{{ - 20.2,5}}{{ - 20 - 2,5}} = \frac{{20}}{9}cm\end{array}\)
+ Khoảng cách giữa vật kính và thị kính: \({O_1}{O_2} = {d_1}' + {d_2} = 90 + \frac{{20}}{9} = 92,2cm\)
Một kính thiên văn có vật kính với độ tụ 0,5dp. Thị kính cho phép nhìn một vật cao 1mm đặt tại tiêu diện vật dưới một góc \(\varphi = 0,05{\rm{r}}a{\rm{d}}\).
Tìm tiêu cự của thị kính?
-
A.
2 cm
-
B.
200 cm
-
C.
10 cm
-
D.
100 cm
Đáp án: A
Sử dụng công thức tính góc trông vật: \(\tan \varphi = \frac{{{A_1}{B_1}}}{{{f_2}}} \approx \varphi \)
Ta có: Vật \({A_1}{B_1}\) đặt tại tiêu diện vật \({F_2}\) của thị kính nên ảnh \({A_2}{B_2}\) ở vô cực, ta có:
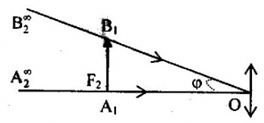
\(\begin{array}{l}\tan \varphi = \frac{{{A_1}{B_1}}}{{{f_2}}} \approx \varphi \\ \to {f_2} = \frac{{{A_1}{B_1}}}{\varphi } = \frac{{0,1}}{{0,05}} = 2cm\end{array}\)
Số bội giác của kính thiên văn khi ngắm chừng ở vô cực là:
-
A.
10
-
B.
200
-
C.
100
-
D.
50
Đáp án: C
+ Sử dụng biểu thức xác định tiêu cự: \(f = \frac{1}{D}\)
+ Áp dụng biểu thức tính số bội giác của kính thiên văn khi ngắm chừng ở vô cực: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
+ Tiêu cự của vật kính: \({f_1} = \frac{1}{{0,5}} = 2m = 200cm\)
+ Số bội giác: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}} = \frac{{200}}{2} = 100\)
Tính khoảng cách giữa hai điểm trên Mặt Trăng, nếu góc trông hai điểm này qua kính là \(4'\). Coi khoảng cách từ Trái Đất đến Mặt Trăng là \(400000km\)?
-
A.
16000km
-
B.
4,65m
-
C.
4,65km
-
D.
16000m
Đáp án: C
+ Số bội giác: \({G_\infty } = \frac{\alpha }{{{\alpha _0}}} = 100 \to {\alpha _0} = \frac{\alpha }{{100}}\)
Ta có: \(\alpha = 4' = \frac{4}{{60}}\frac{\pi }{{180}} = {1,16.10^{ - 3}}\left( {ra{\rm{d}}} \right) \to {\alpha _0} = {1,16.10^{ - 5}}\left( {ra{\rm{d}}} \right)\)
+ Mặt khác, ta có:
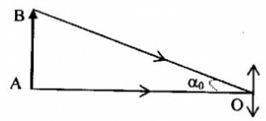
\(\begin{array}{l}\tan {\alpha _0} = \frac{{AB}}{{OA}} \approx {\alpha _0}\\ \to AB = OA.{\alpha _0} = {4.10^5}{.1,16.10^{ - 5}} = 4,65\left( {km} \right)\end{array}\)
Vật kính của một kính thiên văn là một thấu kính hội tụ có tiêu cự lớn, thị kính là một thấu kính hội tụ có tiêu cự nhỏ. Một người, mắt không có tật, dùng kính thiên văn này để quan sát Mặt Trăng ở trạng thái không điều tiết. Khi đó, khoảng cách giữa vật kính và thị kính là 90cm. Số bội giác của kính là 17. Tiêu cự của vật kính và thị kính có giá trị là bao nhiêu? Coi mắt đặt sát kính.
-
A.
\(\left\{ \begin{array}{l}{f_1} = 85cm\\{f_2} = 5cm\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}{f_1} = 100cm\\{f_2} = 5cm\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}{f_1} = 17cm\\{f_2} = 2cm\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}{f_1} = 90cm\\{f_2} = 17cm\end{array} \right.\)
Đáp án : A
+ Vẽ sơ đồ tạo ảnh qua hệ thấu kính
+ Quan sát vật ở rất xa: \({d_1} = \infty \)
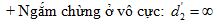
+ Sử dụng công thức tính khoảng cách giữa hai kính khi ngắm chừng ở vô cực: \({O_1}{O_2} = {f_1} + {f_2}\)
+ Sử dụng công thức tính số bội giác khi ngắm chừng ở vô cực: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
Ta có, quá trình tạo ảnh của kính thiên văn giống như quá trình tạo ảnh qua hệ hai thấu kính ghép đồng trục và được tóm tắt qua sơ đồ sau:
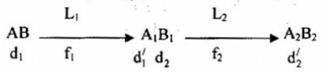

Một kính thiên văn khúc xạ được điều chỉnh cho một nguời có mắt bình thường nhìn được rõ nét của một vật ở vô cực mà không phải điều tiết. Khi đó, khoảng cách giữa vật kính và thị kính là 62cm và số bội giác của kính là 30. Vật quan sát Mặt Trăng có góc trông \({\alpha _0} = \frac{1}{{100}}ra{\rm{d}}\). Đường kính của mặt trăng cho bởi vật kính là:
-
A.
0,6cm
-
B.
1cm
-
C.
3cm
-
D.
0,9cm
Đáp án : A
+ Vẽ sơ đồ tạo ảnh qua hệ thấu kính
+ Quan sát vật ở rất xa: \({d_1} = \infty \)
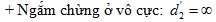
+ Sử dụng công thức tính khoảng cách giữa hai kính khi ngắm chừng ở vô cực: \({O_1}{O_2} = {f_1} + {f_2}\)
+ Sử dụng công thức tính số bội giác khi ngắm chừng ở vô cực: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
+ Vẽ hình, sử dụng công thức: \(\tan {\alpha _0} = \frac{{{A_1}{B_1}}}{{{f_1}}}\)
Ta có
+ Sơ đồ tạo ảnh qua hệ thấu kính:
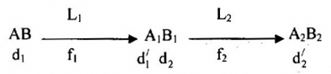
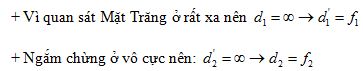
+ Khoảng cách giữa hai kính: \({O_1}{O_2} = {f_1} + {f_2} = 62cm\,\,\,\left( 1 \right)\)
+ Số bội giác của kính thiên văn khi ngắm chừng ở vô cực: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}} = 30\,\,\,\left( 2 \right)\)
Từ (1) và (2), ta suy ra: \(\left\{ \begin{array}{l}{f_1} = 60cm\\{f_2} = 2cm\end{array} \right.\)
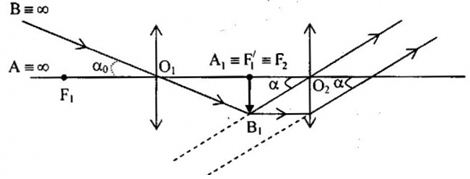
Ta có:
\(\begin{array}{l}\tan {\alpha _0} = \frac{{{A_1}{B_1}}}{{{f_1}}}\\ \to {A_1}{B_1} = {f_1}\tan {\alpha _0} \approx {f_1}.{\alpha _0} = \frac{{60}}{{100}} = 0,6\left( {cm} \right)\end{array}\)
Vật kính của một kính thiên văn là một thấu kính hội tụ có tiêu cự lớn; thị kính là một thấu kính hội tụ có tiêu cự nhỏ. Một người, mắt không có tật, dùng kính thiên văn này để quan sát Mặt Trăng ở trạng thái không điều tiết. Khi đó khoảng cách giữa vật kính và thị kính là 90cm. Số bội giác của kính là 17. Tính các tiêu cực của vật kính và thị kính?
-
A.
\({f_1} = 82cm;{f_2} = 8cm\)
-
B.
\({f_1} = 75cm;{f_2} = 15cm\)
-
C.
\({f_1} = 85cm;{f_2} = 5cm\)
-
D.
\({f_1} = 80cm;{f_2} = 10cm\)
Đáp án : C
+ Khoảng cách giữa vật kính và thấu kính của kính thiên văn ngắm chừng ở vô cực : O1O2 = f1 + f2
+ Số bội giác trong trường hợp ngắm chừng ở vô cực: \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}}\)
Nếu mắt không có tật, quan sát ảnh ở trạng thái không điều tiết thì ảnh này ở vô cực (ngắm chừng ở vô cực)
Sơ đồ tạo ảnh:
Với AB: \({d_2}' \to \infty \Rightarrow {d_2} = {f_2}\)
Với A1B1: \({d_1} \to \infty \Rightarrow {d_1}' = {f_1}\)
Ta suy ra: \({d_2} = l - {d_1}' \Rightarrow l = {f_1} + {f_2}\)
Vậy theo bài ra: \({f_1} + {f_2} = 90cm\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Mặt khác, số bội giác của kính khi ngắm chừng ở vô cực được tính bởi:
\({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}} = 17 \Rightarrow {f_1} - 17.{f_2} = 0\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}{f_1} + {f_2} = 90cm\\{f_1} - 17.{f_2} = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{f_1} = 85cm\\{f_2} = 5cm\end{array} \right.\)
Vật kính của một kính thiên văn dùng ở trường học có tiêu cự f1 = 1,2m. Thị kính là một thấu kính hội tụ có tiêu cự f2 = 4cm. Tính khoảng cách giữa hai kính và số bội giác của kính thiên văn khi ngắm chừng ở vô cực.
-
A.
\({O_1}{O_2} = 1,16m;{G_\infty } = \dfrac{1}{{30}}\)
-
B.
\({O_1}{O_2} = 1,24m;{G_\infty } = \dfrac{1}{{30}}\)
-
C.
\({O_1}{O_2} = 1,16m;{G_\infty } = 30\)
-
D.
\({O_1}{O_2} = 1,24m;{G_\infty } = 30\)
Đáp án : D
+ Khoảng cách giữa vật kính và thấu kính của kính thiên văn ngắm chừng ở vô cực : O1O2 = f1 + f2
+ Số bội giác trong trường hợp ngắm chừng ở vô cực: \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}}\)
Khi ngắm chừng ở vô cực:
+ Khoảng cách giữa hai kính: \({O_1}{O_2}\; = \;{f_1}\; + {\rm{ }}{f_2}\; = 1,2 + 0,04 = 1,24{\rm{ }}m\)
+ Số bội giác của kính thiên văn: \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}} = \dfrac{{1,2}}{{0,04}} = 30\)
Một kính thiên văn gồm vật kính có tiêu cự f1 = 120cm và thị kính có tiêu cự f2 = 5cm. Khoảng cách giữa hai kính khi người mắt tốt quan sát Mặt Trăng trong trạng thái không điều tiết là
-
A.
125cm
-
B.
124cm
-
C.
120cm
-
D.
115cm
Đáp án : A
Khoảng cách giữa hai kính của kính thiên văn khi người mắt tốt quan sát Mặt Trăng trong trạng thái không điều tiết là L = f1+ f2
Khoảng cách giữa hai kính của kính thiên văn khi người mắt tốt quan sát Mặt Trăng trong trạng thái không điều tiết là L = f1+ f2 = 120 + 5 = 125cm
Luyện tập và củng cố kiến thức Ôn tập chương 7 Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 33. Kính hiển vi Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 32. Kính lúp Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp các dạng bài tập về mắt Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 31. Mắt Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 29. Các dạng bài tập thấu kính Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập thấu kính (phần 2) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tông hợp bài tập thấu kính (phần 1) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 28. Lăng kính - Bài tập lăng kính Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết










Danh sách bình luận