Trắc nghiệm Tổng hợp bài tập định luật Culông (phần 2) - Vật Lí 11
Đề bài
Hai quả cầu giống nhau bằng kim loại khối lượng m = 5g, được treo cùng vào một điểm O bằng hai sợi dây không dãn, dài 10cm. Hai quả cầu tiếp xúc với nhau. Tích điện cho mỗi quả cầu thì thấy chúng đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 600. Tính độ lớn điện tích mà ta đã truyền cho quả cầu. Lấy g =10m/s2.
-
A.
3,58.10-7C
-
B.
2,35.10-7C
-
C.
5,38.10-7C
-
D.
3,38.10-7C
Hai quả cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5g, được treo vào cùng một điểm O bằng 2 sợi dây không dãn, dài 30cm. Hai quả cầu tiếp xúc nhau. Tích điện cho mỗi quả cầu thì thấy chúng đẩy nhau cho đến khi hai dây treo hợp nhau một góc 900. Tính độ lớn điện tích mà ta đã truyền cho quả cầu. Lấy g = 10m/s2.
-
A.
2.10-6 C
-
B.
0,5.10-7C
-
C.
2.10-7C
-
D.
4.10-6C
Hai quả cầu giống nhau, tích điện như nhau treo ở hai đầu A và B của hai sợi dây cùng độ dài OA, OB có đầu O chung được giữ cố định trong chân không. Sau đó tất cả được nhúng trong dầu hỏa (có khối lượng riêng ρ0 và hằng số số điện môi \(ε = 4\)). Biết rằng so với trường hợp trong chân không góc AOB không thay đổi và gọi \(ρ\) là khối lượng riêng của hai quả cầu. Hãy tính tỉ số ρ/ρ0. Biết hai sợi dây OA, OB không co dãn và có khối lượng không đáng kể.
-
A.
4/3
-
B.
3/4
-
C.
3/5
-
D.
5/3
Hai quả cầu nhỏ bằng kim loại giống hệt nhau được treo ở hai đầu dây có cùng chiều dài. Hai đầu kia của hai dây móc vào cùng một điểm. Cho hai quả cầu tích điện bằng nhau, lúc cân bằng chúng cách nhau r = 6,35cm. Chạm tay vào một trong hai quả cầu, hãy tính khoảng cách r’ giữa hai quả cầu sau khi chúng đạt vị trí cân bằng mới. Giả thiết chiều dài mỗi dây khá lớn so với khoảng cách hai quả cầu lúc cân bằng.
-
A.
2cm
-
B.
3cm
-
C.
4cm
-
D.
5cm
Hai quả cầu nhỏ giống nhau, mỗi quả cầu có điện tích q và khối lượng m = 10g được treo bởi hai sợi dây cùng chiều dài l = 30cm vào cùng một điểm O. Giữ quả cầu 1 cố định theo phương thẳng đứng, dây treo quả cầu 2 bị lệch góc α = 600 so với phương thẳng đứng. Cho g = 10m/s2. Tìm q
-
A.
2nC
-
B.
1pC
-
C.
2μC
-
D.
1μC
Có hai điện tích ${q_1} = {\rm{ }}q{\rm{ }} < {\rm{ }}0$ và ${q_2} = {\rm{ }}4q$ đặt cố định trong không khí cách nhau một khoảng $a{\rm{ }} = {\rm{ }}30cm$. Phải đặt một điện tích ${q_3}$ cách ${q_1}$ một khoảng $l$ bao nhiêu để nó cân bằng?
-
A.
$l = 10cm$
-
B.
$l = 20cm$
-
C.
$l = 15cm$
-
D.
$l = 35cm$
Hai điện tích điểm q1 = q2 = -4. 10-6C, đặt tại A và B cách nhau 10 cm trong không khí. Phải đặt điện tích q3 = 4. 10-8C cách A và B những khoảng r1 và r2 bằng bao nhiêu để q3 nằm cân bằng?
-
A.
r1 = 10cm, r2 = 5cm
-
B.
r1 = 5cm, r2 = 10cm
-
C.
r1 = r2 = 10cm
-
D.
r1 = r2 = 5cm
Hai điện tích \({q_1} = {\rm{ }}2.{\rm{ }}{10^{ - 8}}C\) , \({q_2} = {\rm{ }} - 8.{\rm{ }}{10^{ - 8}}C\) đặt tại A và B trong không khí, \(AB{\rm{ }} = {\rm{ }}8{\rm{ }}cm\). Một điện tích \({q_3}\) đặt tại C. Dấu và độ lớn của \({q_3}\) để \({q_1}\) và \({q_2}\) cũng cân bằng ?
-
A.
\( \pm {4.10^{ - 6}}C\)
-
B.
\( - {8.10^{ - 6}}C\)
-
C.
\({4.10^{ - 8}}C\)
-
D.
\( \pm {8.10^{ - 6}}C\)
Tại ba đỉnh của một tam giác đều, người ta đặt ba điện tích giông nhau q1 = q2 = q3 = 6.10-7 C. Cần phải đặt điện tích thứ tư q0 tại đâu, có giá trị bằng bao nhiêu để hệ thống cân bằng.
-
A.
Tâm của tam giác, q0 = - 3,46.107C
-
B.
Tâm của tam giác, q0 = 3,46.10-7C
-
C.
Tâm đường tròn ngoại tiếp, q0 = 3,46.10-7C
-
D.
Tâm đường tròn nội tiếp, q0 = 3,46.10-7C
Bốn điện tích q = 3.10-7C giống nhau đặt tại 4 đỉnh của hình vuông. Phải đặt một điện tích q0 nằm ở đâu và bằng bao nhiêu để năm điện tích này cân bằng
-
A.
Tâm hình hình vuông, q0 = -2,87.10-7C
-
B.
1 đỉnh hình vuông, q0 = 2,87.10-7C
-
C.
Tâm hình vuông, q0 = 2,87.10-7C
-
D.
1 đỉnh hình vuông, q0 = -2,87.10-7C
Một quả cầu khối lượng \(m = 4g\) treo bằng một sợi chỉ mảnh. Điện tích của quả cầu là \({q_1} = {2.10^{ - 8}}C\). Phía dưới quả cầu dọc theo phương của sợi chỉ có một điện tích \({q_2}\). Khoảng cách giữa hai điện tích là \(r = 5cm\) và lực căng dây là \(T = {5.10^{ - 2}}N\). Xác định điện tích \({q_2}\) và lực tác dụng giữa chúng, lấy \(g = 10m/{s^2}\)
-
A.
\({q_2} = - 1,{39.10^{ - 7}}C\)
-
B.
\({q_2} = 1,{39.10^{ - 7}}C\)
-
C.
\({q_2} = 1,{25.10^{ - 6}}C\)
-
D.
\({q_2} = - 1,{25.10^{ - 6}}C\)
Hai quả cầu nhỏ giống hệt nhau bằng kim loại A và B đặt trong không khí, có điện tích lần lượt là q1 = -3,2.10-7 C, q2 = 2,4.10-7 C, cách nhau một khoảng 12 cm. Xác định số electron thừa và thiếu ở mỗi quả cầu?
-
A.
Số electron thiếu ở quả cầu A là 2.1012 electron. Số electron thừa ở quả cầu B là 1,5.1012 electron
-
B.
Số electron thừa ở quả cầu A là 1,5.1012 electron. Số electron thiếu ở quả cầu B là 2.1012 electron
-
C.
Số electron thừa ở quả cầu A là 2.1012 electron. Số electron thiếu ở quả cầu B là 1,5.1012 electron
-
D.
Số electron thiếu ở quả cầu A là 1,5.1012 electron. Số electron thừa ở quả cầu B là 2.1012 electron
Cho hai quả cầu kim loại nhỏ, giống nhau, tích điện và cách nhau 20 cm thì chúng hút nhau một lực bằng 1,2 N. Cho chúng tiếp xúc với nhau rồi tách chúng ra đến khoảng cách như cũ thì chúng đẩy nhau một lực bằng lực hút. Tính điện tích lúc đầu của mỗi quả cầu
-
A.
\({q_1} = 0,{96.10^{ - 6}}C;{q_2} = - 5,{58.10^{ - 6}}C\)
-
B.
\({q_1} = - 5,{58.10^{ - 6}}C;{q_2} = 0,{96.10^{ - 6}}C\)
-
C.
Một kết quả khác
-
D.
A hoặc B
Cho hai loại điện tích q1và q2 đặt cách nhau 15cm trong không khí, lực tác dụng giữa chúng là F. Khi đặt chúng trong dầu thì lực này còn bằng F/2,25. Để lực tác dụng vẫn là F thì cần phải dịch chuyển chúng lại một đoạn là
-
A.
5cm
-
B.
10cm
-
C.
6cm
-
D.
8cm
Cho 4 điện tích \({q_{1\;}} = {q_{3\;}} = {4.10^{ - 6}}C;{q_{2\;}} = {q_4} = - {4.10^{ - 6}}C\) giống nhau đặt tại 4 đỉnh của hình vuông ABCD cạnh 10cm theo thứ tự A, B, C, D. Tìm lực điện tác dụng lên \({q_0} = - {2.10^{ - 6}}C\) đặt tại tâm O của hình vuông.
-
A.
\(4,{2.10^{ - 4}}N\)
-
B.
\(2,{1.10^{ - 4}}N\)
-
C.
\(8,{4.10^{ - 4}}N\)
-
D.
\(0N\)
Cho 4 điện tích \({q_{1\;}} = {q_{2\;}} = {q_{3\;}} = {q_4} = - {2.10^{ - 8}}C\) lần lượt đặt tại 4 đỉnh của hình vuông ABCD cạnh 4cm theo thứ tự A, B, C, D. Tìm lực điện tổng hợp tác dụng lên điện tích đặt tại D?
-
A.
\(2,{31.10^{ - 3}}N\)
-
B.
\(2,{06.10^{ - 3}}N\)
-
C.
\(4,{06.10^{ - 3}}N\)
-
D.
\(4,{31.10^{ - 3}}N\)
Người ta treo hai quả cầu nhỏ khối lượng bằng nhau m = 0,1g bằng hai sợi dây nhę có độ dài l = 1,5m như nhau. Cho chúng nhiễm điện bằng nhau thì chúng đẩy nhau và cân bằng khi mỗi dây treo hợp với phương thẳng đứng một góc \({15^0}\). Tính độ lớn điện tích tích cho mỗi quả cầu. Lấy \(g = 10m/{s^2}\)
-
A.
\(178,{63.10^{ - 9}}{\rm{C}}\)
-
B.
\(103,{5.10^{ - 5}}{\rm{C}}\)
-
C.
\(89,{32.10^{ - 9}}{\rm{C}}\)
-
D.
\(133,{97.10^{ - 9}}{\rm{C}}\)
Hai điện tích điểm bằng nhau đặt trong không khí cách nhau 12cm, lực tương tác giữa chúng bằng 40N. Các điện tích đó bằng:
-
A.
\( \pm 12\mu {\rm{C}}\)
-
B.
\( \pm 8\mu {\rm{C}}\)
-
C.
\( \pm 4\mu {\rm{C}}\)
-
D.
\( \pm 5\mu {\rm{C}}\)
Lời giải và đáp án
Hai quả cầu giống nhau bằng kim loại khối lượng m = 5g, được treo cùng vào một điểm O bằng hai sợi dây không dãn, dài 10cm. Hai quả cầu tiếp xúc với nhau. Tích điện cho mỗi quả cầu thì thấy chúng đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 600. Tính độ lớn điện tích mà ta đã truyền cho quả cầu. Lấy g =10m/s2.
-
A.
3,58.10-7C
-
B.
2,35.10-7C
-
C.
5,38.10-7C
-
D.
3,38.10-7C
Đáp án : A
+ Áp dụng phương pháp giải bài toán con lắc tích điện
+ Vận dụng công thức lượng giác
+ Áp dụng công thức tính lực tương tác điện tích: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
Ta có:
- Các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \), lực căng dây \(\overrightarrow T \), lực tương tác tĩnh điện (lực tĩnh điện) \(\overrightarrow F \)giữa hai quả cầu.
- Khi quả cầu cân bằng, ta có:
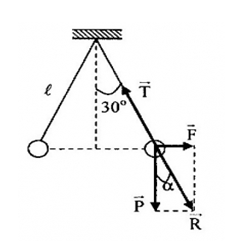
\(\overrightarrow T + \overrightarrow P + \overrightarrow F = 0 \leftrightarrow \overrightarrow T + \overrightarrow R = 0\)
=> \(\overrightarrow R \)cùng phương, ngược chiều với \(\overrightarrow T \)\( \to \alpha = {30^0}\)
Ta có: \(\tan {30^0} = \frac{F}{P} \to F = P\tan {30^0} = mg\tan {30^0} = 0,029N\)
- Mặt khác, ta có:
\[\left\{ \begin{array}{l}F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_2}} \right| = \left| q \right|\\\sin {30^0} = \frac{{\frac{r}{2}}}{l} \to r = 2l\sin {30^0} = l\end{array} \right. \to F = k\frac{{{q^2}}}{{{l^2}}} \to \left| q \right| = 1,{79.10^{ - 7}}C\]
=> Tổng độ lớn điện tích đã truyền cho hai quả cầu là:
Q = 2|q| = 3,58.10-7C
Hai quả cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5g, được treo vào cùng một điểm O bằng 2 sợi dây không dãn, dài 30cm. Hai quả cầu tiếp xúc nhau. Tích điện cho mỗi quả cầu thì thấy chúng đẩy nhau cho đến khi hai dây treo hợp nhau một góc 900. Tính độ lớn điện tích mà ta đã truyền cho quả cầu. Lấy g = 10m/s2.
-
A.
2.10-6 C
-
B.
0,5.10-7C
-
C.
2.10-7C
-
D.
4.10-6C
Đáp án : A
+ Áp dụng phương pháp giải bài toán con lắc tích điện
+ Vận dụng công thức lượng giác
+ Áp dụng công thức tính lực tương tác điện tích: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
- Các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \), lực căng dây \(\overrightarrow T \), lực tương tác tĩnh điện (lực tĩnh điện) \(\overrightarrow F \)giữa hai quả cầu.
- Khi quả cầu cân bằng, ta có:
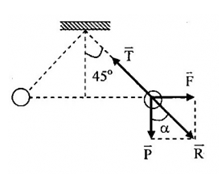
\(\overrightarrow T + \overrightarrow P + \overrightarrow F = 0 \leftrightarrow \overrightarrow T + \overrightarrow R = 0\)
=> \(\overrightarrow R \)cùng phương, ngược chiều với \(\overrightarrow T \)\( \to \alpha = {45^0}\)
Ta có: \(\tan {45^0} = \frac{F}{P} \to F = P = mg = 0,05N\)
- Mặt khác, ta có:
\(\left\{ \begin{array}{l}F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_2}} \right| = \left| q \right|\end{array} \right. \to F = k\frac{{{q^2}}}{{{r^2}}}\)
- Từ hình ta có: \(r = 2(l\sin {45^0}) = l\sqrt 2 \)
\( \to F = k\frac{{{q^2}}}{{{r^2}}} = k\frac{{{q^2}}}{{2{l^2}}} \to \left| q \right| = l\sqrt {\frac{{2F}}{k}} = {10^{ - 6}}C\)
=> Tổng độ lớn điện tích đã truyền cho hai quả cầu là:
Q = 2|q| = 2.10-6C
Hai quả cầu giống nhau, tích điện như nhau treo ở hai đầu A và B của hai sợi dây cùng độ dài OA, OB có đầu O chung được giữ cố định trong chân không. Sau đó tất cả được nhúng trong dầu hỏa (có khối lượng riêng ρ0 và hằng số số điện môi \(ε = 4\)). Biết rằng so với trường hợp trong chân không góc AOB không thay đổi và gọi \(ρ\) là khối lượng riêng của hai quả cầu. Hãy tính tỉ số ρ/ρ0. Biết hai sợi dây OA, OB không co dãn và có khối lượng không đáng kể.
-
A.
4/3
-
B.
3/4
-
C.
3/5
-
D.
5/3
Đáp án : A
+ Áp dụng phương pháp giải bài toán con lắc tích điện
+ Vận dụng công thức lượng giác
+ Áp dụng công thức tính lực tương tác điện tích: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
+ Vận dụng biểu thức \(m = ρVg\)
- Ở trong chân không các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \), lực căng dây \({\overrightarrow T _1}\), lực tương tác tĩnh điện (lực tĩnh điện) \(\overrightarrow F \)giữa hai quả cầu.
- Ở trong dầu hỏa các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \), lực căng dây \(\overrightarrow {{T_2}} \), lực tương tác tĩnh điện (lực tĩnh điện) \(\overrightarrow {{F_2}} \) giữa hai quả cầu, lực đẩy acsimet \(\overrightarrow {{F_A}} \)
Các lực tác dụng lên quả cầu trong mỗi trường hợp được biểu diễn như hình:
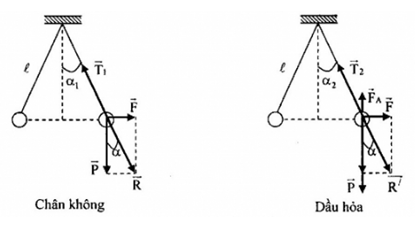
Vì góc AOB không thay đổi nên:
\(\begin{array}{l}\tan {\alpha _1} = \tan {\alpha _2} \leftrightarrow \dfrac{{{F_1}}}{P} = \dfrac{{{F_2}}}{{P - {F_A}}}\\ \leftrightarrow k\dfrac{{{q^2}}}{{{r^2}P}} = k\dfrac{{{q^2}}}{{\varepsilon {r^2}(P - {F_A})}} \to \varepsilon {F_A} = P(\varepsilon - 1)\\ \to \varepsilon {\rho _0}Vg = mg(\varepsilon - 1) = \rho Vg(\varepsilon - 1)\\ \to \dfrac{\rho }{{{\rho _0}}} = \dfrac{\varepsilon }{{\varepsilon - 1}} = \dfrac{4}{3}\end{array}\)
Hai quả cầu nhỏ bằng kim loại giống hệt nhau được treo ở hai đầu dây có cùng chiều dài. Hai đầu kia của hai dây móc vào cùng một điểm. Cho hai quả cầu tích điện bằng nhau, lúc cân bằng chúng cách nhau r = 6,35cm. Chạm tay vào một trong hai quả cầu, hãy tính khoảng cách r’ giữa hai quả cầu sau khi chúng đạt vị trí cân bằng mới. Giả thiết chiều dài mỗi dây khá lớn so với khoảng cách hai quả cầu lúc cân bằng.
-
A.
2cm
-
B.
3cm
-
C.
4cm
-
D.
5cm
Đáp án : C
+ Áp dụng phương pháp giải bài toán con lắc tích điện
+ Vận dụng công thức lượng giác
+ Áp dụng công thức tính lực tương tác điện tích: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
+ Áp dụng công thức tính giá trị gần đúng
- Các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \), lực căng dây \(\overrightarrow T \), lực tương tác tĩnh điện\(\overrightarrow F \).
- Khi quả cầu cân bằng, ta có:
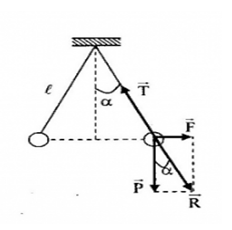
\(\overrightarrow T + \overrightarrow P + \overrightarrow F = 0 \leftrightarrow \overrightarrow T + \overrightarrow R = 0\)
=> \(\overrightarrow R \)cùng phương, ngược chiều với \(\overrightarrow T \)
Ta có: \(\tan \alpha = \frac{F}{P} = \frac{{\frac{r}{2}}}{{\sqrt {{l^2} - {{\left( {\frac{r}{2}} \right)}^2}} }} \to F = P\frac{{\frac{r}{2}}}{{\sqrt {{l^2} - {{\left( {\frac{r}{2}} \right)}^2}} }}\)
+ Ta có:
\(\begin{array}{l}{l^2} \gg {\left( {\frac{r}{2}} \right)^2} \to {l^2} - {\left( {\frac{r}{2}} \right)^2} \approx {l^2}\\ \to \sqrt {{l^2} - {{\left( {\frac{r}{2}} \right)}^2}} \approx l \to F \approx \frac{{P{\rm{r}}}}{{2l}}\end{array}\)
+ Lúc đầu: \({F_1} = k\frac{{{q^2}}}{{{r^2}}} = \frac{{\Pr }}{{2l}}\) (1)
+ Giả sử ta chạm tay vào quả 1, kết quả sau đó quả cầu 1 sẽ mất điện tích, lúc đó giữa hai quả cầu không còn lực tương tác nên chúng sẽ trở về vị trí dây treo thẳng đứng.
+ Khi chúng vừa chạm vào nhau thì điện tích của quả 2 sẽ truyền sang quả 1 và lúc này điện tích mỗi quả sẽ là:
\({q_1}' = {q_2}' = \frac{{{q_2}}}{2} = \frac{q}{2} \to {F_2} = k\frac{{{q^2}}}{{4.r{'^2}}}{\rm{ = }}\frac{{P{\rm{r}}'}}{{2l}}{\rm{ (2)}}\)
Từ (1) và (2) ta có:
\(\frac{{{F_1}}}{{{F_2}}} = \frac{{k\frac{{{q^2}}}{{{r^2}}}}}{{k\frac{{{q^2}}}{{4.r{'^2}}}}} = \frac{{\frac{{\Pr }}{{2l}}}}{{\frac{{P{\rm{r}}'}}{{2l}}}} \leftrightarrow \frac{{4r{'^2}}}{{{r^2}}} = \frac{r}{{r'}} \leftrightarrow 4{\rm{r}}{'^3} = {r^3} \to r' = \frac{r}{{\sqrt(3){4}}} = \frac{{6,35}}{{\sqrt(3){4}}} \approx 4cm\)
Hai quả cầu nhỏ giống nhau, mỗi quả cầu có điện tích q và khối lượng m = 10g được treo bởi hai sợi dây cùng chiều dài l = 30cm vào cùng một điểm O. Giữ quả cầu 1 cố định theo phương thẳng đứng, dây treo quả cầu 2 bị lệch góc α = 600 so với phương thẳng đứng. Cho g = 10m/s2. Tìm q
-
A.
2nC
-
B.
1pC
-
C.
2μC
-
D.
1μC
Đáp án : D
+ Áp dụng phương pháp giải bài toán con lắc tích điện
+ Vận dụng công thức lượng giác
+ Áp dụng công thức tính lực tương tác điện tích: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
- Các lực tác dụng lên quả cầu gồm: Trọng lực \(\overrightarrow P \), lực căng dây \(\overrightarrow T \), lực tương tác tĩnh điện\(\overrightarrow F \).
- Khi quả cầu cân bằng, ta có:
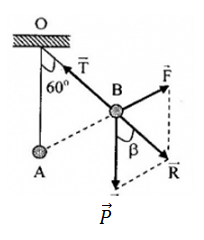
\(\overrightarrow T + \overrightarrow P + \overrightarrow F = 0 \leftrightarrow \overrightarrow T + \overrightarrow R = 0\)
=> \(\overrightarrow R \)cùng phương, ngược chiều với \(\overrightarrow T \)
=> β = 600
=> Tam giác BPR là tam giác đều
\( \to F = P \leftrightarrow k\frac{{{q^2}}}{{{l^2}}} = mg \to \left| q \right| = l\sqrt {\frac{{mg}}{k}} = {10^{ - 6}}C\)
Có hai điện tích ${q_1} = {\rm{ }}q{\rm{ }} < {\rm{ }}0$ và ${q_2} = {\rm{ }}4q$ đặt cố định trong không khí cách nhau một khoảng $a{\rm{ }} = {\rm{ }}30cm$. Phải đặt một điện tích ${q_3}$ cách ${q_1}$ một khoảng $l$ bao nhiêu để nó cân bằng?
-
A.
$l = 10cm$
-
B.
$l = 20cm$
-
C.
$l = 15cm$
-
D.
$l = 35cm$
Đáp án : A
+ Áp dụng biểu thức định luật Cu-lông: $F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}$
+ Vận dụng phương pháp tổng hợp lực
+ Vận dụng điều kiện cân bằng của vật
- Gọi:
+ A, B, C lần lượt là các điểm đặt q1, q2, q3
+ \(\overrightarrow {{F_{10}}} ,\overrightarrow {{F_{20}}} \) lần lượt là lực do q1, q2 tác dụng lên q3
- Điều kiện cân bằng của q0: \(\overrightarrow {{F_{10}}} + \overrightarrow {{F_{20}}} = 0 \to \overrightarrow {{F_{10}}} = - \overrightarrow {{F_{20}}} \)
- Vì ${q_1}$ và ${q_2}$ cùng dấu => ${q_3}$ phải nằm trong AB
=> Điểm C phải thuộc AB
Lại có:
\(\begin{array}{l}{F_{10}} = {F_{20}} \to k\dfrac{{{q_1}{q_0}}}{{C{A^2}}} = k\dfrac{{{q_2}{q_0}}}{{C{B^2}}}\\ \leftrightarrow \dfrac{{{q_1}}}{{C{A^2}}} = \dfrac{{{q_2}}}{{C{B^2}}}\\ \to \dfrac{{CB}}{{CA}} = 2\\ \to CB = 2CA\end{array}\)

Lại có: $CA{\rm{ }} + {\rm{ }}CB{\rm{ }} = {\rm{ }}30cm$
=> $CA{\rm{ }} = {\rm{ }}10cm$ và $CB{\rm{ }} = {\rm{ }}20cm$
Hai điện tích điểm q1 = q2 = -4. 10-6C, đặt tại A và B cách nhau 10 cm trong không khí. Phải đặt điện tích q3 = 4. 10-8C cách A và B những khoảng r1 và r2 bằng bao nhiêu để q3 nằm cân bằng?
-
A.
r1 = 10cm, r2 = 5cm
-
B.
r1 = 5cm, r2 = 10cm
-
C.
r1 = r2 = 10cm
-
D.
r1 = r2 = 5cm
Đáp án : D
+ Áp dụng biểu thức định luật Cu-lông
+ Vận dụng phương pháp tổng hợp lực
+ Vận dụng điều kiện cân bằng của vật
- Gọi lực do q1 tác dụng lên q3 là F1, lực do q2 tác dụng lên q3 là F2
- Để q3 nằm cân bằng: \(\overrightarrow {{F_1}} = - \overrightarrow {{F_2}} \)
- Vì q1 = q2 và cùng dấu nên điểm C phải nằm trong khoảng của AB
=> r1 = r2 = \(\frac{r}{2} = 5\)cm
Hai điện tích \({q_1} = {\rm{ }}2.{\rm{ }}{10^{ - 8}}C\) , \({q_2} = {\rm{ }} - 8.{\rm{ }}{10^{ - 8}}C\) đặt tại A và B trong không khí, \(AB{\rm{ }} = {\rm{ }}8{\rm{ }}cm\). Một điện tích \({q_3}\) đặt tại C. Dấu và độ lớn của \({q_3}\) để \({q_1}\) và \({q_2}\) cũng cân bằng ?
-
A.
\( \pm {4.10^{ - 6}}C\)
-
B.
\( - {8.10^{ - 6}}C\)
-
C.
\({4.10^{ - 8}}C\)
-
D.
\( \pm {8.10^{ - 6}}C\)
Đáp án : B
+ Áp dụng biểu thức định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
+ Vận dụng phương pháp tổng hợp lực
+ Vận dụng điều kiện cân bằng của vật
- Gọi lực do \({q_1}\) tác dụng lên \({q_3}\) là \({F_1}\); lực do \({q_2}\) tác dụng lên \({q_3}\) là \({F_2}\)
- Để \({q_3}\) nằm cân bằng: \(\overrightarrow {{F_1}} = - \overrightarrow {{F_2}} \)
- Vì \({q_1} \ne {q_2}\) và trái dấu nên điểm C phải nằm ngoài khoảng của AB.
- Vì \({q_2} = {\rm{ }}4{q_1}\) (1)
Lại có : \({F_1} = {F_2} \Leftrightarrow k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{r_1^2}} = k\dfrac{{\left| {{q_2}{q_3}} \right|}}{{r_2^2}}\) (2)
Từ (1) và (2) ta suy ra : \( \Rightarrow {r_2} = 2{r_1}\)
Vậy điểm C nằm cách điểm A, B là: \({r_1} = {\text{ }}CA = {\text{ }}8{\text{ }}cm;{r_2} = {\text{ }}CB{\text{ }} = {\text{ }}16{\text{ }}cm\).
Xét các lực tác dụng lên \({q_1}\), ta có : \(\left\{ \begin{array}{l}{F_{31}} = k\dfrac{{\left| {{q_1}{q_3}} \right|}}{{C{A^2}}}\\{F_{21}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{A{B^2}}}\end{array} \right.\)
Ta có, \({q_1}\) cũng cân bằng nên \({F_{31}} = {F_{13}} \Leftrightarrow \dfrac{{\left| {{q_3}} \right|}}{{C{A^2}}} = \dfrac{{\left| {{q_2}} \right|}}{{A{B^2}}}\)
\(\begin{array}{l} \Rightarrow \left| {{q_3}} \right| = \left| {{q_2}} \right|\dfrac{{C{A^2}}}{{A{B^2}}} = {8.10^{ - 8}}\dfrac{{{8^2}}}{{{8^2}}} = {8.10^{ - 8}}\\ \Rightarrow {q_3} = \pm {8.10^{ - 8}}C\end{array}\)
Mặt khác, để tại \(q_1\) và \(q_2\) cũng cân bằng (\(q_1,q_2\) trái dấu, \(q_3\) nằm ngoài \(q_1,q_2\)) nên ta suy ra \(q_3<0\) hay \(q_3=-8.10^{-8}C\)
Tại ba đỉnh của một tam giác đều, người ta đặt ba điện tích giông nhau q1 = q2 = q3 = 6.10-7 C. Cần phải đặt điện tích thứ tư q0 tại đâu, có giá trị bằng bao nhiêu để hệ thống cân bằng.
-
A.
Tâm của tam giác, q0 = - 3,46.107C
-
B.
Tâm của tam giác, q0 = 3,46.10-7C
-
C.
Tâm đường tròn ngoại tiếp, q0 = 3,46.10-7C
-
D.
Tâm đường tròn nội tiếp, q0 = 3,46.10-7C
Đáp án : A
+ Áp dụng điều kiện cân bằng của vật
+ Áp dụng biểu thức định luật Cu-lông
+ Sử dụng phương pháp tổng hợp lực
+ Áp dụng hệ thức trong tam giác
Vì 3 điện tích q1, q2, q3 bằng nhau, nên nếu một điện tích cân bằng thì cả ba điện tích sẽ cân bằng
- Xét lực tác dụng lên q3 là: \(\overrightarrow {{F_3}} = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{23}}} \)
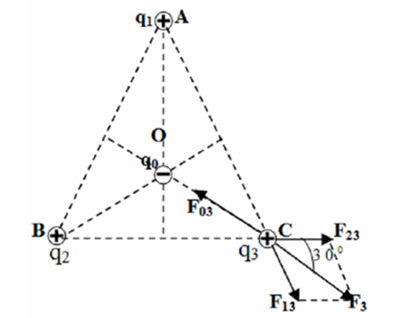
Với \({F_{13}} = {F_{23}} = k\frac{{{q^2}}}{{{a^2}}} \to {F_3} = 2{F_{13}}{\rm{cos3}}{{\rm{0}}^0} = {F_{13}}\sqrt 3 \)
- Lực \(\overrightarrow {{F_3}} \) có phương là phân giác của góc C
=> Để q3 cân bằng thì cần phải có thêm lực \(\overrightarrow {{F_{03}}} \)do q0 tác dụng lên q3 sao cho \(\left\{ \begin{array}{l}\overrightarrow {{F_3}} \uparrow \downarrow \overrightarrow {{F_{03}}} \\{F_3} = {F_{03}}\end{array} \right.\)
$ \to {q_0} < 0$
- Xét tương tự với q1, q2, q3 thì q0 phải nằm tại tâm của tam giác và điện tích ${q_0} < 0$:
Vậy: \({F_{03}} = {F_3} = k\frac{{\left| {{q_0}{q_3}} \right|}}{{{{\left( {\frac{2}{3}\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = k\frac{{\left| {{q_0}q} \right|}}{{{a^2}}}.3 \to {q_0} = - 3,{46.10^{ - 7}}C\)
Bốn điện tích q = 3.10-7C giống nhau đặt tại 4 đỉnh của hình vuông. Phải đặt một điện tích q0 nằm ở đâu và bằng bao nhiêu để năm điện tích này cân bằng
-
A.
Tâm hình hình vuông, q0 = -2,87.10-7C
-
B.
1 đỉnh hình vuông, q0 = 2,87.10-7C
-
C.
Tâm hình vuông, q0 = 2,87.10-7C
-
D.
1 đỉnh hình vuông, q0 = -2,87.10-7C
Đáp án : A
+ Áp dụng điều kiện cân bằng của vật
+ Áp dụng biểu thức định luật Cu-lông
+ Sử dụng phương pháp tổng hợp lực
+ Áp dụng hệ thức trong tam giác
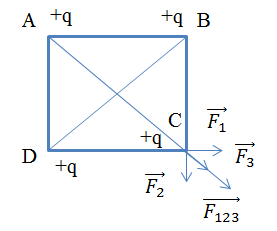
- 3 điện tích tại 3 đỉnh tác dụng vào điện tích q ở C
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {{F_{123}}} \)
Ta có: \(\overrightarrow {{F_{123}}} \) có phương thuộc đường chéo của hình vuông
Để q0 cân bằng: 4 điện tích tương đương với q0 cân bằng với q ở C
\(\overrightarrow {{F_0}} + \overrightarrow {{F_{123}}} = 0 \to \overrightarrow {{F_0}} = - \overrightarrow {{F_{123}}} \)
Tương tự q0 đặt trên đường chéo BD
=> Để năm điện tích cân bằng => q0 là giao điểm của AC và BD.
Muốn \(\overrightarrow {{F_0}} \)trực đối với \(\overrightarrow {{F_{123}}} \)=> q0 < 0
- Mặt khác:
\(\begin{array}{l}{F_0} = {F_{123}}{\rm{ (1)}}\\{F_0} = k\frac{{\left| {q{q_0}} \right|}}{{O{C^2}}} = k\frac{{\left| {q{q_0}} \right|}}{{{{(a\frac{{\sqrt 2 }}{2})}^2}}} = k\frac{{\left| {q{q_0}} \right|}}{{{a^2}}}2{\rm{ (2)}}\\\left\{ \begin{array}{l}{F_1} = {F_2} = k\frac{{{q^2}}}{{{a^2}}}\\{F_{12}} = \sqrt {{F_1}^2 + {F_2}^2} = {F_1}\sqrt 2 = k\frac{{{q^2}}}{{{a^2}}}\sqrt 2 \end{array} \right.\\{F_3} = k\frac{{{q^2}}}{{A{C^2}}} = k\frac{{{q^2}}}{{{{(a\sqrt 2 )}^2}}} = k\frac{{{q^2}}}{{2{{\rm{a}}^2}}}\\{F_{123}} = {F_{12}} + {F_3} = k\frac{{{q^2}}}{{{a^2}}}\sqrt 2 + k\frac{{{q^2}}}{{2{{\rm{a}}^2}}}{\rm{ (3)}}\end{array}\)
Từ (1), (2) và (3) ta có:
\(\begin{array}{l}k\frac{{\left| {q{q_0}} \right|}}{{{a^2}}}2 = k\frac{{{q^2}}}{{{a^2}}}\sqrt 2 + k\frac{{{q^2}}}{{2{{\rm{a}}^2}}}\\ \to \left| {{q_0}} \right| = \frac{q}{2}(\sqrt 2 + \frac{1}{2}) = 2,{87.10^{ - 7}}C\\ \to {q_0} = - 2,{87.10^{ - 7}}C\end{array}\)
Một quả cầu khối lượng \(m = 4g\) treo bằng một sợi chỉ mảnh. Điện tích của quả cầu là \({q_1} = {2.10^{ - 8}}C\). Phía dưới quả cầu dọc theo phương của sợi chỉ có một điện tích \({q_2}\). Khoảng cách giữa hai điện tích là \(r = 5cm\) và lực căng dây là \(T = {5.10^{ - 2}}N\). Xác định điện tích \({q_2}\) và lực tác dụng giữa chúng, lấy \(g = 10m/{s^2}\)
-
A.
\({q_2} = - 1,{39.10^{ - 7}}C\)
-
B.
\({q_2} = 1,{39.10^{ - 7}}C\)
-
C.
\({q_2} = 1,{25.10^{ - 6}}C\)
-
D.
\({q_2} = - 1,{25.10^{ - 6}}C\)
Đáp án : A
+ Vận dụng tương tác giữa các điện tích
+ Sử dụng biểu thức tính lực tương tác giữa 2 điện tích: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Ta có:
+ Trọng lượng \(P = mg = \dfrac{4}{{1000}}.10 = 0,04N\)
Lực căng dây \(T = {5.10^{ - 2}}N\)
Nhận thấy \(T > P \Rightarrow \) lực tương tác giữa hai điện tích phải có chiều như hình vẽ sau:
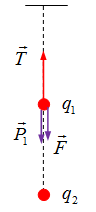
Ta suy ra hai điện tích hút nhau (trái dấu)
Lại có \({q_1} > 0 \Rightarrow {q_2} < 0\)
\(\overrightarrow T + \overrightarrow P + \overrightarrow F = \overrightarrow 0 \)
Chiếu theo phương hướng xuống của sợi dây ta có:
\(\begin{array}{l} - T + P + F = 0\\ \Rightarrow F = T - P = {5.10^{ - 2}} - 0,04 = 0,01N\end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = 0,01N\\ \Rightarrow \left| {{q_2}} \right| = \dfrac{{0,01.0,{{05}^2}}}{{{{9.10}^9}{{.2.10}^{ - 8}}}} = 1,{399.10^{ - 7}}C\end{array}\)
\( \Rightarrow {q_2} = - 1,{39.10^{ - 7}}C\) (do điều kiện \({q_2} < 0\) suy ra ở trên)
Hai quả cầu nhỏ giống hệt nhau bằng kim loại A và B đặt trong không khí, có điện tích lần lượt là q1 = -3,2.10-7 C, q2 = 2,4.10-7 C, cách nhau một khoảng 12 cm. Xác định số electron thừa và thiếu ở mỗi quả cầu?
-
A.
Số electron thiếu ở quả cầu A là 2.1012 electron. Số electron thừa ở quả cầu B là 1,5.1012 electron
-
B.
Số electron thừa ở quả cầu A là 1,5.1012 electron. Số electron thiếu ở quả cầu B là 2.1012 electron
-
C.
Số electron thừa ở quả cầu A là 2.1012 electron. Số electron thiếu ở quả cầu B là 1,5.1012 electron
-
D.
Số electron thiếu ở quả cầu A là 1,5.1012 electron. Số electron thừa ở quả cầu B là 2.1012 electron
Đáp án : C
Công thức tính điện tích: q = n.e
Số electron thừa ở quả cầu A là: \({n_A} = \left| {\frac{{{q_A}}}{e}} \right| = {2.10^{12}}\,\,\left( {electron} \right)\)
Số electron thiếu ở quả cầu B là: \({n_B} = \left| {\frac{{{q_B}}}{e}} \right| = 1,{5.10^{12}}\,\,\left( {electron} \right)\)
Cho hai quả cầu kim loại nhỏ, giống nhau, tích điện và cách nhau 20 cm thì chúng hút nhau một lực bằng 1,2 N. Cho chúng tiếp xúc với nhau rồi tách chúng ra đến khoảng cách như cũ thì chúng đẩy nhau một lực bằng lực hút. Tính điện tích lúc đầu của mỗi quả cầu
-
A.
\({q_1} = 0,{96.10^{ - 6}}C;{q_2} = - 5,{58.10^{ - 6}}C\)
-
B.
\({q_1} = - 5,{58.10^{ - 6}}C;{q_2} = 0,{96.10^{ - 6}}C\)
-
C.
Một kết quả khác
-
D.
A hoặc B
Đáp án : D
Công thức tính lực tương tác: \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
- Hai quả cầu ban đầu hút nhau nên chúng mang điện trái dấu.
- Từ giả thiết bài toán, ta có: \(\left\{ \begin{array}{l}\left| {{q_1}{q_2}} \right| = - {q_1}{q_2} = \frac{{F{r^2}}}{k} = \frac{{16}}{3}{.10^{ - 12}}\\{\left( {\frac{{{q_1} + {q_2}}}{2}} \right)^2} = \frac{{F{r^2}}}{k} \Rightarrow {q_1} + {q_2} = \pm \frac{{\sqrt {192} }}{3}{.10^{ - 6}}\end{array} \right.\)
Theo hệ thức Vi – et thì q1 và q2 là nghiệm của phương trình:
\({q^2} \pm \frac{{\sqrt {192} }}{3}{.10^{ - 6}}q - \frac{{16}}{3}{.10^{ - 12}} = 0 \Rightarrow \left( \begin{array}{l}\left\{ \begin{array}{l}{q_1} = 0,{96.10^{ - 6}}C\\{q_2} = - 5,{58.10^{ - 6}}C\end{array} \right.\\\left\{ \begin{array}{l}{q_1} = - 5,{58.10^{ - 6}}C\\{q_2} = 0,{96.10^{ - 6}}C\end{array} \right.\end{array} \right.\)
Cho hai loại điện tích q1và q2 đặt cách nhau 15cm trong không khí, lực tác dụng giữa chúng là F. Khi đặt chúng trong dầu thì lực này còn bằng F/2,25. Để lực tác dụng vẫn là F thì cần phải dịch chuyển chúng lại một đoạn là
-
A.
5cm
-
B.
10cm
-
C.
6cm
-
D.
8cm
Đáp án : A
Phương pháp :
Công thức Cu – lông : \(F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon .{r^2}}}\)
Cách giải :
Ta có :
\(\left\{ \begin{array}{l}F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{0,{{15}^2}}}\\{F_d} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{\varepsilon _d}.0,{{15}^2}}} = \frac{F}{{2,25}}\end{array} \right. \Rightarrow {\varepsilon _d} = 2,25\)
Để lực tác dụng vẫn là F :
\(\left\{ \begin{array}{l}F = \frac{{k\left| {{q_1}{q_2}} \right|}}{{0,{{15}^2}}}\\{F_d} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{{\varepsilon _d}.r{'^2}}} = F\end{array} \right. \Rightarrow \frac{{k\left| {{q_1}{q_2}} \right|}}{{2,25.r{'^2}}} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{0,{{15}^2}}} \Leftrightarrow \frac{1}{{2,25.r{'^2}}} = \frac{1}{{0,{{15}^2}}} \Rightarrow r' = 10cm = r - 5cm\)
Cho 4 điện tích \({q_{1\;}} = {q_{3\;}} = {4.10^{ - 6}}C;{q_{2\;}} = {q_4} = - {4.10^{ - 6}}C\) giống nhau đặt tại 4 đỉnh của hình vuông ABCD cạnh 10cm theo thứ tự A, B, C, D. Tìm lực điện tác dụng lên \({q_0} = - {2.10^{ - 6}}C\) đặt tại tâm O của hình vuông.
-
A.
\(4,{2.10^{ - 4}}N\)
-
B.
\(2,{1.10^{ - 4}}N\)
-
C.
\(8,{4.10^{ - 4}}N\)
-
D.
\(0N\)
Đáp án : D
+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.
+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \)
+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.
Biểu diễn các lực tác dụng lên q0 như hình vẽ:
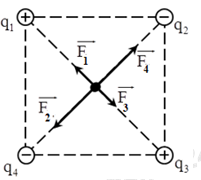
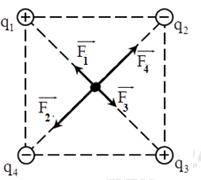
Lực tổng hợp tác dụng lên q0: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} \)
Lực tương tác giữa hai điện tích được xác định bởi công thức: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right|\\OA = OB = OC = OD\end{array} \right. \Rightarrow {F_1} = {F_2} = {F_3} = {F_4}\)
Mặt khác: \(\left\{ \begin{array}{l}\overrightarrow {{F_1}} \uparrow \downarrow \overrightarrow {{F_3}} \Rightarrow {F_{13}} = \left| {{F_1} - {F_3}} \right| = 0\\\overrightarrow {{F_2}} \uparrow \downarrow \overrightarrow {{F_4}} \Rightarrow {F_{24}} = \left| {{F_2} - {F_4}} \right| = 0\end{array} \right. \Rightarrow \overrightarrow F = \overrightarrow {{F_{13}}} + \overrightarrow {{F_{24}}} = 0\)
Cho 4 điện tích \({q_{1\;}} = {q_{2\;}} = {q_{3\;}} = {q_4} = - {2.10^{ - 8}}C\) lần lượt đặt tại 4 đỉnh của hình vuông ABCD cạnh 4cm theo thứ tự A, B, C, D. Tìm lực điện tổng hợp tác dụng lên điện tích đặt tại D?
-
A.
\(2,{31.10^{ - 3}}N\)
-
B.
\(2,{06.10^{ - 3}}N\)
-
C.
\(4,{06.10^{ - 3}}N\)
-
D.
\(4,{31.10^{ - 3}}N\)
Đáp án : D
+ Lực tương tác giữa hai điện tích: \({F_{12}} = \dfrac{{k.\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
+ Hai điện tích cùng dấu thì đẩy nhau, hai điện tích trái dấu thì hút nhau.
+ Lực tổng hợp tác dụng lên điện tích điểm: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \)
+ Vẽ hình, sử dụng các kiến thức hình học để tính toán.
Biểu diễn các lực tác dụng lên q4 như hình vẽ:
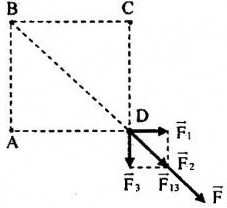
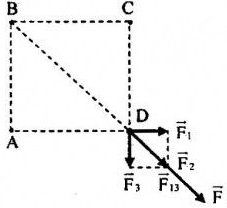
Ta có: \(\left\{ \begin{array}{l}\left| {{q_{1\;}}} \right| = \left| {{q_{2\;}}} \right| = \left| {{q_{3\;}}} \right| = \left| {{q_4}} \right| = {2.10^{ - 8}}C\\AB = BC = CD = DA = 4cm\\BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 cm\end{array} \right. \Rightarrow {F_1} = {F_3}\)
Lực tác dụng lên q4: \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \)
Với: \(\left\{ \begin{array}{l}{F_1} = {F_3} = \dfrac{{k.\left| {{q_1}{q_4}} \right|}}{{A{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {{{4.10}^{ - 2}}} \right)}^2}}} = 2,{25.10^{ - 3}}N\\{F_2} = \dfrac{{k.\left| {{q_2}{q_4}} \right|}}{{B{D^2}}} = \dfrac{{{{9.10}^9}.{{\left( {{{2.10}^{ - 8}}} \right)}^2}}}{{{{\left( {4\sqrt 2 {{.10}^{ - 2}}} \right)}^2}}} = 1,{125.10^{ - 3}}N\end{array} \right.\)
Ta có: \(\overrightarrow {{F_{13}}} = \overrightarrow {{F_1}} + \overrightarrow {{F_3}} \)
Vì \(\overrightarrow {{F_1}} \bot \overrightarrow {{F_3}} \Rightarrow {F_{13}} = \sqrt {F_1^2 + F_3^2} = {F_1}\sqrt 2 = 2,25\sqrt 2 {.10^{ - 3}}N\)
Ta có: \(\overrightarrow F = \overrightarrow {{F_2}} + \overrightarrow {{F_{13}}} \)
Mà \(\overrightarrow {{F_2}} \uparrow \uparrow \overrightarrow {{F_{13}}} \Rightarrow F = {F_2} + {F_{23}} = 4,{31.10^{ - 3}}N\)
Người ta treo hai quả cầu nhỏ khối lượng bằng nhau m = 0,1g bằng hai sợi dây nhę có độ dài l = 1,5m như nhau. Cho chúng nhiễm điện bằng nhau thì chúng đẩy nhau và cân bằng khi mỗi dây treo hợp với phương thẳng đứng một góc \({15^0}\). Tính độ lớn điện tích tích cho mỗi quả cầu. Lấy \(g = 10m/{s^2}\)
-
A.
\(178,{63.10^{ - 9}}{\rm{C}}\)
-
B.
\(103,{5.10^{ - 5}}{\rm{C}}\)
-
C.
\(89,{32.10^{ - 9}}{\rm{C}}\)
-
D.
\(133,{97.10^{ - 9}}{\rm{C}}\)
Đáp án : D
Phân tích các lực tác dụng vào quả cầu.
Áp dụng công thức: \(\tan \alpha {\rm{ \;}} = \frac{{{F_d}}}{P} \Rightarrow {F_d}\)
Mà lực điện tương tác giữa 2 quả cầu: \(F = \frac{{k{q^2}}}{{{r^2}}}\)
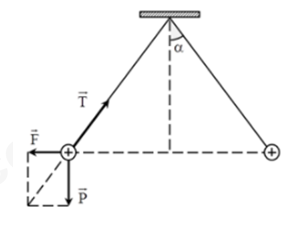
Đổi \({15^0} = \frac{\pi }{{12}}{\mkern 1mu} {\mkern 1mu} \left( {rad} \right)\)
Các lực tác dụng vào quả cầu khi điện tích cân bằng:
\(\vec P{\rm{ \;}} + \overrightarrow {{F_d}} {\rm{ \;}} + \vec T{\rm{ \;}} = \vec 0\)
\(\tan \alpha {\rm{ \;}} = \frac{F}{P} = \frac{{\frac{{k.{q^2}}}{{{r^2}}}}}{{mg}} \Rightarrow {q^2} = \frac{{{r^2}mg\tan \alpha }}{k}\)
Ta có: \(\sin \alpha {\rm{ \;}} = \frac{r}{{2l}} \Rightarrow r = 2l.\sin \alpha {\rm{ \;}} = 2.1,5.\sin {15^0} \approx 0,7765\left( m \right)\)
Do vậy độ lớn của điện tích đã tích cho qua cầu là:
\(\begin{array}{*{20}{l}}{\left| q \right| = \sqrt {\frac{{{r^2}mg.\tan \alpha }}{k}} {\rm{ \;}} = \sqrt {\frac{{0,{{7765}^2}.0,{{1.10}^{ - 3}}.10.\tan {{15}^0}}}{{{{9.10}^9}}}} }\\{ \Rightarrow \left| q \right| \approx 1,{{3397.10}^{ - 7}}{\mkern 1mu} \left( C \right) = 133,{{97.10}^{ - 9}}\left( C \right)}\end{array}\)
Hai điện tích điểm bằng nhau đặt trong không khí cách nhau 12cm, lực tương tác giữa chúng bằng 40N. Các điện tích đó bằng:
-
A.
\( \pm 12\mu {\rm{C}}\)
-
B.
\( \pm 8\mu {\rm{C}}\)
-
C.
\( \pm 4\mu {\rm{C}}\)
-
D.
\( \pm 5\mu {\rm{C}}\)
Đáp án : B
Áp dụng công thức: \(F = \frac{{k{q^2}}}{{{r^2}}}\)
Ta có: \(F = \frac{{k{q^2}}}{{{r^2}}}\) \( \Rightarrow q = {\rm{ \;}} \pm \sqrt {\frac{{F.{r^2}}}{k}} {\rm{ \;}} = {\rm{ \;}} \pm \sqrt {\frac{{40.{{\left( {{{12.10}^{ - 2}}} \right)}^2}}}{{{{9.10}^9}}}} {\rm{ \;}} = {\rm{ \;}} \pm {8.10^{ - 6}}\left( C \right) = {\rm{ \;}} \pm 8\mu C\)
Luyện tập và củng cố kiến thức Bài 3. Điện trường Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3. Bài tập điện trường Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4. Công của lực điện - Hiệu điện thế Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập công của lực điện - Hiệu điện thế Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6. Tụ điện Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập về tụ điện Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập chuyển động của điện tích trong điện trường Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập chương 1 Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập định luật Culông (phần 1) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2. Thuyết electron và định luật bảo toàn điện tích Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1. Điện tích - Định luật Culông Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết










Danh sách bình luận