-
Chương 1. Điện tích. Điện trường
- Bài 1. Điện tích - Định luật Culông
- Bài 2. Thuyết electron và định luật bảo toàn điện tích
- Tổng hợp bài tập định luật Culông (phần 1)
- Tổng hợp bài tập định luật Culông (phần 2)
- Bài 3. Điện trường
- Bài 3. Bài tập điện trường
- Bài 4. Công của lực điện - Hiệu điện thế
- Tổng hợp bài tập công của lực điện - Hiệu điện thế
- Bài 6. Tụ điện
- Tổng hợp bài tập về tụ điện
- Tổng hợp bài tập chuyển động của điện tích trong điện trường
- Ôn tập chương 1
-
Chương 2. Dòng điện không đổi
- Bài 7. Đại cương về dòng điện không đổi - Nguồn điện
- Bài 8. Điện năng và công suất điện
- Tổng hợp bài tập tính điện trở dây dẫn, biến trở
- Bài 9. Định luật Ôm cho đoạn mạch chỉ có điện trở
- Bài 9. Định luật Ôm đối với toàn mạch - Mắc nguồn điện thành bộ
- Tổng hợp bài tập định luật Ôm
- Bài 9. Định luật Ôm cho mạch chứa tụ điện
- Ôn tập chương 2
-
Chương 3. Dòng điện trong các môi trường
-
Chương 4. Từ trường
- Bài 19. Từ trường
- Bài 20. Lực từ - Cảm ứng từ
- Bài 21. Từ trường của dòng điện trong các dây dẫn có hình dạng đặc biệt
- Bài 21. Tương tác giữa hai dòng điện song song
- Bài 21. Khung dây đặt trong từ trường đều
- Bài 22. Lực Lorenxơ
- Bài 22. Chuyển động của hạt mang điện trong từ trường đều
- Ôn tập chương 4
-
Chương 5. Cảm ứng điện từ
-
Chương 6. Khúc xạ ánh sáng
-
Chương 7. Mắt. Các dụng cụ quang
Trắc nghiệm Bài 3. Bài tập điện trường - Vật Lí 11
Đề bài
Xác định cường độ điện trường tại điểm M trong không khí cách điện tích điểm q = 2.10-8 C một khoảng 3 cm.
-
A.
2.104 V/m
-
B.
20 V/m
-
C.
2.105 V/m
-
D.
4.10-3 V.m
Một điện tích điểm dương Q trong chân không gây ra một điện trường có cường độ E = 3.104 V/m tại điểm M cách điện tích một khoảng 30 cm. Tính độ lớn điện tích Q ?
-
A.
3mC
-
B.
0,3μC
-
C.
0,3nC
-
D.
3μC
Một điện tích điểm q = 10-7 C đặt tại điểm M trong điện trường của một điện tích điểm Q, chịu tác dụng của một lực F = 3.10-3 N. Cường độ điện trường do điện tích điểm Q gây ra tại M có độ lớn là bao nhiêu?
-
A.
$3.10^4V/cm$
-
B.
$3.10^5V/m$
-
C.
$3.10^2 V/cm$
-
D.
$3.10^3 V/m$
Cường độ điện trường tạo bởi một điện tích điểm cách nó 2 cm bằng 105 V/m. Tại vị trí cách điện tích này bằng bao nhiêu thì cường độ điện trường bằng 4.105 V/m?
-
A.
2 cm.
-
B.
1 cm.
-
C.
4 cm.
-
D.
5 cm.
Cường độ điện trường do điện tích +Q gây ra tại điểm A cách nó một khoảng r có độ lớn là E. Nếu thay bằng điện tích -2Q và giảm khoảng cách đến A còn một nửa thì cường độ điện trường tại A có độ lớn là
-
A.
\(8E\)
-
B.
\(4E\)
-
C.
\(0,25E\)
-
D.
\(E\)
Một điện tích điểm Q = - 2.10-7 C, đặt tại điểm A trong môi trường có hằng số điện môi \(\varepsilon = 2\). Véc tơ cường độ điện trường \(\overrightarrow E \) do điện tích Q gây ra tại điểm B với AB = 6 cm có
-
A.
phương AB, chiều từ A đến B, độ lớn \(2,{5.10^5}V/m\)
-
B.
phương AB, chiều từ B đến A, độ lớn \(1,{5.10^4}V/m\)
-
C.
phương AB, chiều từ B đến A, độ lớn \(2,{5.10^5}V/m\)
-
D.
phương AB, chiều từ A đến B, độ lớn \(2,{5.10^4}V/m\)
Cho \({q_1} = {\rm{ }}{4.10^{ - 10}}C,{\rm{ }}{q_2} = {\rm{ }} - 4.{\rm{ }}{10^{ - 10}}C\), đặt tại $A$ và $B$ trong không khí biết $AB = 2 cm$. Xác định vectơ \(\vec E\) tại điểm $H$ - là trung điểm của $AB$.
-
A.
\({72.10^3}V/m\)
-
B.
\({36.10^3}V/m\)
-
C.
\(0{\rm{ }}V/m\)
-
D.
\({36.10^5}V/m\)
Cho ${q_1} = {\rm{ }}{4.10^{ - 10}}C,{\rm{ }}{q_2} = {\rm{ }} - 4.{\rm{ }}{10^{ - 10}}C$, đặt tại A và B trong ko khí biết $AB{\rm{ }} = {\rm{ }}2{\rm{ }}cm$. Xác định vectơ $\vec E$tại điểm $M$, biết $MA{\rm{ }} = {\rm{ }}1{\rm{ }}cm,{\rm{ }}MB{\rm{ }} = {\rm{ }}3{\rm{ }}cm$.
-
A.
${72.10^3}V/m$
-
B.
${32.10^3}V/m$
-
C.
$0{\rm{ }}V/m$
-
D.
${40.10^3}V/m$
Cho q1 = 4.10-10 C, q2 = -4. 10-10 C, đặt tại A và B trong ko khí biết AB = 2 cm. Xác định vectơ \(\vec E\) tại điểm N, biết rằng NAB là một tam giác đều.
-
A.
32.103 V/m
-
B.
2.103 V/m
-
C.
9.103 V/m
-
D.
3.103 V/m
Hai điện tích q1 = 8. 10-8 C, q2 = -8. 10-8 C đặt tại A và B trong không khí biết AB = 4 cm. Tìm vectơ cường độ điện trường tại C trên đường trung trực của AB và cách AB 2 cm?
-
A.
18.105 V/m
-
B.
9.105 V/m
-
C.
12,73.105 V/m
-
D.
0 V/m
Tại ba đỉnh của tam giác ABC vuông tại A, AB = 30cm, AC = 40cm và BC = 50cm. Đặt các điện tích q1 = q2 = q3 = 10-9 C. Xác định độ lớn cường độ điện trường tại điểm H- là chân đường cao kẻ từ A.
-
A.
156,25 V/m
-
B.
246 V/m
-
C.
259 V/m
-
D.
290 V/m
Bốn điểm A, B, C, D trong không khí tạo thành hình chữ nhật ABCD cạnh AD = 3cm; AB = 4cm. Các điện tích q1, q2, q3 đặt lần lượt tại A, B, C. Gọi \(\overrightarrow {{E_2}} \) là véctơ cường độ điện trường do điện tích q2 gây ra tại D. \(\overrightarrow {{E_{13}}} \)là cường độ điện trường tổng hợp do các điện tích q1 và q3 gây ra tại D. Xác định giá trị của q1 và q3 biết q2 = -12,5.10-8C và \(\overrightarrow {{E_{13}}} = \overrightarrow {{E_2}} \)
-
A.
q1 = -2,7.10-8C, q3 = -6,4.10-8C
-
B.
q1 = 2,7.10-8C, q3 = 6,4.10-8C
-
C.
q1 = -6,4.10-8C , q3 = -2,7.10-8C
-
D.
q1 = 6,4.10-8C , q3 = -2,7.10-8C
Cho hai điện tích q1 = 1nC, q2 = -8nC đặt tại hai điểm A, B cách nhau 30cm trong chân không. Tìm điểm C cách A và B bao nhiều sao cho tại đó\(\overrightarrow {{E_2}} = 2\overrightarrow {{E_1}} \)
-
A.
CA = 20cm, CB = 20cm
-
B.
CA = 20cm, CB = 10cm
-
C.
CA = 15cm, CB = 15cm
-
D.
CA = 10cm, CB = 20cm
Hai điện tích điểm q1 = 4.10-6C; q2 = 36.10-6C đặt tại hai điểm cố đinh A và B trong dầu có hằng số điện môi ε = 2. AB = 16cm. Xác định vị trí của điểm M mà tại đó cường độ điện trường tổng hợp bằng không?
-
A.
MA = 4cm, MB = 12cm
-
B.
MA = 12cm, MB = 4cm
-
C.
MA = 8cm, MB = 8cm
-
D.
MA = 4cm, MB = 20cm
Cho hình vuông ABCD cạnh a, tại A và C đặt các điện tích q1 = q3 = q > 0. Cần đặt ở B điện tích bằng bao nhiêu để cường độ điện trường ở D bằng 0.
-
A.
\( - 2\sqrt 2 q\)
-
B.
\(2\sqrt 2 q\)
-
C.
\( - 2q\)
-
D.
\(2q\)
Một quả cầu nhỏ mang điện tích được cân bằng trong điện trường do tác dụng của trọng lực và lực điện trường. Đột ngột giảm độ lớn điện trường đi còn một nửa nhưng vẫn giữ nguyên phương và chiều của đường sức điện. Thời gian để quả cầu di chuyển được 5cm trong điện trường. Lấy g = 10m/s2
-
A.
0,1s
-
B.
0,071s
-
C.
0,173s
-
D.
0,141s
Cho hai tấm kim loại song song, nằm ngang, nhiễm điện trái dấu. Khoảng không gian giữa hai tấm kim loại chứa đầy dầu. Điện trường giữa hai tấm kim loại là điện trường đều hướng từ trên xuống và có độ lớn 20000V/m. Một quả cầu bằng sắt có bán kính 1cm mang điện tích q nằm lơ lửng ở khoảng không gian giữa hai tấm kim loại. Điện tích q có giá trị bằng bao nhiểu? Biết khối lượng riêng của sắt là 7800kg/m3, của dầu là 800kg/m3. Lấy g = 10m/s2.
-
A.
q = -4.10-6C
-
B.
q = 4.10-6C
-
C.
q = -14,7.10-6C
-
D.
q = 14,7.10-6C
Một con lắc đơn gồm một quả cầu tích điện dương khối lượng \(\sqrt 3 g\) buộc vào sợi dây mảnh cách điện. Con lắc treo trong điện trường đều có phương nằm ngang với cường độ điện trường 10000 V/m. Tại nơi có g = 9,8m/s2. Khi vật ở vị trí cân bằng, sợi dây lệch một góc α = 300 so với phương thẳng đứng. Độ lớn của điện tích của quả cầu là?
-
A.
4.10-7C
-
B.
3,27.10-7C
-
C.
9,8.10-7C
-
D.
10-7C
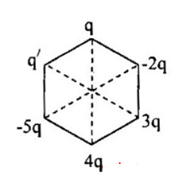
Đặt tại $6$ đỉnh của lục giác đều các điện tích $q$, $-2q$, $3q$, $4q$, $-5q$ và $q'$. Xác định $q'$ theo $q$ để cường độ điện trường tại tâm O của lục giác bằng $0$ biết $q > 0$.
-
A.
$q'= -6q$
-
B.
$q'= 6q$
-
C.
$q'=-q$
-
D.
$q'= q$
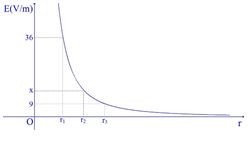
Cường độ điện trường của một điện tích phụ thuộc vào khoảng cách r được mô tả như đồ thị bên. Biết \({r_2} = \dfrac{{{r_1} + {r_3}}}{2}\)và các điểm cùng nằm trên một đường sức. Giá trị của x bằng
-
A.
\(13,5 V/m\)
-
B.
\(17 V/m\)
-
C.
\(22,5 V/m\)
-
D.
\(16 V/m\)
Hai điện tích điểm \({q_1} = - 9\mu C,{\rm{ }}{q_2} = 4\mu C\) đặt lần lượt tại A,B có thể tìm thấy vị trí của điểm M mà tại đó điện trường tổng hợp bằng không trên
-
A.
Đường trung trực của AB
-
B.
Đường thẳng AB, nằm ngoài đoạn thằng AB về phía A
-
C.
Đường thẳng AB, nằm ngoài đoạn thẳng AB về phía B
-
D.
Đoạn thẳng AB, vị trí bất kỳ
Đặt 4 điện tích âm có cùng độ lớn \(q\) tại 4 đỉnh của một hình vuông ABCD cạnh \(a.\) Xác định cường độ tổng hợp tại giao điểm hai đường chéo của hình vuông.
-
A.
\({E_O} = 2.\dfrac{{k\left| q \right|}}{{{a^2}}}\)
-
B.
\(0\)
-
C.
\({E_O} = 4.\dfrac{{k\left| q \right|}}{{{a^2}}}\)
-
D.
\({E_O} = \dfrac{2}{{\sqrt 3 }}.\dfrac{{k\left| q \right|}}{{{a^2}}}\)
Tại hai điểm A và B cách nhau \(10cm\) trong không khí có đặt hai điện tích \(q_1 = q_2 = 16.10^{ - 8}C.\) Xác định cường độ điện trường do hai điện tích điểm này gây ra tại C biết \(AC = BC = 8cm.\)
-
A.
\(3,{51.10^5}(V/m)\)
-
B.
\(5,{25.10^5}(V/m)\)
-
C.
\(2,{5.10^5}(V/m)\)
-
D.
\(3,{2.10^5}(V/m)\)
Cho hai điện tích điểm \({q_1} = {6.10^{ - 7}}C;{q_2} = - {8.10^{ - 7}}C\) đặt tại hai điểm A và B trong không khí cách nhau \(5cm.\) Xác định véc tơ cường độ điện trường tổng hợp tại M do \({q_1}\) và \({q_2}\) gây ra tại M biết \(MA = 3cm, MB = 8cm.\)
-
A.
\(71,{25.10^5}V/m\)
-
B.
\(48,{75.10^5}V/m\)
-
C.
\(61,{05.10^5}V/m\)
-
D.
\(35,{63.10^5}V/m\)
Một quả cầu kim loại nhỏ có khối lượng 1g được tích điện q = 10-5C treo vào đầu một sợi dây mảnh và đặt trong điện trường đều E. Khi quả cầu đứng cân bằng thì dây treo hợp với phương thẳng một góc 600, lấy g = 10m/s2. Tìm E.
-
A.
1520V/m
-
B.
1732V/m
-
C.
1341 V/m
-
D.
1124 V/m
Cho hình vuông ABCD, tại A và C đặt các điện tích \(q_1 = q_3 = q = 2,5.10^{ - 8}C.\) Hỏi phải đặt tại B một điện tích bao nhiêu để cường độ điện trường tại D bằng \(0.\)
-
A.
\( - 5\sqrt 2 {.10^{ - 8}}C\)
-
B.
\(5\sqrt 2 {.10^{ - 8}}C\)
-
C.
\({5.10^{ - 8}}C\)
-
D.
\( - {5.10^{ - 8}}C\)
Bốn điểm A, B, C, D trong không khí tạo thành hình chữ nhật ABCD cạnh \(AD = a = 3cm;AB = b = 4cm\). Các điện tích \(q_1\,;\,q_2\,;\,q_3\)được đặt lần lượt tại A, B, C. Biết \(q_2 = - 12,5.10^{ - 8}C\) và cường độ điện trường tổng hợp tại D bằng \(0.\) Tính \({q_1};{q_2}\)?
-
A.
\({q_1} = - 6,{4.10^{ - 8}}C;{q_3} = 2,{7.10^{ - 8}}C\)
-
B.
\({q_1} = 2,{7.10^{ - 8}}C;{q_3} = - 6,{4.10^{ - 8}}C\)
-
C.
\({q_1} = 6,{4.10^{ - 8}}C;{q_3} = 2,{7.10^{ - 8}}C\)
-
D.
\({q_1} = 2,{7.10^{ - 8}}C;{q_3} = 6,{4.10^{ - 8}}C\)
Một quả cầu khối lượng \(m = 4,{5.10^{ - 3}}kg\) treo vào một sợi dây dài \(2m.\) Quả cầu nằm trong điện trường có \(\overrightarrow E \) nằm ngang, hướng sang trái như hình vẽ. Biết \(d = 1m,E = 2000V/m\). Lấy \(g = 10{\rm{ }}m/{s^2}\).
Tính độ lớn của lực căng dây.
-
A.
\(0,09N\)
-
B.
\(0,052N\)
-
C.
\(0,045N\)
-
D.
\(0,156N\)
Một điện tích điểm \({q_1} = {4.10^{ - 6}}C\) đặt tại điểm A trong không khí.
Xác định độ lớn cường độ điện trường do q1 gây ra tại C cách A 10cm.
-
A.
\({3,6.10^5}V/m\)
-
B.
\({36.10^5}V/m\)
-
C.
\({18.10^5}V/m\)
-
D.
\({36.10^4}V/m\)
Tại điểm B đặt thêm \({q_2} = - {16.10^{ - 6}}C\). Biết AB = 40 cm; BC = 30 cm. Xác định cường độ điện trường tổng hợp do q1 và q2 gây ra tại điểm C.
-
A.
\({52.10^5}V/m\)
-
B.
\({20.10^5}V/m\)
-
C.
\({52.10^4}V/m\)
-
D.
\({20.10^4}V/m\)
Tại một điểm trong không khí có hai cường độ điện trường có phương vuông góc với nhau và có độ lớn lần lượt là E1 = 6.104 V/m; E2 = 8.104 V/m. Độ lớn của điện trường tổng là:
-
A.
10.104 V/m
-
B.
14.104 V/m
-
C.
2. 104 V/m
-
D.
48.104 V/m
Một quả cầu nhỏ m = 0,25g, mang điện tích q = 5.10-9 C treo trên sợi dây mảnh trong điện trường đều có phương nằm ngang, cường độ điện trường E = 106V/m cho g = 10m/s2. Độ lớn lực điện trường tác dụng lên quả cầu là
-
A.
7,5.10-5 N
-
B.
3.10-3 N
-
C.
5.10-3 N
-
D.
2,5.10-3 N
Một điện tích \(Q = 1,{6.10^{ - 8}}C\) gây ra một điện trường tại \(A\) có cường độ là \({9.10^4}\) V/m (\(Q\) và \(A\) đều đặt trong chân không). Điểm \(A\) cách \(Q\) một đoạn là
-
A.
1,6 cm
-
B.
16 cm
-
C.
4 cm
-
D.
40 cm
Hai điện tích điểm \({q_1} = {2.10^{ - 8}}C\) và \({q_2} = - {2.10^{ - 8}}C\) đặt tại hai điểm \(A\) và \(B\) cách nhau 30 cm trong không khí. Tại điểm C, cường độ điện trường tổng hợp do \({q_1}\) và \({q_2}\) gây ra bằng 2000 V/m. Chọn câu đúng về vị trí của điểm C.
-
A.
C thẳng hàng với A, B theo thứ tự A, B, C
-
B.
A, B, C tạo thành một tam giác đều
-
C.
C là trung điểm của đoạn AB
-
D.
C thẳng hàng với A, B theo thứ tự C, A, B
Một điện tích \( - 1{\mkern 1mu} \mu C\) đặt trong chân không sinh ra điện trường tại một điểm cách nó 1m có độ lớn và hướng là
-
A.
9000 V/m, hướng ra xa nó.
-
B.
\({9.10^9}\) V/m, hướng về phía nó.
-
C.
\({9.10^9}\) V/m, hướng ra xa nó.
-
D.
9000 V/m, hướng về phía nó.
Một điện tích \(1\mu {\rm{C}}\) đặt trong chân không sinh ra điện trường tại một điểm cách nó 1m có độ lớn và hướng là
-
A.
9000V/m, hướng về phía nó.
-
B.
9000V/m, hướng ra xa nó.
-
C.
\({9.10^9}V/m\), hướng về phía nó.
-
D.
\({9.10^9}V/m\), hướng ra xa nó.
Hai tấm kim loại song song, cách nhau 1cm và được nhiễm điện trái dấu nhau. Muốn làm cho điện tích \({\rm{q}} = {5.10^{ - 10}}C\) di chuyển từ tấm này đến tấm kia cần tốn một công \(A = {2.10^{ - 9}}J\). Coi điện trường bên trong khoảng giữa hai tấm kim loại là điện trường đều và có các đường sức điện vuông góc với các tấm. Cường độ điện trường bên trong tấm kim loại đó là
-
A.
E = 40V/m.
-
B.
E = 200V/m.
-
C.
E = 400V/m.
-
D.
E = 2V/m.
Lời giải và đáp án
Xác định cường độ điện trường tại điểm M trong không khí cách điện tích điểm q = 2.10-8 C một khoảng 3 cm.
-
A.
2.104 V/m
-
B.
20 V/m
-
C.
2.105 V/m
-
D.
4.10-3 V.m
Đáp án : C
Áp dụng công thức xác định cường độ điện trường:
\(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Ta có, cường độ điện trường:
\(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}} = {9.10^9}\frac{{{{2.10}^{ - 8}}}}{{1.{{\left( {0,03} \right)}^2}}} = {2.10^5}V/m\)
=> E = 2.105 V/m.
Một điện tích điểm dương Q trong chân không gây ra một điện trường có cường độ E = 3.104 V/m tại điểm M cách điện tích một khoảng 30 cm. Tính độ lớn điện tích Q ?
-
A.
3mC
-
B.
0,3μC
-
C.
0,3nC
-
D.
3μC
Đáp án : B
Áp dụng biểu thức xác định cường độ điện trường:
\(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Ta có, cường độ điện trường:
\(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}} \to \left| Q \right| = \dfrac{{{\rm{E}}{\rm{.}}{{\rm{r}}^{\rm{2}}}.\varepsilon }}{k} = \dfrac{{{\rm{3}}{\rm{.1}}{{\rm{0}}^4}{\rm{.0,}}{{\rm{3}}^{\rm{2}}}.1}}{{{{9.10}^9}}} = {3.10^{ - 7}}C\)
Một điện tích điểm q = 10-7 C đặt tại điểm M trong điện trường của một điện tích điểm Q, chịu tác dụng của một lực F = 3.10-3 N. Cường độ điện trường do điện tích điểm Q gây ra tại M có độ lớn là bao nhiêu?
-
A.
$3.10^4V/cm$
-
B.
$3.10^5V/m$
-
C.
$3.10^2 V/cm$
-
D.
$3.10^3 V/m$
Đáp án : C
Áp dụng biểu thức: \(E = \dfrac{F}{{\left| q \right|}}\)
Ta có, cường độ điện trường E:
\(E = \dfrac{F}{{\left| q \right|}} = \dfrac{{{{3.10}^{ - 3}}}}{{{{10}^{ - 7}}}} = {3.10^4}V/m = {3.10^2}V/cm\)
Cường độ điện trường tạo bởi một điện tích điểm cách nó 2 cm bằng 105 V/m. Tại vị trí cách điện tích này bằng bao nhiêu thì cường độ điện trường bằng 4.105 V/m?
-
A.
2 cm.
-
B.
1 cm.
-
C.
4 cm.
-
D.
5 cm.
Đáp án : B
Áp dụng biểu thức xác định cường độ điện trường E:
\(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Ta có, cường độ điện trường E:
\(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
+ Tại vị trí cách cách điện tích điểm Q 1 khoảng \(r = 2cm = 0,02m\) thì:
\({E_1} = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}} = {10^5}V/m\)
+ Gọi vị trí cách điện tích để cường độ điện trường E2 = 4.105 V/m là r’
Ta có:
\({E_2} = k\dfrac{{\left| Q \right|}}{{\varepsilon .r{'^2}}} = {4.10^5}V/m\)
\( \to \dfrac{{{E_1}}}{{{E_2}}} = \dfrac{{k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}}}{{k\dfrac{{\left| Q \right|}}{{\varepsilon .r{'^2}}}}} \\= \dfrac{{r{'^2}}}{{{r^2}}} = \dfrac{{{{10}^5}}}{{{{4.10}^5}}} \\\to r' = r\sqrt {\dfrac{{{{10}^5}}}{{{{4.10}^5}}}} = 0,02.\sqrt {\dfrac{{{{10}^5}}}{{{{4.10}^5}}}} \\= 0,01m = 1cm\)
Cường độ điện trường do điện tích +Q gây ra tại điểm A cách nó một khoảng r có độ lớn là E. Nếu thay bằng điện tích -2Q và giảm khoảng cách đến A còn một nửa thì cường độ điện trường tại A có độ lớn là
-
A.
\(8E\)
-
B.
\(4E\)
-
C.
\(0,25E\)
-
D.
\(E\)
Đáp án : A
Áp dụng biểu thức xác định cường độ điện trường E:
\(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Ta có:
+ Ban đầu:
\(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
+ Khi thay bằng điện tích -2Q, r’ = r/2, ta có:
\(E' = k\dfrac{{\left| { - 2Q} \right|}}{{\varepsilon .r{'^2}}} = k\dfrac{{\left| { - 2Q} \right|}}{{\varepsilon .{{\left( {\dfrac{r}{2}} \right)}^2}}} = k\dfrac{{2.4\left| Q \right|}}{{\varepsilon .{r^2}}} = 8E\)
Một điện tích điểm Q = - 2.10-7 C, đặt tại điểm A trong môi trường có hằng số điện môi \(\varepsilon = 2\). Véc tơ cường độ điện trường \(\overrightarrow E \) do điện tích Q gây ra tại điểm B với AB = 6 cm có
-
A.
phương AB, chiều từ A đến B, độ lớn \(2,{5.10^5}V/m\)
-
B.
phương AB, chiều từ B đến A, độ lớn \(1,{5.10^4}V/m\)
-
C.
phương AB, chiều từ B đến A, độ lớn \(2,{5.10^5}V/m\)
-
D.
phương AB, chiều từ A đến B, độ lớn \(2,{5.10^4}V/m\)
Đáp án : C
+ Vận dụng phương pháp xác định phương, chiều của cường độ điện trường
+ Áp dụng biểu thức xác định cường độ điện trường E: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Ta có:
+ Phương : đường thẳng nối điện tích với điểm khảo sát
+ Q < 0 => \(\overrightarrow E \) hướng về phía Q
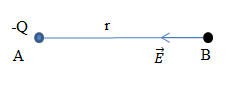
=> E có chiều từ B đến A
+ Độ lớn: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}} = {9.10^9}\dfrac{{\left| { - {{2.10}^{ - 7}}} \right|}}{{2.0,{{06}^2}}} = 2,{5.10^5}V/m\)
Cho \({q_1} = {\rm{ }}{4.10^{ - 10}}C,{\rm{ }}{q_2} = {\rm{ }} - 4.{\rm{ }}{10^{ - 10}}C\), đặt tại $A$ và $B$ trong không khí biết $AB = 2 cm$. Xác định vectơ \(\vec E\) tại điểm $H$ - là trung điểm của $AB$.
-
A.
\({72.10^3}V/m\)
-
B.
\({36.10^3}V/m\)
-
C.
\(0{\rm{ }}V/m\)
-
D.
\({36.10^5}V/m\)
Đáp án : A
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
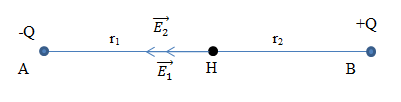
- Gọi cường độ điện trường do \({q_1}\) gây ra là \({E_1}\); do \({q_2}\) gây ra là \({E_2}\)
- Theo nguyên lí chồng chất điện trường:\(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
Vì \({E_1}\), \({E_2}\) là 2 véc tơ cùng phương, cùng chiều nên: $E = E_1 + E_2$
Ta có, cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Thay \({q_1} = {\rm{ }}{4.10^{-10}}C,{\rm{ }}{q_2} = {\rm{ }} - {4.10^{ - 10}}C,{\rm{ }}{r_1} = {\rm{ }}{r_2} = 1cm{\rm{ }},\varepsilon = 1\)
Ta có: \({E_1} = {\rm{ }}{E_2} = {36.10^3}V/m\)
\( = > E{\rm{ }} = {\rm{ }}2.{E_1} = 72.{\rm{ }}{10^3}V/m\)
Cho ${q_1} = {\rm{ }}{4.10^{ - 10}}C,{\rm{ }}{q_2} = {\rm{ }} - 4.{\rm{ }}{10^{ - 10}}C$, đặt tại A và B trong ko khí biết $AB{\rm{ }} = {\rm{ }}2{\rm{ }}cm$. Xác định vectơ $\vec E$tại điểm $M$, biết $MA{\rm{ }} = {\rm{ }}1{\rm{ }}cm,{\rm{ }}MB{\rm{ }} = {\rm{ }}3{\rm{ }}cm$.
-
A.
${72.10^3}V/m$
-
B.
${32.10^3}V/m$
-
C.
$0{\rm{ }}V/m$
-
D.
${40.10^3}V/m$
Đáp án : B
+ Áp dụng nguyên lí chồng chất điện trường: $\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} $
+ Áp dụng biểu thức xác định cường độ điện trường: $E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}$
- Gọi cường độ điện trường do ${q_1}$ gây ra là ${E_1}$ ; do ${q_2}$ gây ra là ${E_2}$
- Theo nguyên lí chồng chất điện trường:$\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} $
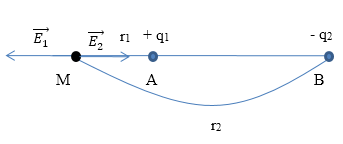
Vì ${E_1},{\rm{ }}{E_2}$ là 2 véc tơ cùng phương, ngược chiều nên: $E{\rm{ }} = {\rm{ }}{E_1} - {\rm{ }}{E_2}$
Ta có, cường độ điện trường: $E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}$
Thay ${q_1} = {\rm{ }}{4.10^{ - 10}}C,{\rm{ }}{q_2} = {\rm{ }} - {4.10^{ - 10}}C,{\rm{ }}{r_1} = {\rm{ }}1cm{\rm{ }},{r_2} = {\rm{ }}3cm,\varepsilon = 1$
Ta có:
${E_1} = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r_1}^2}} = {9.10^9}\dfrac{{\left| {{{4.10}^{ - 10}}} \right|}}{{1.0,{{01}^2}}} = {36.10^3}V/m$
${E_2} = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r_2}^2}} = {9.10^9}\dfrac{{\left| {{{4.10}^{ - 10}}} \right|}}{{1.0,{{03}^2}}} = {4.10^3}V/m$
$ = > E{\rm{ }} = {\rm{ }}{E_1} - {\rm{ }}{E_2} = 32.{\rm{ }}{10^3}V/m$
Cho q1 = 4.10-10 C, q2 = -4. 10-10 C, đặt tại A và B trong ko khí biết AB = 2 cm. Xác định vectơ \(\vec E\) tại điểm N, biết rằng NAB là một tam giác đều.
-
A.
32.103 V/m
-
B.
2.103 V/m
-
C.
9.103 V/m
-
D.
3.103 V/m
Đáp án : C
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
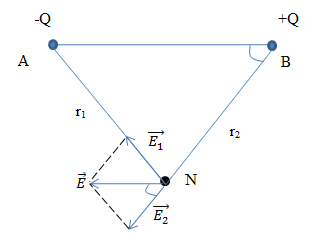
Ta có: |q1| = |q2| và r1 = r2 => E1 = E2
Vẽ hình ta có:
E = E1 = E2 = \(E = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon .{r^2}}} = {9.10^9}\frac{{\left| {{{4.10}^{ - 10}}} \right|}}{{1.0,{{02}^2}}} = {9.10^3}V/m\)
Hai điện tích q1 = 8. 10-8 C, q2 = -8. 10-8 C đặt tại A và B trong không khí biết AB = 4 cm. Tìm vectơ cường độ điện trường tại C trên đường trung trực của AB và cách AB 2 cm?
-
A.
18.105 V/m
-
B.
9.105 V/m
-
C.
12,73.105 V/m
-
D.
0 V/m
Đáp án : C
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
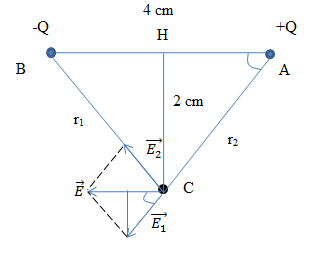
- Ta có: r1 = r2 = \(r = \sqrt {A{H^2} + A{C^2}} = 2\sqrt 2 \) cm Vì |q1| = |q2| và r1 = r2 => E1 = E2
- Từ hình vẽ ta có: \(E = 2{E_1}c{\rm{os}}\alpha \)
Với
\(\cos \alpha = \frac{{AH}}{{AC}} = \frac{2}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) => \(E = 2{E_1}\frac{{\sqrt 2 }}{2} = {E_1}\sqrt 2 \)
Ta có:
\({E_1} = k\frac{{\left| {{q_2}} \right|}}{{\varepsilon .{r_1}^2}} = {9.10^9}\frac{{\left| {{{8.10}^{ - 8}}} \right|}}{{1.{{(2.\sqrt 2 {{.10}^{ - 2}})}^2}}} = {9.10^5}V/m\)
=> E ≈ 12,73. 105 V/m.
Tại ba đỉnh của tam giác ABC vuông tại A, AB = 30cm, AC = 40cm và BC = 50cm. Đặt các điện tích q1 = q2 = q3 = 10-9 C. Xác định độ lớn cường độ điện trường tại điểm H- là chân đường cao kẻ từ A.
-
A.
156,25 V/m
-
B.
246 V/m
-
C.
259 V/m
-
D.
290 V/m
Đáp án : B
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Gọi \(\overrightarrow {{E_A}} ,\overrightarrow {{E_B}} ,\overrightarrow {{E_C}} \) lần lượt là cường độ điện trường do điện tích q1, q2 và q3 gây ra tại H.
Ta có :
\(\left\{ \begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{{30}^2}}} + \frac{1}{{{{40}^2}}} \to HA = 24cm\\BH = 18cm,CH = 32cm\end{array} \right.\)
Mặt khác : \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
\( \to \left\{ \begin{array}{l}{E_A} = k\frac{{\left| q \right|}}{{A{H^2}}} = {9.10^9}\frac{{{{10}^{ - 9}}}}{{0,{{24}^2}}} = 156,25V/m\\{E_B} = k\frac{{\left| q \right|}}{{B{H^2}}} = {9.10^9}\frac{{{{10}^{ - 9}}}}{{0,{{18}^2}}} = 277,78V/m\\{E_C} = k\frac{{\left| q \right|}}{{C{H^2}}} = {9.10^9}\frac{{{{10}^{ - 9}}}}{{0,{{32}^2}}} = 87,89V/m\end{array} \right.\)
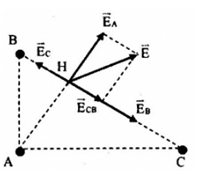
Cường độ điện trường tổng hợp tại H:
\(\overrightarrow E = \overrightarrow {{E_A}} + \overrightarrow {{E_B}} + \overrightarrow {{E_C}} \)
Ta có:
\(\overrightarrow {{E_B}} \uparrow \downarrow \overrightarrow {{E_C}} \to {E_{BC}} = {E_B} - {E_C} = 189,89V/m\)
\( \to E = \sqrt {E_A^2 + E_{BC}^2} = \sqrt {156,{{25}^2} + 189,{{89}^2}} = 245,91V/m\)
Bốn điểm A, B, C, D trong không khí tạo thành hình chữ nhật ABCD cạnh AD = 3cm; AB = 4cm. Các điện tích q1, q2, q3 đặt lần lượt tại A, B, C. Gọi \(\overrightarrow {{E_2}} \) là véctơ cường độ điện trường do điện tích q2 gây ra tại D. \(\overrightarrow {{E_{13}}} \)là cường độ điện trường tổng hợp do các điện tích q1 và q3 gây ra tại D. Xác định giá trị của q1 và q3 biết q2 = -12,5.10-8C và \(\overrightarrow {{E_{13}}} = \overrightarrow {{E_2}} \)
-
A.
q1 = -2,7.10-8C, q3 = -6,4.10-8C
-
B.
q1 = 2,7.10-8C, q3 = 6,4.10-8C
-
C.
q1 = -6,4.10-8C , q3 = -2,7.10-8C
-
D.
q1 = 6,4.10-8C , q3 = -2,7.10-8C
Đáp án : A
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Gọi \(\overrightarrow {{E_A}} ,\overrightarrow {{E_B}} ,\overrightarrow {{E_C}} \) lần lượt là cường độ điện trường do điện tích q1, q2 và q3 gây ra tại D.
Ta có: q2 < 0 => \(\overrightarrow {{E_2}} \) hướng về B
Theo đề bài, ta có: \(\overrightarrow {{E_{13}}} = \overrightarrow {{E_2}} \)=> \(\overrightarrow {{E_{13}}} \)phải cùng chiều và có độ lớn bằng \(\overrightarrow {{E_2}} \). Do đó, \(\overrightarrow {{E_1}} ,\overrightarrow {{E_3}} \)và \(\overrightarrow {{E_{13}}} \)có phương, chiều như hình vẽ:
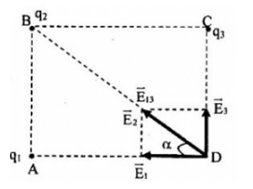
Từ hình vẽ, ta có:
Với \(\left\{ \begin{array}{l}{\rm{cos}}\alpha {\rm{ = }}\frac{{AD}}{{\sqrt {A{D^2} + A{B^2}} }} = \frac{3}{{\sqrt {{3^2} + {4^2}} }} = \frac{3}{5}\\\sin \alpha = \frac{{AB}}{{\sqrt {A{D^2} + A{B^2}} }} = \frac{4}{{\sqrt {{3^2} + {4^2}} }} = \frac{4}{5}\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{B{D^2}}} = {9.10^9}\frac{{\left| { - 12,{{5.10}^{ - 8}}} \right|}}{{0,{{05}^2}}} = {45.10^4}V/m\end{array} \right.\)
Ta suy ra:
\(\left\{ \begin{array}{l}{E_1} = {E_2}{\rm{cos}}\alpha = {45.10^4}.\frac{3}{5} = {27.10^4}V/m\\{E_3} = {E_2}\sin \alpha = {45.10^4}.\frac{4}{5} = {36.10^4}V/m\end{array} \right.\)
Mặt khác:
\(\left\{ \begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{A{D^2}}} = {27.10^4}V/m\\{E_3} = k\frac{{\left| {{q_1}} \right|}}{{C{D^2}}} = {36.10^4}V/m\end{array} \right. \to \left\{ \begin{array}{l}\left| {{q_1}} \right| = 2,{7.10^{ - 8}}C\\\left| {{q_2}} \right| = 6,{4.10^{ - 8}}C\end{array} \right.\)
Ta thấy, \(\overrightarrow {{E_1}} ,\overrightarrow {{E_3}} \)hướng lại gần các điện tích nên q1 và q3 sẽ là các điện tích âm
\( \to \left\{ \begin{array}{l}{q_1} = - 2,{7.10^{ - 8}}C\\{q_2} = - 6,{4.10^{ - 8}}C\end{array} \right.\)
Cho hai điện tích q1 = 1nC, q2 = -8nC đặt tại hai điểm A, B cách nhau 30cm trong chân không. Tìm điểm C cách A và B bao nhiều sao cho tại đó\(\overrightarrow {{E_2}} = 2\overrightarrow {{E_1}} \)
-
A.
CA = 20cm, CB = 20cm
-
B.
CA = 20cm, CB = 10cm
-
C.
CA = 15cm, CB = 15cm
-
D.
CA = 10cm, CB = 20cm
Đáp án : D
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Ta có :
\(\overrightarrow {{E_2}} = 2\overrightarrow {{E_1}} \)=> \(\overrightarrow {{E_2}} \uparrow \uparrow \overrightarrow {{E_1}} \)=> điểm C thuộc đường thẳng AB
Lại có q1 và q2 trái dấu => C nằm trong đoạn AB
=> CA + CB = AB = 30cm. (1)
Mặt khác,
\(\left\{ \begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{C{A^2}}}\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{C{B^2}}}\end{array} \right. \to \frac{{{E_1}}}{{{E_2}}} = \frac{{\left| {{q_1}} \right|C{B^2}}}{{\left| {{q_2}} \right|C{A^2}}} = \frac{1}{2} \to \frac{{CA}}{{CB}} = \sqrt {2\frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}} = \sqrt {2\frac{{\left| {{{10}^{ - 9}}} \right|}}{{\left| { - {{8.10}^{ - 9}}} \right|}}} = \frac{1}{2}\) (2)
Từ (1) và (2) ta suy ra: CA = 10cm, CB = 20cm
Hai điện tích điểm q1 = 4.10-6C; q2 = 36.10-6C đặt tại hai điểm cố đinh A và B trong dầu có hằng số điện môi ε = 2. AB = 16cm. Xác định vị trí của điểm M mà tại đó cường độ điện trường tổng hợp bằng không?
-
A.
MA = 4cm, MB = 12cm
-
B.
MA = 12cm, MB = 4cm
-
C.
MA = 8cm, MB = 8cm
-
D.
MA = 4cm, MB = 20cm
Đáp án : A
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} \)lần lượt là cường độ điện trường do q1 và q2 gây ra tại M.
Theo đề bài ta có:
\(\overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \to \overrightarrow {{E_1}} = \overrightarrow { - {E_2}} \to \overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \)=> M phải thuộc AB
Và vì 2 điện tích cùng dấu => M phải ở bên trong AB
Mặt khác: \(\left\{ \begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon M{A^2}}}\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{\varepsilon M{B^2}}}\end{array} \right. \to \frac{{{E_1}}}{{{E_2}}} = \frac{{\left| {{q_1}} \right|M{B^2}}}{{\left| {{q_2}} \right|M{A^2}}} = 1 \to \frac{{MA}}{{MB}} = \sqrt {\frac{{\left| {{q_1}} \right|}}{{\left| {{q_2}} \right|}}} = \sqrt {\frac{{\left| {{{4.10}^{ - 6}}} \right|}}{{\left| {{{36.10}^{ - 6}}} \right|}}} = \frac{1}{3}\)
Lại có: MA + MB = 16
=> MA = 4cm, MB = 12cm
Cho hình vuông ABCD cạnh a, tại A và C đặt các điện tích q1 = q3 = q > 0. Cần đặt ở B điện tích bằng bao nhiêu để cường độ điện trường ở D bằng 0.
-
A.
\( - 2\sqrt 2 q\)
-
B.
\(2\sqrt 2 q\)
-
C.
\( - 2q\)
-
D.
\(2q\)
Đáp án : A
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Ta có :
\(\left\{ \begin{array}{l}{E_1} = {E_3} = k\frac{{{q^2}}}{{{a^2}}}\\{E_{13}} = \sqrt {E_1^2 + E_3^2} = \sqrt 2 {E_1}\end{array} \right.\)
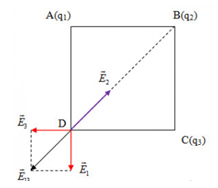
Để \({E_D} = 0 \to \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \to \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \to {q_2} < 0\\{E_{13}} = {E_2}\end{array} \right.\)
\({E_2} = {E_{13}} \leftrightarrow {E_2} = \sqrt 2 {E_1} \leftrightarrow k\frac{{\left| {{q_2}} \right|}}{{{{\left( {a\sqrt 2 } \right)}^2}}} = k\frac{{\sqrt 2 \left| {{q_1}} \right|}}{{{{\left( a \right)}^2}}} \to \left| {{q_2}} \right| = 2\sqrt 2 \left| {{q_1}} \right| \to {q_2} = - 2\sqrt 2 q\)
Một quả cầu nhỏ mang điện tích được cân bằng trong điện trường do tác dụng của trọng lực và lực điện trường. Đột ngột giảm độ lớn điện trường đi còn một nửa nhưng vẫn giữ nguyên phương và chiều của đường sức điện. Thời gian để quả cầu di chuyển được 5cm trong điện trường. Lấy g = 10m/s2
-
A.
0,1s
-
B.
0,071s
-
C.
0,173s
-
D.
0,141s
Đáp án : D
+ Xác định các lực tác dụng lên vật
+ Áp dụng điều kiện cân bằng của vật
+ Áp dụng biểu thức tính lực điện: F = qE
+ Áp dụng định luật II-Newton
+ Sử dụng phương trình chuyển động: \(s = \frac{1}{2}a{t^2}\)
Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) lần lượt là lực điện trường lúc đầu và lúc sau.
+ Các lực tác dụng lên quả cầu gồm trọng lực \(\overrightarrow P \) và lực điện \(\overrightarrow F \)
+ Lúc đầu quả cầu cân bằng: \(\overrightarrow P + \overrightarrow {{F_1}} = 0 \to mg = qE\)
+ Khi độ lớn điện trường giảm đi một nửa thì : \({F_2} = \frac{{qE}}{2} = \frac{{mg}}{2}\)
Áp dụng định luật II-Newton, ta có:
\(\overrightarrow P + \overrightarrow {{F_2}} = m\overrightarrow a \)
Chọn chiều dương hướng xuống,
\( \to mg - {F_2} = ma \to a = \frac{{mg - \frac{{mg}}{2}}}{m} = \frac{g}{2}\)
Lại có:
\(s = \frac{1}{2}a{t^2} \to t = \sqrt {\frac{{2{\rm{s}}}}{a}} = \sqrt {\frac{{2.0,05}}{{\frac{{10}}{2}}}} = \frac{{\sqrt 2 }}{{10}} \approx 0,1414{\rm{s}}\)
Cho hai tấm kim loại song song, nằm ngang, nhiễm điện trái dấu. Khoảng không gian giữa hai tấm kim loại chứa đầy dầu. Điện trường giữa hai tấm kim loại là điện trường đều hướng từ trên xuống và có độ lớn 20000V/m. Một quả cầu bằng sắt có bán kính 1cm mang điện tích q nằm lơ lửng ở khoảng không gian giữa hai tấm kim loại. Điện tích q có giá trị bằng bao nhiểu? Biết khối lượng riêng của sắt là 7800kg/m3, của dầu là 800kg/m3. Lấy g = 10m/s2.
-
A.
q = -4.10-6C
-
B.
q = 4.10-6C
-
C.
q = -14,7.10-6C
-
D.
q = 14,7.10-6C
Đáp án : C
+ Xác định các lực tác dụng lên vật
+ Áp dụng điều kiện cân bằng của vật
+ Áp dụng biểu thức tính lực đẩy acsimét: FA= ρVg
+ Áp dụng biểu thức tính cường độ điện trường: \(E = \frac{F}{q}\)
Các lực tác dụng lên quả cầu gồm: lực điện \(\overrightarrow F \) , trọng lực \(\overrightarrow P \)hướng xuống và lực đẩy Acsimét \(\overrightarrow {{F_A}} \)hướng lên.
+ Điều kiện cân bằng của quả cầu: \(\overrightarrow P + \overrightarrow F + \overrightarrow {{F_A}} = 0\)
\(\left\{ \begin{array}{l}P = mg = {\rho _{vat}}Vg = {\rho _{vat}}\frac{4}{3}\pi {R^3}g\\{F_A} = {\rho _{mt}}Vg = {\rho _{mt}}\frac{4}{3}\pi {R^3}g\end{array} \right.\)
Ta có khối lượng riêng của vật lớn hơn \( \to P > {F_A} \to F = P - {F_A}\)
\(\begin{array}{l}F = P - {F_A} \leftrightarrow \left| q \right|E = P - {F_A}\\ \to \left| q \right| = \dfrac{{P - {F_A}}}{E} = \dfrac{{\dfrac{4}{3}\pi {R^3}\left( {{\rho _{vat}} - {\rho _{mt}}} \right)}}{E} = 14,{7.10^{ - 6}}C\end{array}\)
=> Để vật cân bằng thì lực điện phải hướng lên
Ta có, lực ngược hướng với \(\overrightarrow E \) => q < 0
=> q = -14,7.10-6C
Một con lắc đơn gồm một quả cầu tích điện dương khối lượng \(\sqrt 3 g\) buộc vào sợi dây mảnh cách điện. Con lắc treo trong điện trường đều có phương nằm ngang với cường độ điện trường 10000 V/m. Tại nơi có g = 9,8m/s2. Khi vật ở vị trí cân bằng, sợi dây lệch một góc α = 300 so với phương thẳng đứng. Độ lớn của điện tích của quả cầu là?
-
A.
4.10-7C
-
B.
3,27.10-7C
-
C.
9,8.10-7C
-
D.
10-7C
Đáp án : C
+ Xác định các lực tác dụng lên vật
+ Áp dụng điều kiện cân bằng của vật
+ Áp dụng biểu thức tính lực điện: F = qE
+ Vận dụng công thức lượng giác.
Các lực tác dụng lên quả cầu gồm: lực điện \(\overrightarrow F \) , trọng lực \(\overrightarrow P \)hướng xuống và lực căng dây \(\overrightarrow T \).
Khi quả cầu cân bằng:
\(\overrightarrow T + \overrightarrow P + \overrightarrow F = 0 \to \overrightarrow T + \overrightarrow {P'} = 0\)
=> P‘ có phương sợi dây P‘ tạo với P một góc α = 300
Từ hình ta có:
\(\tan \alpha = \frac{F}{P} = \frac{{\left| q \right|E}}{{mg}} = \tan {30^0} \to \left| q \right| = \frac{{mg\tan {{30}^0}}}{E} = \frac{{\sqrt 3 {{.10}^{ - 3}}.9,8.\tan {{30}^0}}}{{10000}} = 9,{8.10^{ - 7}}C\)
Đặt tại $6$ đỉnh của lục giác đều các điện tích $q$, $-2q$, $3q$, $4q$, $-5q$ và $q'$. Xác định $q'$ theo $q$ để cường độ điện trường tại tâm O của lục giác bằng $0$ biết $q > 0$.
-
A.
$q'= -6q$
-
B.
$q'= 6q$
-
C.
$q'=-q$
-
D.
$q'= q$
Đáp án : B
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Gọi
+ \(\overrightarrow {{E_{3q}}} \) là điện trường tổng hợp tại O do $q$ và $4q$ gây ra.
+ \(\overrightarrow {{E_{ - 3q}}} \) là điện trường tổng hợp tại O do $-5q$ và $-2q$ gây ra.
+ \(\overrightarrow {{E_3}} \) là điện trường tổng hợp tại O do $q$ và $4q$ gây ra.
Các véctơ được biểu diễn như hình.
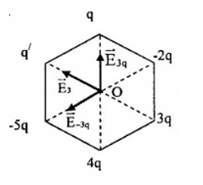
Ta có: \(\overrightarrow {{E_0}} = \overrightarrow {{E_{ - 3q}}} + \overrightarrow {{E_{3q}}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{ - 33}}} + \overrightarrow {{E_3}} \)
Vì => \(\overrightarrow {{E_{ - 33}}} \) cùng chiều \(\overrightarrow {{E_3}} \)
Ta có: \(\left\{ \begin{array}{l}{E_{ - 33}} = {E_3}\\\overrightarrow E = \overrightarrow {{E_{ - 33}}} + \overrightarrow {{E_3}} \end{array} \right. \to E = 2{E_3} = 2k\frac{{3q}}{{{r^2}}} = k\frac{{6q}}{{{r^2}}}\)
Để tại O cường độ điện trường tổng hợp bằng 0 thì:
\(\overrightarrow {{E_{q'}}} + \overrightarrow E = 0 \to \left\{ \begin{array}{l}\overrightarrow {{E_{q'}}} \uparrow \downarrow \overrightarrow E \to q' > 0\\{E_{q'}} = E \leftrightarrow k\dfrac{{\left| {q'} \right|}}{{{r^2}}} = k\dfrac{{6q}}{{{r^2}}} \to \left| {q'} \right| = 6q\end{array} \right. \to q' = 6q\)
Cường độ điện trường của một điện tích phụ thuộc vào khoảng cách r được mô tả như đồ thị bên. Biết \({r_2} = \dfrac{{{r_1} + {r_3}}}{2}\)và các điểm cùng nằm trên một đường sức. Giá trị của x bằng
-
A.
\(13,5 V/m\)
-
B.
\(17 V/m\)
-
C.
\(22,5 V/m\)
-
D.
\(16 V/m\)
Đáp án : D
Áp dụng biểu thức tính độ lớn cường độ điện trường: \(E = \dfrac{{k\left| Q \right|}}{{{r^2}}}\)
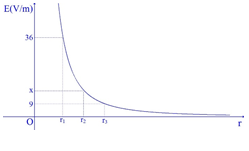
Ta có: \(E = \dfrac{{k\left| Q \right|}}{{{r^2}}} \Rightarrow E\sim\dfrac{1}{{{r^2}}} \Leftrightarrow r\sim\dfrac{1}{{\sqrt E }}\)
\( \Rightarrow {r_2} = \dfrac{{{r_1} + {r_3}}}{2} \Rightarrow \dfrac{2}{{\sqrt {{E_2}} }} = \dfrac{1}{{\sqrt {{E_1}} }} + \dfrac{1}{{\sqrt {{E_3}} }} \Rightarrow {E_2} = x = 16\) (V/m)
Hai điện tích điểm \({q_1} = - 9\mu C,{\rm{ }}{q_2} = 4\mu C\) đặt lần lượt tại A,B có thể tìm thấy vị trí của điểm M mà tại đó điện trường tổng hợp bằng không trên
-
A.
Đường trung trực của AB
-
B.
Đường thẳng AB, nằm ngoài đoạn thằng AB về phía A
-
C.
Đường thẳng AB, nằm ngoài đoạn thẳng AB về phía B
-
D.
Đoạn thẳng AB, vị trí bất kỳ
Đáp án : C
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
- Nếu \({q_1};{q_2}\) cùng dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm trong \({q_1};{q_2}\)
- Nếu \({q_1};{q_2}\) trái dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm ngoài \({q_1};{q_2}\)
Và M nằm gần điện tích có độ lớn nhỏ hơn.
Cường độ điện trường tổng hợp tại M:
\(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Do \({q_1};{q_2}\) trái dấu, để \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \) thì M nằm ngoài \({q_1};{q_2}\)
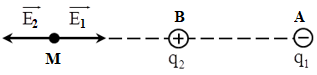
Lại có \(\left\{ \begin{array}{l}{q_1} = - 9\mu C\\{q_2} = 4\mu C\end{array} \right. \Rightarrow \left| {{q_1}} \right| > \left| {{q_2}} \right| \Rightarrow \) M nằm gần điện tích có độ lớn nhỏ hơn, tức là gần B hơn.
Đặt 4 điện tích âm có cùng độ lớn \(q\) tại 4 đỉnh của một hình vuông ABCD cạnh \(a.\) Xác định cường độ tổng hợp tại giao điểm hai đường chéo của hình vuông.
-
A.
\({E_O} = 2.\dfrac{{k\left| q \right|}}{{{a^2}}}\)
-
B.
\(0\)
-
C.
\({E_O} = 4.\dfrac{{k\left| q \right|}}{{{a^2}}}\)
-
D.
\({E_O} = \dfrac{2}{{\sqrt 3 }}.\dfrac{{k\left| q \right|}}{{{a^2}}}\)
Đáp án : B
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường, áp dụng định lí hàm số cos và nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Biểu diễn các vecto cường độ điện trường gây ra tại O trên hình vẽ:
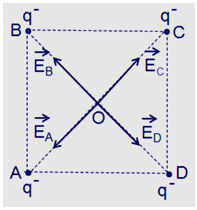
Ta có: \(\overrightarrow {{E_O}} = \overrightarrow {{E_A}} + \overrightarrow {{E_B}} + \overrightarrow {{E_C}} + \overrightarrow {{E_D}} \)
Với: \({E_A} = {E_B} = {E_C} = {E_D} = \dfrac{{k\left| q \right|}}{{O{A^2}}}\)
Do \(\left\{ \begin{array}{l}\overrightarrow {{E_A}} \uparrow \downarrow \overrightarrow {{E_C}} \\{E_A} = {E_C}\end{array} \right. \Rightarrow \overrightarrow {{E_{AC}}} = \overrightarrow {{E_A}} + \overrightarrow {{E_C}} = 0\)
Do \(\left\{ \begin{array}{l}\overrightarrow {{E_B}} \uparrow \downarrow \overrightarrow {{E_D}} \\{E_B} = {E_D}\end{array} \right. \Rightarrow \overrightarrow {{E_{BD}}} = \overrightarrow {{E_B}} + \overrightarrow {{E_D}} = 0\)
Cường độ điện tường tổng hợp tại O là:
\(\overrightarrow {{E_O}} = \left( {\overrightarrow {{E_A}} + \overrightarrow {{E_C}} } \right) + \left( {\overrightarrow {{E_B}} + \overrightarrow {{E_D}} } \right) = 0\)
Tại hai điểm A và B cách nhau \(10cm\) trong không khí có đặt hai điện tích \(q_1 = q_2 = 16.10^{ - 8}C.\) Xác định cường độ điện trường do hai điện tích điểm này gây ra tại C biết \(AC = BC = 8cm.\)
-
A.
\(3,{51.10^5}(V/m)\)
-
B.
\(5,{25.10^5}(V/m)\)
-
C.
\(2,{5.10^5}(V/m)\)
-
D.
\(3,{2.10^5}(V/m)\)
Đáp án : A
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường :\(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
Ta có \(AC = BC = 8 cm\) và \(AB = 10 cm\) nên C nằm trên đường trung trực của AB.
Cường độ điện trường tổng hợp tại C: \({\vec E_C} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} {\rm{ }}\)
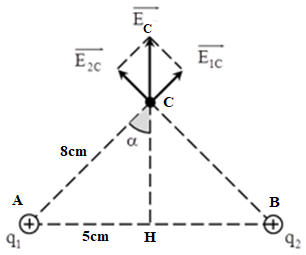
Ta có: \({E_1} = {E_2} = \dfrac{{k.\left| {{q_1}} \right|}}{{A{C^2}}} = \dfrac{{{{9.10}^9}{{.16.10}^{ - 8}}}}{{0,{{08}^2}}} = 2,{25.10^5}V/m\)
Từ hình vẽ ta có: \(E_C = 2E_1\cos \alpha = 2E_1.\dfrac{\sqrt{AC^2 - AH^2}}{AC}\)
\(\Rightarrow E_C = 2.2,25.10^5.\dfrac{\sqrt{8^2 - 5^2}}{8} = 3,51.10^5\,\,\left ( V/m \right )\)
Cho hai điện tích điểm \({q_1} = {6.10^{ - 7}}C;{q_2} = - {8.10^{ - 7}}C\) đặt tại hai điểm A và B trong không khí cách nhau \(5cm.\) Xác định véc tơ cường độ điện trường tổng hợp tại M do \({q_1}\) và \({q_2}\) gây ra tại M biết \(MA = 3cm, MB = 8cm.\)
-
A.
\(71,{25.10^5}V/m\)
-
B.
\(48,{75.10^5}V/m\)
-
C.
\(61,{05.10^5}V/m\)
-
D.
\(35,{63.10^5}V/m\)
Đáp án : B
Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
Vẽ hình biểu điễn vecto cường độ điện trường và áp dụng nguyên lí chồng chất điện trường: \(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Cường độ điện trường do điện tích \({q_1}\) gây ra tại M:
\({E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{M^2}}} = {9.10^9}\dfrac{{\left| {{{6.10}^{ - 7}}} \right|}}{{0,{{03}^2}}} = {60.10^5}V/m\)
+ Cường độ điện trường do điện tích \({q_2}\) gây ra tại M:
\({E_2} = k\dfrac{{\left| {{q_2}} \right|}}{{B{M^2}}} = {9.10^9}\dfrac{{\left| { - {{8.10}^{ - 7}}} \right|}}{{0,{{08}^2}}} = 11,{25.10^5}V/m\)
Cường độ điện trường tổng hợp tại M: \(\vec E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} {\rm{ }}\)
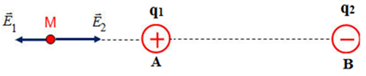
Từ hình vẽ ta có: \(\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \Rightarrow E = \left| {{E_1} - {E_2}} \right|\)
\( \Rightarrow E = \left| {{{60.10}^5} - 11,{{25.10}^5}} \right| = 48,{75.10^5}V/m\)
Một quả cầu kim loại nhỏ có khối lượng 1g được tích điện q = 10-5C treo vào đầu một sợi dây mảnh và đặt trong điện trường đều E. Khi quả cầu đứng cân bằng thì dây treo hợp với phương thẳng một góc 600, lấy g = 10m/s2. Tìm E.
-
A.
1520V/m
-
B.
1732V/m
-
C.
1341 V/m
-
D.
1124 V/m
Đáp án : B
Phân tích các lực tác dụng lên quả cầu.
Công thức tính lực điện và trọng lượng: \(\left\{ \begin{array}{l}F = qE\\P = mg\end{array} \right.\)
Sử dụng tỉ số lượng giác trong tam giác vuông suy ra E.
Phân tích các lực tác dụng vào quả cầu ta có :
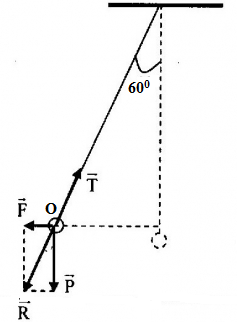
Từ hình vẽ ta có : \(\widehat {ROP} = {60^0}\)
Tam giác ROT vuông tại O, có :
\(\begin{array}{l}\tan \widehat {ROP} = \dfrac{F}{P} \Leftrightarrow \tan {60^0} = \dfrac{{\left| q \right|.E}}{{m.g}}\\ \Rightarrow E = \dfrac{{mg.\tan 60}}{{\left| q \right|}} = \dfrac{{{{10}^{ - 3}}.10.\tan 60}}{{{{10}^{ - 5}}}} = 1732V/m\end{array}\)
Cho hình vuông ABCD, tại A và C đặt các điện tích \(q_1 = q_3 = q = 2,5.10^{ - 8}C.\) Hỏi phải đặt tại B một điện tích bao nhiêu để cường độ điện trường tại D bằng \(0.\)
-
A.
\( - 5\sqrt 2 {.10^{ - 8}}C\)
-
B.
\(5\sqrt 2 {.10^{ - 8}}C\)
-
C.
\({5.10^{ - 8}}C\)
-
D.
\( - {5.10^{ - 8}}C\)
Đáp án : A
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
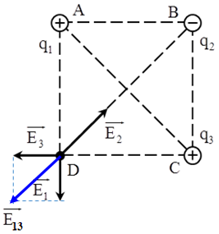
+ Cường độ điện trường tổng hợp tại D:\(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
Trong đó \(\overrightarrow {{E_1}} ;\overrightarrow {{E_2}} ;\overrightarrow {{E_3}} \) lần lượt là vecto cường độ điện trường do các điện tích \({q_1};{q_2};{q_3}\) gây ra tại D.
+ Vì \(\left\{\begin{matrix} q_1 = q_3 \\ AD = CD \end{matrix}\right. \Rightarrow E_1 = E_3 \Rightarrow E_{13} = \sqrt {2}E_1 = \sqrt {2}.\dfrac{k\left | q \right |}{a^2}\)
+ Ta có: \(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} \)
Để cường độ điện trường tại O triệt tiêu thì:
\(\overrightarrow {{E_D}} = 0 \Leftrightarrow \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_{13}} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ (1) \( \Rightarrow \overrightarrow {{E_2}} \) hướng lại gần \({q_2} \Rightarrow {q_2} < 0\)
Từ (2) ta có:
\({E_2} = {E_{13}} \Leftrightarrow \dfrac{{k\left| {{q_2}} \right|}}{{{{\left( {a\sqrt 2 } \right)}^2}}} = \sqrt 2 .\dfrac{{k\left| q \right|}}{{{a^2}}} \Rightarrow \left| {{q_2}} \right| = 2\sqrt 2 .\left| q \right| = 2\sqrt 2 \left| q \right|\)
\(q_2 = - 2\sqrt{2}.2,5.10^{ - 8}C = - 5\sqrt{2}.10^{ - 8}C.\)
Bốn điểm A, B, C, D trong không khí tạo thành hình chữ nhật ABCD cạnh \(AD = a = 3cm;AB = b = 4cm\). Các điện tích \(q_1\,;\,q_2\,;\,q_3\)được đặt lần lượt tại A, B, C. Biết \(q_2 = - 12,5.10^{ - 8}C\) và cường độ điện trường tổng hợp tại D bằng \(0.\) Tính \({q_1};{q_2}\)?
-
A.
\({q_1} = - 6,{4.10^{ - 8}}C;{q_3} = 2,{7.10^{ - 8}}C\)
-
B.
\({q_1} = 2,{7.10^{ - 8}}C;{q_3} = - 6,{4.10^{ - 8}}C\)
-
C.
\({q_1} = 6,{4.10^{ - 8}}C;{q_3} = 2,{7.10^{ - 8}}C\)
-
D.
\({q_1} = 2,{7.10^{ - 8}}C;{q_3} = 6,{4.10^{ - 8}}C\)
Đáp án : D
+ Công thức tính cường độ điện trường: \(E = k.\dfrac{{\left| q \right|}}{{{r^2}}}\)
+ Điện trường tổng hợp tại M: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Điện trường tại M triệt tiêu khi: \(\overrightarrow {{E_M}} = 0\)
* Trường hợp: \(\overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \,\,\left( 1 \right)\\{E_1} = {E_2}\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
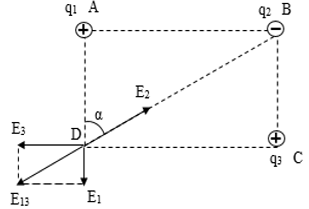
Vectơ cường độ điện trường tại D:
\(\overrightarrow {{E_D}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} \)
Do \(\overrightarrow {{E_D}} = 0 \Rightarrow \overrightarrow {{E_{13}}} + \overrightarrow {{E_2}} = 0 \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{E_{13}}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_{13}} = {E_2}\end{array} \right.\)
Vì nên \({q_1};{q_3}\) phải là điện tích dương.
Từ hình vẽ ta có:
\(\begin{array}{l}{E_1} = {E_{13}}\cos \alpha = {E_2}.\cos \alpha \Leftrightarrow k.\dfrac{{\left| {{q_1}} \right|}}{{A{D^2}}} = k.\dfrac{{\left| {{q_2}} \right|}}{{B{D^2}}}.\dfrac{{AD}}{{BD}}\\ \Rightarrow \left| {{q_1}} \right| = \dfrac{{A{D^3}}}{{B{D^3}}}.\left| {{q_2}} \right| = \dfrac{{A{D^3}}}{{{{\left( {\sqrt {A{D^2} + A{B^2}} } \right)}^3}}}.\left| {{q_2}} \right|\\ \Rightarrow {q_1} = \dfrac{{{3^3}}}{{{{\left( {\sqrt {{3^2} + {4^2}} } \right)}^3}}}.12,{5.10^{ - 8}} = 2,{7.10^{ - 8}}C\end{array}\)
Tương tự ta có:
\(\begin{array}{l}{E_3} = {E_{13}}\sin \alpha = {E_2}.sin\alpha \Leftrightarrow k.\dfrac{{\left| {{q_3}} \right|}}{{A{B^2}}} = k.\dfrac{{\left| {{q_2}} \right|}}{{B{D^2}}}.\dfrac{{AB}}{{BD}}\\ \Rightarrow \left| {{q_3}} \right| = \dfrac{{A{B^3}}}{{B{D^3}}}.\left| {{q_2}} \right| = \dfrac{{A{B^3}}}{{{{\left( {\sqrt {A{D^2} + A{B^2}} } \right)}^3}}}.\left| {{q_2}} \right|\\ \Rightarrow {q_3} = \dfrac{{{4^3}}}{{{{\left( {\sqrt {{3^2} + {4^2}} } \right)}^3}}}.12,{5.10^{ - 8}} = 6,{4.10^{ - 8}}C\end{array}\)
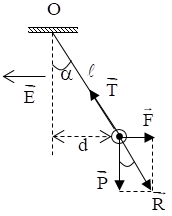
Một quả cầu khối lượng \(m = 4,{5.10^{ - 3}}kg\) treo vào một sợi dây dài \(2m.\) Quả cầu nằm trong điện trường có \(\overrightarrow E \) nằm ngang, hướng sang trái như hình vẽ. Biết \(d = 1m,E = 2000V/m\). Lấy \(g = 10{\rm{ }}m/{s^2}\).
Tính độ lớn của lực căng dây.
-
A.
\(0,09N\)
-
B.
\(0,052N\)
-
C.
\(0,045N\)
-
D.
\(0,156N\)
Đáp án : B
Phân tích các lực tác dụng lên quả cầu.
Công thức tính lực điện và trọng lượng: \(\left\{ {\begin{array}{*{20}{l}}{F = qE}\\{P = mg}\end{array}} \right.\)
Sử dụng tỉ số lượng giác trong tam giác vuông suy ra \(E.\)
Lực tác dụng vào quả cầu: \(\overrightarrow P ;\overrightarrow {{F_d}} ;\overrightarrow T \)
Biểu diễn các lực tác dụng vào quả cầu như hình vẽ:
Khi quả cầu cân bằng: \(\overrightarrow P + \overrightarrow {{F_d}} + \overrightarrow T = 0\)
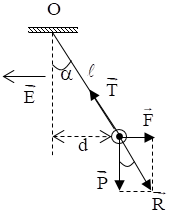
Đặt: \(\overrightarrow R = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow T + \overrightarrow R = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow T \uparrow \downarrow \overrightarrow R \\T = R\,\end{array} \right.\)
Từ hình vẽ ta có:
\(\cos \alpha = \dfrac{{\sqrt {{l^2} - {d^2}} }}{l} = \dfrac{P}{R} \Rightarrow R = P.\dfrac{l}{{\sqrt {{l^2} - {d^2}} }} = mg.\dfrac{l}{{\sqrt {{l^2} - {d^2}} }}\)
\( \Rightarrow R = 4,{5.10^{ - 3}}.10.\dfrac{2}{{\sqrt {{2^2} - {1^2}} }} = 0,052N\)
Vậy độ lớn lực căng dây: \(T = R = 0,052N\)
Một điện tích điểm \({q_1} = {4.10^{ - 6}}C\) đặt tại điểm A trong không khí.
Xác định độ lớn cường độ điện trường do q1 gây ra tại C cách A 10cm.
-
A.
\({3,6.10^5}V/m\)
-
B.
\({36.10^5}V/m\)
-
C.
\({18.10^5}V/m\)
-
D.
\({36.10^4}V/m\)
Đáp án: B
Độ lớn cường độ điện trường do q1 gây ra tại C là:
\({E_1} = k\dfrac{{\left| {{q_1}} \right|}}{{A{C^2}}} = {9.10^9}.\dfrac{{\left| {{{4.10}^{ - 6}}} \right|}}{{0,{1^2}}} = {36.10^5}V/m\)
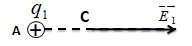
Tại điểm B đặt thêm \({q_2} = - {16.10^{ - 6}}C\). Biết AB = 40 cm; BC = 30 cm. Xác định cường độ điện trường tổng hợp do q1 và q2 gây ra tại điểm C.
-
A.
\({52.10^5}V/m\)
-
B.
\({20.10^5}V/m\)
-
C.
\({52.10^4}V/m\)
-
D.
\({20.10^4}V/m\)
Đáp án: A
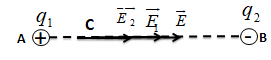
Ta có:
\({E_2} = k\frac{{\left| {{q_1}} \right|}}{{\varepsilon .B{C^2}}} = {9.10^9}.\frac{{\left| {{{16.10}^{ - 6}}} \right|}}{{0,{3^2}}} = {16.10^5}V/m\)
Cường độ điện trường tổng hợp do q1 và q2 gây ra tại C là:
\(\overrightarrow E = {\overrightarrow E _1} + {\overrightarrow E _2}\)
Có phương chiều được biểu diễn như hình vẽ.
Có độ lớn: \(E = {E_1} + {E_2} = {36.10^5} + {16.10^5} = {52.10^5}V/m\)
Tại một điểm trong không khí có hai cường độ điện trường có phương vuông góc với nhau và có độ lớn lần lượt là E1 = 6.104 V/m; E2 = 8.104 V/m. Độ lớn của điện trường tổng là:
-
A.
10.104 V/m
-
B.
14.104 V/m
-
C.
2. 104 V/m
-
D.
48.104 V/m
Đáp án : A
Độ lớn điện trường tổng hợp là:
\(E = \sqrt {E_1^2 + E_2^2} = \sqrt {{{\left( {{{6.10}^4}} \right)}^2} + {{\left( {{{8.10}^4}} \right)}^2}} = {10.10^4}V/m\)
Một quả cầu nhỏ m = 0,25g, mang điện tích q = 5.10-9 C treo trên sợi dây mảnh trong điện trường đều có phương nằm ngang, cường độ điện trường E = 106V/m cho g = 10m/s2. Độ lớn lực điện trường tác dụng lên quả cầu là
-
A.
7,5.10-5 N
-
B.
3.10-3 N
-
C.
5.10-3 N
-
D.
2,5.10-3 N
Đáp án : C
Quả cầu chịu tác dụng của lực căng \(\overrightarrow T \), trọng lực \(\overrightarrow P \) và lực điện trường \(\overrightarrow F \).
Lực căng \(\overrightarrow T \) và trọng lực \(\overrightarrow P \) là hai lực cân bằng.
Suy ra, độ lớn lực điện trường tác dụng lên quả cầu là:
\(F = E.q = {10^6}{.5.10^{ - 9}} = {5.10^{ - 3}}N\)
Một điện tích \(Q = 1,{6.10^{ - 8}}C\) gây ra một điện trường tại \(A\) có cường độ là \({9.10^4}\) V/m (\(Q\) và \(A\) đều đặt trong chân không). Điểm \(A\) cách \(Q\) một đoạn là
-
A.
1,6 cm
-
B.
16 cm
-
C.
4 cm
-
D.
40 cm
Đáp án : C
Sử dụng công thức tính điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon {r^2}}}\)
Ta có: \(E = k\frac{{\left| Q \right|}}{{\varepsilon {r^2}}} \Rightarrow r = \sqrt {\frac{{k\left| Q \right|}}{{\varepsilon E}}} \)
Điểm \(A\) cách \(Q\) một khoảng là:
\(r = \sqrt {\frac{{{{9.10}^9}.1,{{6.10}^{ - 8}}}}{{{{9.10}^4}}}} = 0,04{\mkern 1mu} {\mkern 1mu} \left( m \right) = 4{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\)
Hai điện tích điểm \({q_1} = {2.10^{ - 8}}C\) và \({q_2} = - {2.10^{ - 8}}C\) đặt tại hai điểm \(A\) và \(B\) cách nhau 30 cm trong không khí. Tại điểm C, cường độ điện trường tổng hợp do \({q_1}\) và \({q_2}\) gây ra bằng 2000 V/m. Chọn câu đúng về vị trí của điểm C.
-
A.
C thẳng hàng với A, B theo thứ tự A, B, C
-
B.
A, B, C tạo thành một tam giác đều
-
C.
C là trung điểm của đoạn AB
-
D.
C thẳng hàng với A, B theo thứ tự C, A, B
Đáp án : B
Sử dụng công thức tính điện trường: \(E = k\frac{{\left| q \right|}}{{\varepsilon {r^2}}}\)
Ta có: \({E_1} = k\frac{{\left| {{q_1}} \right|}}{{r_1^2}} = {9.10^9} \cdot \frac{{{{2.10}^{ - 8}}}}{{r_1^2}}\)
\({E_2} = k\frac{{\left| {{q_1}} \right|}}{{r_2^2}} = {9.10^9} \cdot \frac{{{{2.10}^{ - 8}}}}{{r_2^2}}\)
Ta thấy \(\left| {{q_1}} \right| = \left| {{q_2}} \right| \Rightarrow {r_1} = {r_2} \Rightarrow {E_1} = {E_2}\)
\( \Rightarrow \) Điểm \({\rm{C}}\) cách đều \({\rm{A}},{\rm{B}} \Rightarrow \) loại đáp án \({\rm{A}},{\rm{D}}\)
- Giả sử \({\rm{C}}\) là trung điểm \({\rm{AB}}\) thì: \({r_1} = {r_2} = 0,15m.\)
Khi đó: \({E_1} = {E_2} = k\frac{{\left| {{q_1}} \right|}}{{r_1^2}} = {9.10^9} \cdot \frac{{{{2.10}^{ - 8}}}}{{0,{{15}^2}}} = 8000\left( {{\rm{V}}/{\rm{m}}} \right)\)
Suy ra \(E = {E_1} + {E_2} = 2{{\rm{E}}_1} = 2.8000 = 16000 \ne 2000 \Rightarrow \) Loại \({\rm{C}}\)
- A, B, C tạo thành tam giác đều thì: \({r_1} = {r_2} = 0,3{\mkern 1mu} {\mkern 1mu} m\)
Khi đó: \({E_1} = {E_2} = k\frac{{\left| {{q_1}} \right|}}{{r_1^2}} = {9.10^9} \cdot \frac{{2 \cdot {{10}^{ - 8}}}}{{0,{3^2}}} = 2000{\mkern 1mu} {\mkern 1mu} \left( {V/m} \right)\)
Suy ra: \(E = \sqrt {E_1^2 + E_2^2 + 2{{\rm{E}}_1}{E_2}.\cos {{120}^0}} = 2000{\mkern 1mu} {\mkern 1mu} \left( {V/m} \right)\)
Vậy A, B, C tạo thành tam giác đều.
Một điện tích \( - 1{\mkern 1mu} \mu C\) đặt trong chân không sinh ra điện trường tại một điểm cách nó 1m có độ lớn và hướng là
-
A.
9000 V/m, hướng ra xa nó.
-
B.
\({9.10^9}\) V/m, hướng về phía nó.
-
C.
\({9.10^9}\) V/m, hướng ra xa nó.
-
D.
9000 V/m, hướng về phía nó.
Đáp án : D
Điện tích điểm dương sinh ra điện trường có chiều hướng ra xa nó, điện tích điểm âm sinh ra điện trường có chiều hướng về phía nó.
Áp dụng công thức: \(E = \frac{{k.\left| Q \right|}}{{\varepsilon {r^2}}}\)
Vì điện tích điểm là \( - 1\mu C < 0\) nên điện trường sinh ra có hướng về phía nó.
Độ lớn của cường độ điện trường là:
\(E = \frac{{k.\left| Q \right|}}{{\varepsilon {r^2}}} = \frac{{{{9.10}^9}.\left| { - {{1.10}^{ - 6}}} \right|}}{{{1^2}}} = 9000\) (V/m)
Một điện tích \(1\mu {\rm{C}}\) đặt trong chân không sinh ra điện trường tại một điểm cách nó 1m có độ lớn và hướng là
-
A.
9000V/m, hướng về phía nó.
-
B.
9000V/m, hướng ra xa nó.
-
C.
\({9.10^9}V/m\), hướng về phía nó.
-
D.
\({9.10^9}V/m\), hướng ra xa nó.
Đáp án : B
Điện tích điểm dương sinh ra điện trường có hướng ra xa điện tích, một điện tích điểm âm sinh ra điện trường hướng về phía điện tích
Áp dụng công thức: \(E = \frac{{kQ}}{{{r^2}}}\)
Vì q > 0 nên sinh ra điện trường hướng ra xa nó.
Cường độ điện trường \(E = \frac{{kQ}}{{{r^2}}} = \frac{{{{9.10}^9}{{.1.10}^{ - 6}}}}{{{1^2}}} = 9000{\mkern 1mu} \left( {V/m} \right)\)
Hai tấm kim loại song song, cách nhau 1cm và được nhiễm điện trái dấu nhau. Muốn làm cho điện tích \({\rm{q}} = {5.10^{ - 10}}C\) di chuyển từ tấm này đến tấm kia cần tốn một công \(A = {2.10^{ - 9}}J\). Coi điện trường bên trong khoảng giữa hai tấm kim loại là điện trường đều và có các đường sức điện vuông góc với các tấm. Cường độ điện trường bên trong tấm kim loại đó là
-
A.
E = 40V/m.
-
B.
E = 200V/m.
-
C.
E = 400V/m.
-
D.
E = 2V/m.
Đáp án : C
Áp dụng công thức \(A = qU = qEd\)
Cường độ điện trường bên trong tấm kim loại là:
\(E = \frac{A}{{qd}} = \frac{{{{2.10}^{ - 9}}}}{{{{5.10}^{ - 10}}{{.1.10}^{ - 2}}}} = 400\left( {V/m} \right)\)
Luyện tập và củng cố kiến thức Bài 4. Công của lực điện - Hiệu điện thế Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập công của lực điện - Hiệu điện thế Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6. Tụ điện Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập về tụ điện Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập chuyển động của điện tích trong điện trường Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Ôn tập chương 1 Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3. Điện trường Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập định luật Culông (phần 2) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Tổng hợp bài tập định luật Culông (phần 1) Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2. Thuyết electron và định luật bảo toàn điện tích Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1. Điện tích - Định luật Culông Vật Lí 11 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
