Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học

Bài 8. Một số bài toán thường gặp về đồ thị

Bài 63 trang 57 SGK giải tích 12 nâng cao

a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số: b) Chứng minh rằng đường thẳng luôn đi qua một điểm cố định của đường cong (H) khi m biến thiên. c) Tìm các giá trị của m sao cho đường thẳng đã cho cắt đường cong (H) tại hai điểm thuộc cùng một nhánh của (H).

Lựa chọn câu để xem lời giải nhanh hơn

LG a

Khảo sát sự biến thiên và vẽ đồ thị \((H)\) của hàm số: \(y = {{x + 2} \over {2x + 1}}\)

Lời giải chi tiết:

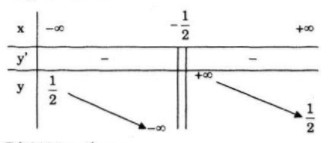
Tập xác định: \(D =\mathbb R\backslash \left\{ { - {1 \over 2}} \right\}\)

+) Sự biến thiên:

\(y' = {{ - 3} \over {{{(2x + 1)}^2}}} < 0\,\forall x \in D\)

Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - {1 \over 2}} \right)\) và \(\left( { - {1 \over 2}; + \infty } \right)\)

Giới hạn:

\(\mathop {\lim y}\limits_{x \to - {{{1 \over 2}}^ - }} = - \infty ;\,\mathop {\lim y}\limits_{x \to - {{{1 \over 2}}^ + }} = + \infty \)

Hầm số không có cực trị.

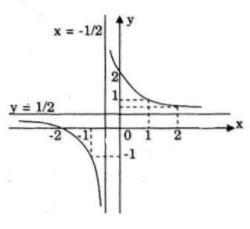
Tiệm cận đứng: \(x={ - {1 \over 2}}\)

\(\mathop {\lim y}\limits_{x \to \pm \infty } = {1 \over 2}\)

Tiệm cận ngang \(y={1 \over 2}\)

Bảng biến thiên:

Đồ thị giao \(Ox\) tại điểm \((-2;0)\)

Đồ thị giao \(Oy\) tại điểm \((0;2)\)

LG b

Chứng minh rằng đường thẳng \(y = mx + m - 1\) luôn đi qua một điểm cố định của đường cong (H) khi m biến thiên.

Lời giải chi tiết:

Ta có \(y = mx + m - 1 \) \(\Leftrightarrow y + 1 = m\left( {x + 1} \right)\)

Tọa độ điểm cố định \(A\) của đường thẳng là nghiệm của hệ:

\(\left\{ \matrix{
x + 1 = 0 \hfill \cr
y + 1 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 1 \hfill \cr
y = - 1 \hfill \cr} \right.\)

Vậy \(A(-1;-1)\)

Thay tọa độ của A vào công thức hàm số ta thấy: \( - 1 = \frac{{ - 1 + 2}}{{2.\left( { - 1} \right) + 1}}\) (đúng) nên \(A\) thuộc đường cong \((H)\).

Cách khác:

Gọi điểm cố định mà đường thẳng y = mx+m-1 luôn đi qua là I.

Ta có \(I\left( {{x_0};\frac{{{x_0} + 2}}{{2{x_0} + 1}}} \right) \in \left( H \right)\) thay vào phương trình y=mx+m-1 được:

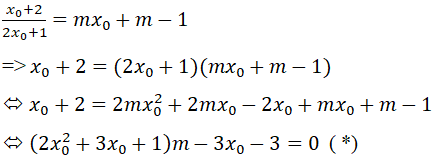
Để phương trình (*) luôn đúng với mọi m khi và chỉ khi:

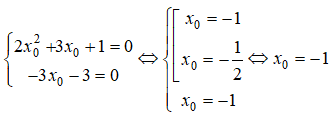
Vậy đường thẳng y=mx+m-1 luôn đi qua 1 điểm cố định I(-1; -1) của đường cong (H) khi m biến thiên.

LG c

Tìm các giá trị của m sao cho đường thẳng đã cho cắt đường cong \((H)\) tại hai điểm thuộc cùng một nhánh của (H).

Lời giải chi tiết:

Hoành độ giao điểm của đường thẳng đã cho và đường cong \((H)\) là nghiệm của phương trình:

\(\eqalign{
& m\left( {x + 1} \right) - 1 = {{x + 2} \over {2x + 1}}\cr & \Leftrightarrow \left( {2x + 1} \right)\left[ {m\left( {x + 1} \right) - 1} \right] = x + 2 \cr
& \Leftrightarrow m\left( {x + 1} \right)\left( {2x + 1} \right) - \left( {2x + 1} \right) = x + 2 \cr
& \Leftrightarrow \left( {x + 1} \right)\left( {2mx + m} \right) - 3x - 3 = 0 \cr&\Leftrightarrow \left( {x + 1} \right)\left( {2mx + m} \right) - 3\left( {x + 1} \right) = 0\cr&\Leftrightarrow \left( {x + 1} \right)\left( {2mx + m - 3} \right) = 0\cr& \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
f\left( x \right) = 2mx + m - 3 = 0\,\,\,\left( 1 \right) \hfill \cr} \right. \cr} \)

Hai nhánh của \((H)\) nằm về hai bên của tiệm cận đứng \(x = - {1 \over 2}\)

Điểm \(A(-1;-1)\) thuộc nhánh trái của \((H)\) vì \({x_A} = - 1 < - {1 \over 2}\)

Đường thẳng cắt \((H)\) tại hai điểm thuộc cùng một nhánh khi và chỉ khi (1) có nghiệm \(x < - {1 \over 2}\) và \(x \ne - 1\) tức

\(\left\{ \matrix{
2m \ne 0 \hfill \cr
x = {{ - m + 3} \over {2m}} < - {1 \over 2} \hfill \cr
f\left( { - 1} \right) \ne 0 \hfill \cr} \right.\) \( \Leftrightarrow \left\{ \matrix{
m \ne 0 \hfill \cr
- {1 \over 2}+{3 \over {2m}} < - {1 \over 2} \hfill \cr
- m - 3 \ne 0 \hfill \cr} \right. \)

\( \Leftrightarrow \left\{ \begin{array}{l}
m \ne 0\\
\frac{3}{{2m}} < 0\\
- m \ne 3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m \ne 0\\
m < 0\\
m \ne - 3
\end{array} \right.\)

\(\Leftrightarrow m < - 3\,\, \text{hoặc}\, - 3 < m < 0.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.1 trên 8 phiếu

Bài tiếp theo

Bài 64 trang 57 SGK giải tích 12 nâng cao
Cho hàm số a)Tìm a và b biết rằng đồ thị (C) của hàm số đã cho đi qua điểm và tiếp tuyến của (C) tại điểm O(0;0) có hệ số bằng -3. b)Khảo sát sự biến thiên và vẽ đồ thị của hàm số với các giá trị của a và b đã tìm được.
Bài 65 trang 58 sách giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: b) Với các giá trị nào t=của m đường thẳng y = m – x cắt đồ thị hàm số đã cho tại hao điểm phân biệt? c) Gọi A và B là hai giao điểm đó. Tìm tập hợp các trung điểm của đoạn thẳng AB khi m biến thiên.
Bài 66 trang 58 SGK giải tích 12 nâng cao
Tìm các hệ số a, b sao cho parabol tiếp xúc với hypebol tại điểm
Bài 67 trang 58 SGK giải tích 12 nâng cao
Giải bài 67 trang 58 sách giáo khoa giải tích 12 nâng cao. Một tạp chí với giá 20 nghìn đồng muột cuốn....
Bài 62 trang 57 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số: b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đường cong đã cho là tâm đối xứng của nó.
Bài 61 trang 56 SGK giải tích 12 nâng cao
Một viên đạn được bắn ra với vận tốc ban đầu từ một nòng súng đặt ở gốc tọa độ O, nghiêng một góc với mặt đất (nòng súng nằm trong mặt phẳng thẳng đứng Oxy và tạo với trục hoành Ox góc ). Biết quỹ đạo chuyển động của viên đạn là parabol.
Bài 60 trang 56 SGK giải tích 12 nâng cao
Chứng minh rằng các đồ thị của hai hàm số: tiếp xúc với nhau. Xác định tiếp điểm của hai đường cong trên và viết phương trình tiếp tuyến chung tại điểm đó.
Bài 59 trang 56 SGK giải tích 12 nâng cao
Chứng minh rằng các đồ thị của ba hàm số: tiếp xúc với nhau tại điểm A(-1;2) (tức là chúng có cùng tiếp tuyến tại A).
Bài 58 trang 56 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: b) Với các giá nào của m, đường thẳng đi qua điểm A(-2;2) và có hệ số góc m cắt đồ thị của hàm số đã cho: •Tại hai điểm phân biệt? •Tại hai điểm thuộc hai nhánh của đồ thị?
Bài 57 trang 55 SGK giải tích 12 nâng cao
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: b) Tìm các giao điểm của đường cong (C) và parabol: c) Viết phương trình các tiếp tuyến của (C) và (P) tại mỗi giao điểm của chúng. d) Xác định các khoảng trên đó (C) nằm phía trên hoặc phía dưới (C).