Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Bài 8. Một số bài toán thường gặp về đồ thị

Bài 57 trang 55 SGK giải tích 12 nâng cao


a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số: b) Tìm các giao điểm của đường cong (C) và parabol: c) Viết phương trình các tiếp tuyến của (C) và (P) tại mỗi giao điểm của chúng. d) Xác định các khoảng trên đó (C) nằm phía trên hoặc phía dưới (C).

Lựa chọn câu để xem lời giải nhanh hơn

LG a

Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số:

\(f\left( x \right) = 2{x^3} + 3{x^2} + 1\)

Lời giải chi tiết:

Tập xác định: \(D=\mathbb R\)

\(f'(x)=6x^2+6x\)

\(f'(x)=0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
x = - 1 \hfill \cr} \right.\)

Bảng biến thiên:

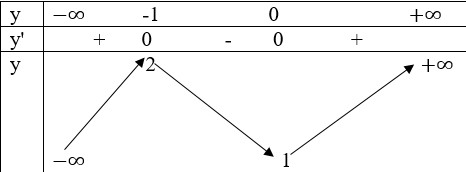
- Hàm số đồng biến trên \(( - \infty ;-1)\) và \((0; + \infty )\)

- Hàm số nghịch biến trên \((-1;0)\)

- Hàm số đạt cực tại \(x=-1;y_{CĐ}=2\)

- Hàm số đạt cực tiểu tại \(x=0;y_{CT}=1\)

\(\mathop {\lim }\limits_{x \to  \pm \infty } y =  \pm \infty \)

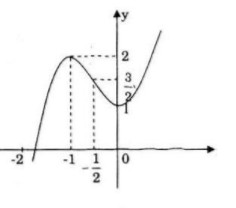
Đồ thị giao trục \(Oy\) tại điểm \((0;1)\), đi qua điểm (-1;2).

Điểm uốn:

Ta có y’’ = 12x + 6

y''=0 <=> 12x+6=0

<=> x=-1/2 => y=3/2

LG b

Tìm các giao điểm của đường cong \((C)\) và parabol:

\((P):\,\,\,g\left( x \right) = 2{x^2} + 1\)

Lời giải chi tiết:

Hoành độ giao điểm của đường cong \((C)\) và paraobol \((P)\) là nghiệm của phương trình:

\(\eqalign{
& \,\,\,\,2{x^3} + 3{x^2} + 1 = 2{x^2} + 1 \cr&\Leftrightarrow 2{x^3} + {x^2} = 0 \cr 
& \Leftrightarrow {x^2}\left( {2x + 1} \right) = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr 
x = - {1 \over 2} \hfill \cr} \right. \cr} \)

Với \(x = 0\) ta có \(y = 1\); với \(x =  - {1 \over 2}\) ta có \(y = {3 \over 2}\)

Ta có giao điểm \(A(0;1)\) và \(B\left( { - {1 \over 2};{3 \over 2}} \right)\)

LG c

Viết phương trình các tiếp tuyến của \((C)\) và \((P)\) tại mỗi giao điểm của chúng.

Lời giải chi tiết:

\(f'\left( x \right) = 6{x^2} + 6x;\,g'\left( x \right) = 4x\)

\(f'\left( 0 \right) = 0;\,g'\left( 0 \right) = 0\).

Đường thẳng \(y = 1\) là tiếp tuyến chung của \((C)\) và \((P)\) tại điểm \(A(0;1)\).

Ta có: \(f'\left( { - {1 \over 2}} \right) =  - {3 \over 2}\).

Phương trình tiếp tuyến của \((C)\) tại điểm \(B\) là: 

\(y =  - {3 \over 2}\left( {x + {1 \over 2}} \right) + {3 \over 2}\) hay \(y =  - {3 \over 2}x + {3 \over 4}\)

Lại có: \(g'\left( { - {1 \over 2}} \right) =  - 2\).

Phương trình tiếp tuyến của parabol \((P)\) tại điểm \(B\) là:

\(y =  - 2\left( {x + {1 \over 2}} \right) + {3 \over 2}\) hay \(y =  - 2x + {1 \over 2}\)

LG d

Xác định các khoảng trên đó \((C)\) nằm phía trên hoặc phía dưới \((C)\).

Lời giải chi tiết:

Xét hiệu \(f\left( x \right) - g\left( x \right)\)

\(= 2{x^3} + 3{x^2} + 1 - 2{x^2} - 1 \)

\(= 2{x^3} + {x^2} = {x^2}\left( {2x + 1} \right)\)

Xét dấu \(f\left( x \right) - g\left( x \right)\):

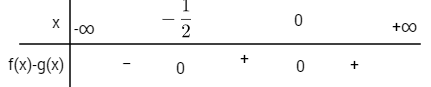
Do đó \(f\left( x \right) - g\left( x \right) < 0 \Leftrightarrow x <  - \frac{1}{2}\) nên trên khoảng \(\left( { - \infty ; - {1 \over 2}} \right)\) thì \((C)\) nằm phía dưới \((P)\)

\(f\left( x \right) - g\left( x \right) > 0 \Leftrightarrow \left\{ \begin{array}{l}
x > - \frac{1}{2}\\
x \ne 0
\end{array} \right.\) thì \(f(x) > g(x)\) hay đồ thị (C) nằm phía trên (P) trên các khoảng \(\left( { - {1 \over 2};0} \right)\) và \(\left( {0; + \infty } \right)\).

Loigiaihay.com


Bình chọn:
3.9 trên 9 phiếu
Bài tiếp theo
  • Bài 58 trang 56 SGK giải tích 12 nâng cao

    a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: b) Với các giá nào của m, đường thẳng đi qua điểm A(-2;2) và có hệ số góc m cắt đồ thị của hàm số đã cho: •Tại hai điểm phân biệt? •Tại hai điểm thuộc hai nhánh của đồ thị?

  • Bài 59 trang 56 SGK giải tích 12 nâng cao

    Chứng minh rằng các đồ thị của ba hàm số: tiếp xúc với nhau tại điểm A(-1;2) (tức là chúng có cùng tiếp tuyến tại A).

  • Bài 60 trang 56 SGK giải tích 12 nâng cao

    Chứng minh rằng các đồ thị của hai hàm số: tiếp xúc với nhau. Xác định tiếp điểm của hai đường cong trên và viết phương trình tiếp tuyến chung tại điểm đó.

  • Bài 61 trang 56 SGK giải tích 12 nâng cao

    Một viên đạn được bắn ra với vận tốc ban đầu từ một nòng súng đặt ở gốc tọa độ O, nghiêng một góc với mặt đất (nòng súng nằm trong mặt phẳng thẳng đứng Oxy và tạo với trục hoành Ox góc ). Biết quỹ đạo chuyển động của viên đạn là parabol.

  • Bài 62 trang 57 SGK giải tích 12 nâng cao

    a) Khảo sát sự biến thiên và vẽ đồ thị hàm số: b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đường cong đã cho là tâm đối xứng của nó.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store