-
ĐẠI SỐ - SBT TOÁN 10 NÂNG CAO
-
Chương 1: Mệnh đề - Tập hợp
-
Chương 2: Hàm số
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT VÀ BẬC HAI
- Bài 1. Đại cương về phương trình
- Bài 2. Phương trình bậc nhất và bậc hai một ẩn
- Bài 3. Một số phương trình quy về phương trình bậc nhất hoặc bậc hai
- Bài 4. Phương trình và hệ phương trình bậc nhất nhiều ẩn
- Bài 5. Một số ví dụ về hệ phương trình bậc hai hai ẩn
- Bài tập Ôn tập chương III - Phương trình bậc nhất và bậc hai
-
CHƯƠNG IV. BẤT ĐẲNG THỨC VÀ BẤT PHƯƠNG TRÌNH
- Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
- Bài 2. Đại cương về bất phương trình
- Bài 3. Bất phương trình và hệ bất phương trình bậc nhất một ẩn
- Bài 4. Dấu của nhị thức bậc nhất
- Bài 5. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
- Bài 6. Dấu của tam thức bậc hai
- Bài 7. Bất phương trình bậc hai
- Bài 8. Một số phương trình và bất phương trình quy về bậc hai
- Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
-
CHƯƠNG V. THỐNG KÊ
-
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
-
BÀI TẬP ÔN TẬP CUỐI NĂM - ĐẠI SỐ 10 NÂNG CAO
-
-
HÌNH HỌC-SBT TOÁN 10 NÂNG CAO
Bài 62 trang 111 SBT Hình học 10 Nâng cao
Giải bài tập Bài 62 trang 111 SBT Hình học 10 Nâng cao
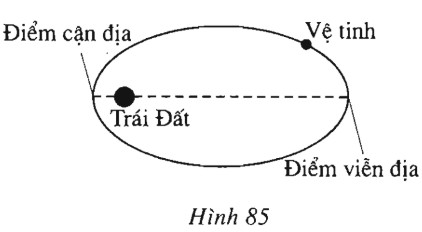
Mặt trăng và các vệ tinh của Trái Đất chuyển động theo quỹ đạo là các đường elip mà tâm Trái Đất là một tiêu điểm. Điểm gần Trái Đất nhất trên quỹ đạo gọi là điểm cận địa, điểm xa Trái Đất nhất trên quỹ đạo gọi là điểm viễn địa (h.85).
LG a
Biết khoảng cách từ điểm viễn địa đến điểm cận địa trên quỹ đạo của một vệ tinh đến tâm Trái Đất thứ tự là m và n. Chứng minh rằng tâm sai của quỹ đạo này bằng \( \dfrac{{m - n}}{{m + n}}\).
Lời giải chi tiết:
\(m = a + c, n = a - c \)
\( \Rightarrow \dfrac{{m - n}}{{m + n}} = \dfrac{{(a + c) - (a - c)}}{{a + c + a - c}} \)
\(= \dfrac{{2c}}{{2a}} = e\).
LG b
Biết độ dài trục lớn và độ dài trục bé của quỹ đạo Mặt Trăng là \(768806\) km và \(767746\) km. Tính khoảng cách lớn nhất và khoảng cách bé nhất giữa tâm Trái Đất và tâm của Mặt Trăng.
Lời giải chi tiết:
\(\begin{array}{l}2a = 768806 \Rightarrow a = 384403 ; \\ 2b = 767746 \Rightarrow b = 383873 ;\\c = \sqrt {{a^2} - {b^2}} \approx 20179.\end{array}\)
Vậy khoảng cách lớn nhất từ tâm Trái Đất tới tâm Mặt Trăng là:
\(a + c \approx 404582\) (km) và khoảng cách bé nhất là : \(a - c \approx 364224\) (km).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 63 trang 111 SBT Hình học 10 Nâng cao
- Bài 64 trang 111 SBt Hình học 10 Nâng cao
- Bài 65 trang 112 SBT Hình học 10 Nâng cao
- Bài 66 trang 112 SBT Hình học 10 Nâng cao
- Bài 67 trang 112 SBT Hình học 10 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
2k8 Tham gia ngay group chia sẻ, trao đổi tài liệu học tập miễn phí
>> Học trực tuyến Lớp 10 tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
