Giải SBT toán hình học và đại số 10 nâng cao Bài 5. Đường elip.

Bài 59 trang 110 SBT Hình học 10 Nâng cao


Giải bài tập Bài 59 trang 110 SBT Hình học 10 Nâng cao

Đề bài

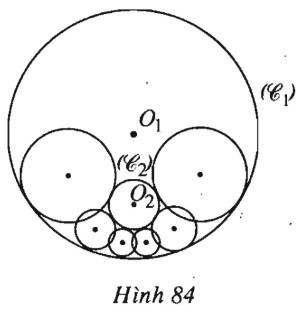
Cho đường tròn \((C_1)\) tâm \(O_1\), bán kính \(R_1\) và đường tròn \((C_2)\) tâm \(O_2\), bán kính \(R_2\). Biết  đường tròn \((C_2)\) nằm trong đường tròn \((C_1)\) và tâm hai đường tròn không trùng nhau (h.84). Tìm tập hợp tâm của các đường tròn tiếp xúc ngoài với \((C_2)\) và tiếp xúc trong với \((C_1)\).

Lời giải chi tiết

(h.109).

 

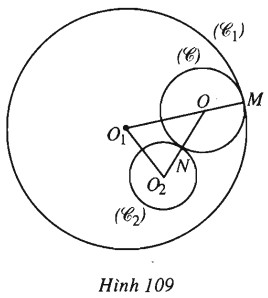
Xét đường tròn \((C)\) tâm \(O\), tiếp xúc trong với \((C_1)\) tại \(M\), tiếp xúc ngoài với \((C_2)\) tại \(N\). Ta có:

\(O{O_1} + O{O_2}\)

\(= {O_1}M - OM + {O_2}N + ON \)

\(= {R_1} + {R_2}\) không đổi.

Tập hợp các tâm \(O\) là elip có các tiêu điểm là \(O_1, O_2\) và độ dài trục lớn \(2a=R_1+R_2\).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store