Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Bài 8. Một số bài toán thường gặp về đồ thị

Bài 60 trang 56 SGK giải tích 12 nâng cao


Chứng minh rằng các đồ thị của hai hàm số: tiếp xúc với nhau. Xác định tiếp điểm của hai đường cong trên và viết phương trình tiếp tuyến chung tại điểm đó.

Đề bài

Chứng minh rằng các đồ thị của hai hàm số: \(f\left( x \right) = {{{x^2}} \over 2} + {3 \over 2}x\) và \(g\left( x \right) = {{3x} \over {x + 2}}\) tiếp xúc với nhau. Xác định tiếp điểm của hai đường cong trên và viết phương trình tiếp tuyến chung tại điểm đó.

Phương pháp giải - Xem chi tiết

Hai đường cong f(x) và g(x) tiếp xúc nhau nếu hệ sau có nghiệm: 

\(\left\{ \begin{array}{l}
f\left( x \right) = g\left( x \right)\\
f'\left( x \right) = g'\left( x \right)
\end{array} \right.\)

Nghiệm của hệ trên chính là hoành độ tiếp điểm.

Lời giải chi tiết

Hoành độ tiếp điểm của hai đường cong đã cho là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}
f\left( x \right) = g\left( x \right)\\
f'\left( x \right) = g'\left( x \right)
\end{array} \right.\)

\(\eqalign{
\Leftrightarrow  & \left\{ \matrix{
{{{x^2}} \over 2} + {3 \over 2}x = {{3x} \over {x + 2}} \hfill \cr 
{\left( {{{{x^2}} \over 2} + {3 \over 2}x} \right)'} = {\left( {{{3x} \over {x + 2}}} \right)'} \hfill \cr} \right. \cr&\Leftrightarrow \left\{ \matrix{
{{{x^2}} \over 2} + {3 \over 2}x = {{3x} \over {x + 2}}\,(1) \hfill \cr 
x + {3 \over 2} = {6 \over {{{\left( {x + 2} \right)}^2}}}\,(2) \hfill \cr} \right. \cr } \)

\(\begin{array}{l}
\left( 1 \right) \Leftrightarrow \frac{{{x^2} + 3x}}{2} = \frac{{3x}}{{x + 2}}\\
\Leftrightarrow \frac{{{x^2} + 3x}}{2} - \frac{{3x}}{{x + 2}} = 0\\
\Leftrightarrow \frac{{\left( {{x^2} + 3x} \right)\left( {x + 2} \right) - 6x}}{{2\left( {x + 2} \right)}} = 0\\
\Rightarrow \left( {{x^2} + 3x} \right)\left( {x + 2} \right) - 6x = 0\\
\Leftrightarrow {x^3} + 3{x^2} + 2{x^2} + 6x - 6x = 0\\
\Leftrightarrow {x^3} + 5{x^2} = 0\\
\Leftrightarrow {x^2}\left( {x + 5} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
{x^2} = 0\\
x + 5 = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = - 5
\end{array} \right.\left( {TM} \right)
\end{array}\)

Thay x=0 và x=-5 vào (2) ta được:

+) \(x=0\) thì \(VT=0 + \frac{3}{2} = \frac{3}{2} = \frac{6}{{{{\left( {0 + 2} \right)}^2}}}=VP\) nên x=0 thỏa mãn (2)

Do đó x=0 là nghiệm của hệ.
+) \(x =-5\) thì \(VT =  - 5 + \frac{3}{2} =  - \frac{7}{2} \ne \frac{6}{{{{\left( { - 5 + 2} \right)}^2}}} = VP\) nên x=-5 không thỏa mãn (2)

Vậy hệ có \(1\) nghiệm duy nhất \(x = 0\) suy ra y=0.

Vậy hai đường cong tiếp xúc với nhau tại gôc tọa độ \(O\); \(y'\left( 0 \right) = {3 \over 2}\).

Phương trình tiếp tuyến chung của hai đường cong tại điểm gốc là \(y = {3 \over 2}x.\)

Cách khác:

Các em có thể giải trực tiếp hệ trên mà không cần thay như sau:

Loigiaihay.com


Bình chọn:
3.7 trên 6 phiếu
Bài tiếp theo
  • Bài 61 trang 56 SGK giải tích 12 nâng cao

    Một viên đạn được bắn ra với vận tốc ban đầu từ một nòng súng đặt ở gốc tọa độ O, nghiêng một góc với mặt đất (nòng súng nằm trong mặt phẳng thẳng đứng Oxy và tạo với trục hoành Ox góc ). Biết quỹ đạo chuyển động của viên đạn là parabol.

  • Bài 62 trang 57 SGK giải tích 12 nâng cao

    a) Khảo sát sự biến thiên và vẽ đồ thị hàm số: b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đường cong đã cho là tâm đối xứng của nó.

  • Bài 63 trang 57 SGK giải tích 12 nâng cao

    a) Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số: b) Chứng minh rằng đường thẳng luôn đi qua một điểm cố định của đường cong (H) khi m biến thiên. c) Tìm các giá trị của m sao cho đường thẳng đã cho cắt đường cong (H) tại hai điểm thuộc cùng một nhánh của (H).

  • Bài 64 trang 57 SGK giải tích 12 nâng cao

    Cho hàm số a)Tìm a và b biết rằng đồ thị (C) của hàm số đã cho đi qua điểm và tiếp tuyến của (C) tại điểm O(0;0) có hệ số bằng -3. b)Khảo sát sự biến thiên và vẽ đồ thị của hàm số với các giá trị của a và b đã tìm được.

  • Bài 65 trang 58 sách giải tích 12 nâng cao

    a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: b) Với các giá trị nào t=của m đường thẳng y = m – x cắt đồ thị hàm số đã cho tại hao điểm phân biệt? c) Gọi A và B là hai giao điểm đó. Tìm tập hợp các trung điểm của đoạn thẳng AB khi m biến thiên.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

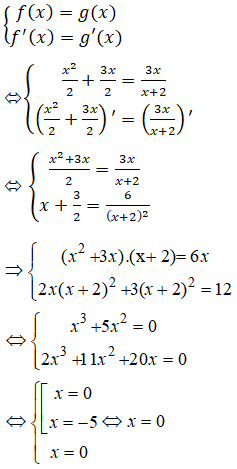
Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store