Bài 54 trang 216 SGK Đại số 10 Nâng cao

Tính tầm xa theo α (và v)

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

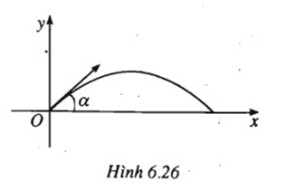
Quỹ đạo của một vật được ném lên từ gốc O, với vận tốc ban đầu là v(m/s) theo phương hợp với trục hoành (nằm ngang) Ox một góc α , $0 < \alpha < {\pi \over 2}$ là parabol có phương trình :

$y = - {g \over {2{v^2}{{\cos }^2}\alpha }}{x^2} + (\tan \alpha )x$

Trong đó g là gia tốc trọng trường (g ≈ 9,8m/s²) (giả sử lực cản của không khí là không đáng kể).

Gọi tầm xa của quỹ đạo là khoảng cách từ O đến giao điểm khác O của quỹ đạo với Ox.

LG a

Tính tầm xa theo α (và v)

Lời giải chi tiết:

Gọi x là tầm xa của quỹ đạo, thì:

$\left\{ \matrix{ x > 0 \hfill \cr - {{g{x^2}} \over {2{v^2}{{\cos }^2}\alpha }} + (\tan \alpha )x = 0 \hfill \cr} \right.$

$\begin{array}{l} \Leftrightarrow - \frac{{gx}}{{2{v^2}{{\cos }^2}\alpha }} + \tan \alpha = 0\\ \Leftrightarrow - \frac{{gx}}{{2{v^2}{{\cos }^2}\alpha }} = - \tan \alpha \\ \Leftrightarrow gx = 2{v^2}{\cos ^2}\alpha \tan \alpha \\ \Leftrightarrow x = \frac{{2{v^2}{{\cos }^2}\alpha \tan \alpha }}{g}\\ \Leftrightarrow x = \frac{{2{v^2}{{\cos }^2}\alpha .\frac{{\sin \alpha }}{{\cos \alpha }}}}{g}\\ \Leftrightarrow x = \frac{{2{v^2}\cos \alpha \sin \alpha }}{g}\\ \Leftrightarrow x = \frac{{{v^2}\sin 2\alpha }}{g} \end{array}$

LG b

Khi v không đổi, α thay đổi trong khoảng $(0,\,{\pi \over 2})$ , hỏi giá trị α nào thì tầm xa của quỹ đạo đạt được giá trị lớn nhất? Tính giá trị đó theo v. Khi v = 80m/s. Hãy tính giá trị lớn nhất đó (chính xác đến hàng đơn vị).

Lời giải chi tiết:

x đạt giá trị lớn nhất khi và chỉ khi $\sin 2\alpha = 1 \Rightarrow \alpha = {\pi \over 4}$

Khi đó: $x = {{{v^2}} \over g}$

Với $v = 80m/s$ thì $x={{{v^2}} \over g} \approx {{{{80}^2}} \over {9,8}} \approx 653(m)$

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.5 trên 2 phiếu

Bài tiếp theo

Bài 53 trang 216 SGK Đại số 10 Nâng cao
Hãy tính sin(α + β ) theo a và b
Bài 52 trang 216 SGK Đại số 10 Nâng cao
Chứng minh rằng với mọi ∝ mà cos k∝ ≠ 0 (k = 1, 2, 3, 4, 5, 6, 7, 8) và sin ∝ ≠ 0 thì:
Bài 51 trang 216 SGK Đại số 10 Nâng cao
Chứng minh rằng nếu ∝ + β + γ = π thì
Bài 50 trang 215 SGK Đại số 10 Nâng cao
Chứng minh rằng nếu tam giác ABC có 3 góc thỏa:
Bài 49 trang 215 SGK Đại số 10 Nâng cao
Chứng minh rằng giá trị của mỗi biểu thức sau không phụ thuộc vào x
Bài 48 trang 215 SGK Đại số 10 Nâng cao
Chứng minh rằng:
Bài 47 trang 215 SGK Đại số 10 Nâng cao
Chứng minh rồi dùng máy tính bỏ túi hoặc bảng số để kiểm nghiệm lại gần đúng kết quả.
Bài 46 trang 215 SGK Đại số 10 Nâng cao
Chứng minh rằng:
Bài 45 trang 214 SGK Đại số 10 Nâng cao
Chứng minh rằng:
Bài 44 trang 214 SGK Đại số 10 Nâng cao
Đơn giản các biểu thức sau:
Bài 43 trang 214 SGK Đại số 10 Nâng cao
Dùng công thức biến đổi tích thành tổng, chứng minh:
Bài 42 trang 214 SGK Đại số 10 Nâng cao
Chứng minh rằng:
Bài 41 trang 214 SGK Đại số 10 Nâng cao
Hãy tính giá trị lượng giác sau:
Bài 40 trang 213 SGK Đại số 10 Nâng cao
Chứng minh rằng:
Bài 39 trang 213 SGK Đại số 10 Nâng cao
Sử dụng 750 = 450 + 30o, hãy tính giá trị lượng giác của góc 750
Bài 38 trang 213 SGK Đại số 10 Nâng cao
Hỏi mỗi khẳng định sau đây có đúng không? ∀α,∀β ta có:

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Click để xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.