Bài 4 trang 122 SGK Hình học 12 Nâng cao

Chứng minh rằng trung điểm các cạnh của một hình tứ diện đều là các đỉnh của một hình tám mặt đều. Hãy so sánh thể tích của tứ diện đều đã cho và thể tích của hình tám mặt đều đó.

Đề bài

Chứng minh rằng trung điểm các cạnh của một hình tứ diện đều là các đỉnh của một hình tám mặt đều. Hãy so sánh thể tích của tứ diện đều đã cho và thể tích của hình tám mặt đều đó.

Lời giải chi tiết

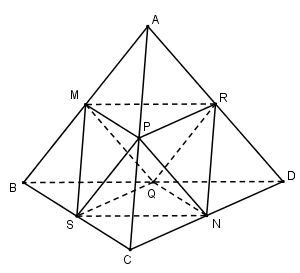
Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, CD, AC, BD, AD, BC của tứ diện đều ABCD thì các tam giác MPR, MRQ, MQS, MSP, NPR, NRQ, NQS, NSP là những tam giác đều, vậy ta có hình tám mặt đều MPNQRS.

Vì các tứ diện AMPR, BMQS, CPSN, DQNR đều là những tứ diện đồng dạng với tứ diện ABCD với tỉ số \(k = {1 \over 2}\) nên ta có thể tích bằng \({V \over 8}.\)

Suy ra \({V_{MPRQSN}} = V - 4{V \over 8} = {V \over 2}.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.5 trên 4 phiếu

Bài tiếp theo

Bài 5 trang 122 SGK Hình học 12 Nâng cao
Cho hình vuông ABCD nội tiếp đường tròn (O; R). Gọi H là hình gồm các điểm của hình tròn (O; R) nhưng không nằm trong hình vuông. Tính thể tích hình tròn xoay sinh bởi hình H khi quay quanh đường thẳng chứa một đường chéo của hình vuông.
Bài 6 trang 123 SGK Hình học 12 Nâng cao
Cho hình lục giác đều ABCDEF cạnh a. a) Tính thể tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng AD. b) Tính thế tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng đi qua trung điểm của các cạnh AB và DE.
Bài 7 trang 123 SGK Hình học 12 Nâng cao
Cho hình trụ có bán kính R và đường cao . Gọi AB và CD là hai đường kính thay đổi của hai đường tròn đáy mà AB vuông góc với CD. a) Chứng minh ABCD là tứ diện đều. b) Chứng minh rằng các đường thẳng AC, AD, BC, BD luôn tiếp xúc với một mặt trụ cố định (tức là khoảng cách giữa mỗi đường thẳng đó và trục của mặt trụ bằng bán kính mặt trụ).
Bài 8 trang 123 SGK Hình học 12 Nâng cao
Trong không gian tọa độ Oxyz cho các điểm A(1; 5; 3), B(4; 2; -5), C(5; 5; -1) và D(1; 2; 4). a) Chứng tỏ rằng bốn điểm A, B, C, D không đồng phẳng. b) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D . Xác định tâm và bán kính của mặt cầu đó. c) Viết phương trình mặt phẳng đi qua A, B, C và tìm khoảng cách từu điểm D tới mặt phẳng đó. d) Viết phương trình mặt phẳng vuông góc với CD và tiếp xúc với mặt cầu (S). e) Tìm bán kính các đường tròn giao tuyến của mặt cầu (S) và các mặt phẳ
Bài 9 trang 123 SGK Hình học 12 Nâng cao
Trong không gian tọa độ Oxyz cho đường thẳng có phương trình a) Viết phương trình hình chiếu của trên các mặt phẳng tọa độ. b) Chứng minh rằng mặt phẳng đi qua đường thẳng . c) Tính khoảng cách giữa đường thẳng và các trục tọa độ. d) Viết phương trình đường vuông góc chung của hai đường thẳng và e) Viết phương trình đường thẳng song song với Oz, cắt cả và ’.
Bài 10 trang 124 SGK Hình học 12 Nâng cao
Trong không gian tọa độ Oxyz, cho hai điểm A(1; -1; 2), B(2; 0; 1). a) Tìm quỹ tích các điểm M sao cho b) Tìm quỹ tích các điểm N sao cho c) Tìm quỹ tích các điểm cách đều hai mặt phẳng (OAB) và (Oxy).
Bài 11 trang 124 SGK Hình học 12 Nâng cao
Trong không gian Oxyz, cho đường thẳng có phương trình trong đó a, b, c thay đổi sao cho a) Chứng minh rằng đường thẳng đi qua một điểm cố định, góc giữa và Oz là không đổi. b) Tìm quỹ tích các giao điểm của và mp(Oxy).
Bài 12 trang 124 SGK Hình học 12 Nâng cao
Cho hình hộp chữ nhật ABCD.A’B’C’D’ với AB = a, BC = b, CC’ = c. a) Tính khoảng cách từ điểm A tới mp(A’BD). b) Tính khoảng cách từ điểm A’ tới đường thẳng C’D. c) Tính khoảng cách giữa hai đường thẳng BC’ và CD’.
Bài 3 trang 122 SGK Hình học 12 Nâng cao
Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Hãy tính thể tích của tứ diện ACB’D’.
Bài 2 trang 122 SGK Hình học 12 Nâng cao
Cho tứ diện ABCD có thể tích V. Hãy tính thể tích hình tứ diện có đỉnh là trọng tâm các mặt của tứ diện đã cho.
Bài 1 trang 122 SGK Hình học 12 Nâng cao
Cho hình lăng trụ ABC.A’B’C’ với cạnh bên không vuông góc với mặt đáy. Gọi là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và cắt chúng tại P, Q, R. Phép tịnh tiến theo vectơ biến tam giác PQR thành tam giác P’Q’R’. a) Chứng minh rằng thể tích V của hình lăng trụ đã cho bằng thể tích của hình lăng trụ PQR.P’Q’R’. b) Chứng minh rằng , trong đó là diện tích tam giác PQR.