Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 28 trang 24 SGK Đại số và Giải tích 12 Nâng cao


Trong các hình chữ nhật có chu vi là 40cm, hãy xác định hình chữ nhật có diện tích lớn nhất.

Đề bài

Trong các hình chữ nhật có chu vi là \(40cm\), hãy xác định hình chữ nhật có diện tích lớn nhất.

Lời giải chi tiết

Nửa chu vi hcn là 40:2=20 (cm)

Gọi \(x (cm)\) là độ dài một cạnh của hình chữ nhật thì cạnh kia có độ dài \(20 – x (cm)\).

Điều kiện: \(0<x<20\)

Diện tích hình chữ nhật là \(S\left( x \right) = x\left( {20 - x} \right) = 20x - {x^2}\) với \(x \in \left( {0;20} \right)\)

Ta có \(S'\left( x \right) = 20 - 2x;\)

\(S'\left( x \right) = 0 \Leftrightarrow x = 10\)

\(S\left( {10} \right) = 100\)

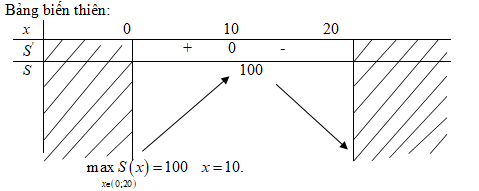
Vậy hình chữ nhật có diện tích lớn nhất khi nó là hình vuông có cạnh dài \(10 cm\).

Cách 2. Sử dụng bất đẳng thức cô – si.

Gọi a, b là hai cạnh của hình chữ nhật, ta có a + b = 20 (a, b >0)

\(\begin{array}{l}a + b \ge 2\sqrt {ab}  \Rightarrow \sqrt {ab}  \le \frac{{a + b}}{2}\\ \Rightarrow ab \le {\left( {\frac{{a + b}}{2}} \right)^2} = {\left( {\frac{{20}}{2}} \right)^2} = 100\end{array}\)

\( \Rightarrow \max \left( {ab} \right) = 100\) đạt được khi \(a = b = 10\).

Vậy hình vuông có cạnh 10 cm là diện tích lớn nhất (trong tất cả các hình chữ nhật có chu vi 40 cm)

Loigiaihay.com


Bình chọn:
3.3 trên 3 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store