Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 25 trang 23 SGK Đại số và Giải tích 12 Nâng cao


Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc bơi của con cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của con cá trong t giờ được cho bởi công thức, trong đó c là một hằng số, E được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.

Đề bài

Một con cá hồi bơi ngược dòng để vượt một khoảng cách là \(300km\). Vận tốc dòng nước là \(6 km/h\). Nếu vận tốc bơi của con cá khi nước đứng yên là \(v (km/h)\) thì năng lượng tiêu hao của con cá trong \(t\) giờ được cho bởi công thức \(E\left( v \right) = c{v^3}t\), trong đó \(c\) là một hằng số, \(E\) được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.

Lời giải chi tiết

Vận tốc của cá hồi khi bơi ngược là \(v – 6 (km/h)\).

Thời gian cá bơi để vượt khoảng cách \(300 km\) là: \(t = {{300} \over {v- 6}}\,\,\left( h \right)\)

Năng lượng tiêu hao của cá để vượt khoảng cách đó là: \(E\left( v \right) = c{v^3}.{{300} \over {v - 6}} = 300c.{{{v^3}} \over {v - 6}}\) (jun) với \(v>6\).

Đạo hàm \(E'\left( v \right) = 300c.{{3{v^2}\left( {v - 6} \right) - {v^3}} \over {{{\left( {v - 6} \right)}^2}}}\) \( = 300c.{{2{v^3} - 18v} \over {{{\left( {v - 6} \right)}^2}}} = 600c.{{{v^2}\left( {v - 9} \right)} \over {{{\left( {v - 6} \right)}^2}}}\)

\(E'\left( v \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
v = 0 \notin \left( {6; + \infty } \right)\\
v = 9 \in \left( {6; + \infty } \right)
\end{array} \right.\)

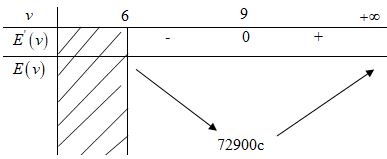
\(E\left( 9 \right) = 72900c\)

Bảng biến thiên:

Để ít tiêu hao năng lượng nhất, cá phải bơi với vận tốc ( khi nước đứng yên) là \(9 (km/h)\).

Loigiaihay.com


Bình chọn:
4 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store