Bài 24 trang 23 sách Đại số và Giải tích 12 Nâng cao

Cho parabol (P): y = x2 và điểm A (-3;0). Xác định điểm M thuộc parabol (P) sao cho khoảng cách AM là ngắn nhất và tìm khoảng cách ngắn nhất đó.

Đề bài

Cho parabol \((P): y = x^2\) và điểm \(A (-3;0)\). Xác định điểm \(M\) thuộc parabol \((P)\) sao cho khoảng cách \(AM\) là ngắn nhất và tìm khoảng cách ngắn nhất đó.

Lời giải chi tiết

Gọi \(M\left( {x;{x^2}} \right)\)

Ta có: \(A{M^2} = {(x + 3)^2} + {x^4} = {x^4} + {x^2} + 6x + 9\)

\(AM\) đạt giá trị nhỏ nhất khi và chỉ khi \(f(x) = {x^4} + {x^2} + 6x + 9\) đạt giá trị nhỏ nhất

Ta có: \(f'(x) = 4{x^3} + 2x + 6 = 2(x + 1)(2{x^2} - 2x + 3)\)

\(f'\left( x \right) = 0 \Leftrightarrow x = - 1;f\left( { - 1} \right) = 5\)

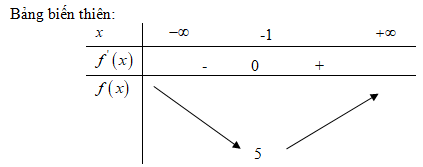
\(f\) đạt giá trị nhỏ nhất tại điểm \(x = -1\), giá trị nhỏ nhất là \(f (-1) = 5\).

\(AM\) đạt giá trị nhỏ nhất khi \(M\) ở vị trí \({M_0} (-1; 1)\) khi đó \(AM_0=\sqrt 5\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 7 phiếu

Bài tiếp theo

Bài 25 trang 23 SGK Đại số và Giải tích 12 Nâng cao
Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 300km. Vận tốc dòng nước là 6 km/h. Nếu vận tốc bơi của con cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của con cá trong t giờ được cho bởi công thức, trong đó c là một hằng số, E được tính bằng jun. Tìm vận tốc bơi của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
Bài 26 trang 23 SGK Đại số và Giải tích 12 Nâng cao
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là Nếu coi f là hàm số xác định trên đoạn thì được xem là tốc độ truyền bệnh( người/ngày) tại thời điểm t. a) Tính tốc độ truyền bệnh vào ngày thứ 5; b) Xác định ngày mà tốc độ truyền bệnh là lớn nhất và tính tốc độ đó; c) Xác định các ngày mà tốc độ truyền bệnh lớn hơn 600; d) Xét chiều biến thiên của hàm số f trên đoạn
Bài 27 trang 24 SGK Đại số và Giải tích 12 Nâng cao
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
Bài 28 trang 24 SGK Đại số và Giải tích 12 Nâng cao
Trong các hình chữ nhật có chu vi là 40cm, hãy xác định hình chữ nhật có diện tích lớn nhất.
Bài 23 trang 23 SGK Đại số và Giải tích 12 Nâng cao
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức:
Bài 22 trang 23 SGK Đại số và Giải tích 12 Nâng cao
Tìm giá trị của m để hàm số có cực đại và cực tiểu.
Bài 21 trang 22 SGK Đại số và Giải tích 12 Nâng cao
Tìm cực trị của các hàm số sau:
Bài 20 trang 22, SGK Đại số và Giải tích 12 Nâng cao
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng: P(n)=480 – 20n. Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.
Bài 19 trang 22 SGK Đại số và Giải tích 12 Nâng cao
Cho một tam giác đều ABC cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định vị trí của điểm M sao cho hình chữ nhật có diện tích lớn nhất và tìm giá trị lớn nhất đó.
Bài 18 trang 22 SGK Đại số và Giải tích 12 Nâng cao
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
Bài 17 trang 22 SGK Đại số và Giải tích 12 Nâng cao
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
Bài 16 trang 22 SGK Đại số và Giải tích 12 Nâng cao
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: