Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 27 trang 24 SGK Đại số và Giải tích 12 Nâng cao


Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

Lựa chọn câu để xem lời giải nhanh hơn

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

LG a

\(f\left( x \right) = \sqrt {3 - 2x} \) trên đoạn \(\left[ { - 3;1} \right]\);

Lời giải chi tiết:

\(f'\left( x \right) = {{ - 1} \over {\sqrt {3 - 2x\,} }} < 0\) với mọi \(x < {3 \over 2}\,\)

Hàm số \(f\) nghịch biến trên đoạn \(\left[ { - 3;1} \right]\)

Do đó \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 3;1} \right]}  = f\left( { - 3} \right) = 3\); \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 3;1} \right]}  = f\left( 1 \right) = 1\)

Cách khác:

\(f'\left( x \right) = {{ - 1} \over {\sqrt {3 - 2x\,} }} = 0\) vô nghiệm trên đoạn [-3;1] 

Mà \(f\left( { - 3} \right) = 3\); \(f\left( 1 \right) = 1\).

Do đó \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 3;1} \right]}  = f\left( { - 3} \right) = 3\); \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 3;1} \right]}  = f\left( 1 \right) = 1\)

LG b

\(f\left( x \right) = x + \sqrt {4 - {x^2}} \)

Lời giải chi tiết:

TXĐ: \(D = \left[ { - 2;2} \right]\)

\(f'\left( x \right) = 1 - {x \over {\sqrt {4 - {x^2}}}}\) với \(x \in \left( { - 2;2} \right)\)

\(f'\left( x \right) = 0 \Leftrightarrow 1 - {x \over {\sqrt {4 - {x^2}}} } = 0 \) \(\Leftrightarrow \sqrt {4 - {x^2}} = x \Leftrightarrow \left\{ \matrix{
0 < x < 2 \hfill \cr 
4 - {x^2} = {x^2} \hfill \cr} \right. \) \(\Leftrightarrow x = \sqrt 2 \)

Ta có \(f\left( { - 2} \right) =  - 2;f\left( {\sqrt 2 } \right) = 2\sqrt 2 ;\) \(f\left( 2 \right) = 2\)

Vậy \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 2;2} \right]}  = 2\sqrt 2 ;\) \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 2;2} \right]}  =  - 2\)

Cách khác:

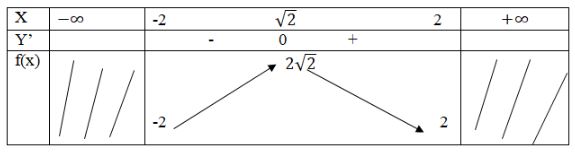
BBT:

Vậy \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - 2;2} \right]}  = 2\sqrt 2 ;\) \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - 2;2} \right]}  =  - 2\)

LG c

\(f\left( x \right) = {\sin ^4}x + {\cos ^2}x + 2;\) 

Lời giải chi tiết:

TXĐ: \(D =\mathbb R\)

Ta có: \(f\left( x \right) = {\sin ^4}x + 1 - {\sin ^2}x + 2 \) \(= {\sin ^4}x - {\sin ^2}x + 3\)

Đặt \(t = {\sin ^2}x;0 \le t \le 1\)

Tìm giá trị nhỏ nhất, lớn nhất của hàm số \(g\left( t \right) = {t^2} - t + 3\) trên đoạn \(\left[ {0;1} \right]\)

\(g'\left( t \right) = 2t - 1\)

\(g'\left( t \right) = 0 \Leftrightarrow t = {1 \over 2}\)

Ta có: \(g\left( 0 \right) = 3;g\left( {{1 \over 2}} \right) = {{11} \over {14}};g\left( 1 \right) = 3\)

Do đó:  \(\mathop {\min g\left( t \right)}\limits_{t \in \left[ {0;1} \right]}  = {{11} \over {14}};\mathop {\max g\left( t \right)}\limits_{t \in \left[ {0;1} \right]}  = 3\)

Vậy: \(\mathop {\min f\left( x \right)}\limits_{x \in {\mathbb{R}}}  = {{11} \over {14}}\) đạt được khi \({\sin ^2}x = \frac{1}{2} \) \(\Leftrightarrow \frac{{1 - \cos 2x}}{2} = \frac{1}{2}  \) \(\Leftrightarrow 1 - \cos 2x = 1 \) \( \Leftrightarrow \cos 2x = 0  \) \(\Leftrightarrow 2x = \frac{\pi }{2} + k\pi  \) \(  \Leftrightarrow x = \frac{\pi }{4} + \frac{{k\pi }}{2}\)

\(\mathop {\max f\left( x \right)}\limits_{x \in {\mathbb{R}}}  = 3\) đạt được khi \( x = \frac{k\pi }{2} \)

LG d

\(f\left( x \right) = x - \sin 2x\) trên đoan \(\left[ { - {\pi  \over 2};\pi } \right]\).

Lời giải chi tiết:

\(f'\left( x \right) = 1 - 2\cos 2x;\)

\(f'\left( x \right) = 0 \Leftrightarrow \cos 2x = {1 \over 2} = \cos {\pi  \over 3}\) \( \Leftrightarrow 2x =  \pm {\pi  \over 3} + k2\pi \) \( \Leftrightarrow x =  \pm {\pi  \over 6} + k\pi ,k \in {\mathbb{Z}}\)

Với \( - {\pi  \over 2} < x < \pi ,f'\left( x \right) = 0\) tại các điểm \( - {\pi  \over 6},{\pi  \over 6}\) và \({{5\pi } \over 6}\)

Ta có \(f\left( { - {\pi  \over 6}} \right) =  - {\pi  \over 6} + {{\sqrt 3 } \over 2};\) \(f\left( {{\pi  \over 6}} \right) = {\pi  \over 6} - {{\sqrt 3 } \over 2};\) \(f\left( {{{5\pi } \over 6}} \right) = {{5\pi } \over 6} + {{\sqrt 3 } \over 2}\); \(f\left( { - {\pi  \over 2}} \right) =  - {\pi  \over 2};f\left( \pi  \right) = \pi \)
So sánh năm giá trị trên ta được:
\(\mathop {\max f\left( x \right)}\limits_{x \in \left[ { - {\pi  \over 2};\pi } \right]}  = {{5\pi } \over 6} + {{\sqrt 3 } \over 2}\) và \(\mathop {\min f\left( x \right)}\limits_{x \in \left[ { - {\pi  \over 2};\pi } \right]}  =  - {\pi  \over 2}\)

Loigiaihay.com


Bình chọn:
3.9 trên 8 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store