Đề kiểm tra giữa học kì 1 - Đề số 05
Đề bài
Cường độ điện trường là:
-
A.
Đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của từ trường tại một điểm
-
B.
Định luật vật lí đặc trưng cho tác dụng mạnh hay yếu của trường hấp dẫn tại một điểm
-
C.
Đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của trường trọng lực tại một điểm
-
D.
Đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của điện trường tại một điểm
Trong thời gian 30 giây có một điện lượng 60C chuyển qua tiết diện của dây. Số electron chuyển qua tiết điện trong thời gian 2 giây là:
-
A.
4.1019 electron
-
B.
2,5.1019 electron
-
C.
1,6.1019 electron
-
D.
1,25.1019 electron
Đặt một một điện tích dương vào trong điện trường có vectơ cường độ điện trường $\overrightarrow E $ .Hướng của lực điện tác dụng lên điện tích?
-
A.
Luôn cùng hướng với $\overrightarrow E $
-
B.
Vuông gốc với $\overrightarrow E $
-
C.
Luôn ngược hướng với $\overrightarrow E $
-
D.
Không có trường hợp nào
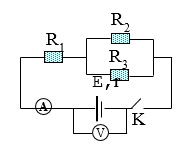
Cho mạch điện có sơ đồ như hình vẽ:
Biết R2 = 2\(\Omega \),R3 = 3\(\Omega \). Khi K mở, vôn kế chỉ 6V. Khi K đóng vôn kế chỉ 5,6V và ampe kế chỉ 2A.
Điện trở R1 có giá trị là:
-
A.
1,6$\Omega $
-
B.
2,8$\Omega $
-
C.
0,5$\Omega $
-
D.
1,2$\Omega $
Một hệ cô lập gồm 2 vật trung hoà về điện ta có thể làm cho chúng nhiễm điện trái dấu và có độ lớn bằng nhau bằng cách:
-
A.
Cho chúng tiếp xúc với nhau
-
B.
Cọ xát chúng với nhau
-
C.
Đặt 2 vật lại gần nhau
-
D.
Cả A, B, C đều đúng
Cách biểu diễn lực tương tác giữa hai điện tích đứng yên nào sau đây là sai?
-
A.
-
B.
-
C.
-
D.
Chọn một đáp án sai:
-
A.
cường độ dòng điện đo bằng ampe kế
-
B.
để đo cường độ dòng điện phải mắc nối tiếp ampe kế với mạch
-
C.
dòng điện qua ampe kế đi vào chốt dương, đi ra chốt âm của ampe kế
-
D.
dòng điện qua ampe kế đi vào chốt âm, đi ra chốt dương của ampe kế
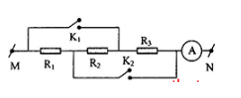
Cho mạch điện như hình vẽ: R2 = 10$\Omega $, UMN = 30V. Biết khi K1 đóng, K2 mở ampe kế chỉ 1A. Khi K1 mở, K2 đóng thì ampe kế A chỉ 2A. Số chỉ của ampe kế A khi cả 2 khóa K1 và K2 cùng đóng là?
-
A.
3A
-
B.
6A
-
C.
4A
-
D.
2A
Một điện tích q = 4.10-8C di chuyển trong một điện trường đều có cường độ E = 100V/m theo một đường gấp khúc ABC, đoạn AB = 20cm và véctơ độ dời \(\overrightarrow {AB} \) làm với đường sức điện một góc 300. Đoạn BC dài 40cm và véctơ độ dời \(\overrightarrow {BC} \)làm với đường sức điện một góc 1200 . Công của lực điện bằng:
-
A.
-1,07.10-7 J
-
B.
1,07.10-7 J
-
C.
2,4.10-6 J
-
D.
-8.10-7 J
Hai điện tích ${q_1} = {\rm{ }}8.{\rm{ }}{10^{ - 8}}C$, ${\rm{ }}{q_2} = {\rm{ }} - 8.{\rm{ }}{10^{ - 8}}C$ đặt tại $A$ và $B$ trong không khí biết $AB{\rm{ }} = {\rm{ }}4{\rm{ }}cm$. Tìm vectơ cường độ điện trường tại $C$ trên đường trung trực của $AB$ và cách $AB$ một khoảng $2{\rm{ }}cm$?
-
A.
${18.10^5}V/m$
-
B.
${9.10^5}V/m$
-
C.
$12,{73.10^5}V/m$
-
D.
$0{\rm{ }}V/m$
Một thanh bônit khi cọ xát với tấm dạ (cả hai cô lập với các vật khác) thì thu được điện tích \( - {3.10^{ - 8}}C\). Tấm dạ sẽ có điện tích:
-
A.
\( - {3.10^{ - 8}}C\)
-
B.
\( - {1,5.10^{ - 8}}C\)
-
C.
\({3.10^{ - 8}}C\)
-
D.
0
Đưa một thanh kim loại trung hoà về điện đặt trên một giá cách điện lại gần một quả cầu tích điện âm. Sau khi đưa thanh kim loại ra thật xa quả cầu thì thanh kim loại
-
A.
Có hai nữa tích điện trái dấu.
-
B.
Tích điện dương.
-
C.
Tích điện âm.
-
D.
Trung hoà về điện.
Hai điện tích \({q_1} = - q;{q_2} = 4q\) đặt cách nhau một khoảng r. Nếu điện tích \({q_1}\) tác dụng lực điện lên điện tích \({q_2}\) có độ lớn là F thì lực tác dụng của điện tích \({q_2}\) lên \({q_1}\) có độ lớn là:
-
A.
F.
-
B.
4F.
-
C.
2F.
-
D.
0,5F.
Tại ba đỉnh của tam giác đều \(ABC\), cạnh \(a = 10cm\) có ba điện tích điểm bằng nhau và bằng \(10nC\). Hãy xác định cường độ điện trường tại trung điểm của cạnh AB.
-
A.
\(12000V/m\)
-
B.
\(36000V/m\)
-
C.
\(84000V/m\)
-
D.
\(96000V/m\)
Lực điện trường là
-
A.
lực thế
-
B.
lực hấp dẫn
-
C.
lực đàn hồi
-
D.
lực ma sát
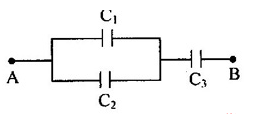
Cho ba tụ mắc như hình vẽ, với \({C_1} = 4\mu F\) có hiệu điện thế giới hạn là \(1000V\), \({C_2} = 2\mu F\) có hiệu điện thế giới hạn \(500V\), \({C_3} = 3\mu F\) có hiệu điện thế giới hạn là \(300V\). Hỏi hai đầu A, B mắc vào nguồn điện có hiệu điện thế tối đa bao nhiêu để bộ tụ không bị hỏng?
-
A.
\(450V\)
-
B.
\(2000V\)
-
C.
\(500V\)
-
D.
\(1000V\)
Thả một electron không vận tốc đầu ban đầu trong một điện trường bất kì, electron sẽ:
-
A.
chuyển động dọc theo một đường sức điện.
-
B.
chuyển động từ một điểm có điện thế cao xuống điểm có điện thế thấp.
-
C.
chuyển động từ một điểm có điện thế thấp lên điểm có điện thế cao.
-
D.
đứng yên.
Một electron có động năng \({{\rm{W}}_d} = 200eV\) lúc bắt đầu đi vào điện trường đều của hai bản kim loại đặt song song tích điện trái dấu theo hướng đường sức. Hỏi hiệu điện thế giữa hai bản phải là bao nhiêu để hạt không đến được bản đối diện. Biết \(1eV = 1,{6.10^{ - 19}}J\)
-
A.
\(U > 200V\)
-
B.
\(U = 200V\)
-
C.
\(U < 200V\)
-
D.
\(U \ne 200V\)
Một electron bay vào khoảng không giữa hai bản kim loại tích điện trái dấu với vận tốc \({v_0} = 2,{5.10^7}m/s\) từ phía bản dương về phía bản âm theo hướng hợp với bản dương góc \({15^0}\). Độ dài của mỗi bản là \(L = 5cm\) và khoảng cách giữa hai bản là \(d = 1cm\). Hãy tính hiệu điện thế giữa hai bản, biết rằng khi ra khỏi điện trường vận tốc của electron có phương song song với hai bản.
-
A.
\(535,5V\)
-
B.
\(711,7V\)
-
C.
\(177,7V\)
-
D.
\(355,5V\)
Một nguồn điện với suất điện động \(E\), điện trở trong \(r\), mắc với một điện trở ngoài \(R{\rm{ }} = {\rm{ }}r\) thì cường độ dòng điện chạy trong mạch là \(I\). Nếu thay nguồn điện đó bằng 3 nguồn điện giống hệt nó mắc nối tiếp thì cường độ dòng điện trong mạch
-
A.
vẫn bằng \(I\).
-
B.
bằng \(1,5I\).
-
C.
bằng \(\dfrac{I}{3}\).
-
D.
bằng \(0,5I\).
Cho mạch điện như hình vẽ:
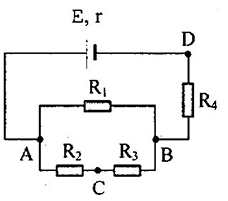
\(E = 9V,r = 1\Omega \), \({R_1} = {R_2} = {R_3} = 3\Omega \), \({R_4} = 6\Omega \). Tính cường độ dòng điện chạy qua \({R_1}\)
-
A.
\(\dfrac{1}{2}A\)
-
B.
\(1A\)
-
C.
\(\dfrac{1}{3}A\)
-
D.
\(\dfrac{2}{3}A\)
Một hạt bụi có khối lượng \(m = {10^{ - 11}}\,\,g\) nằm trong khoảng hai tấm kim loại song song nằm ngang và nhiễm điện trái dấu. Khoảng cách giữa hai bản \(d = 0,5\,\,cm\). Chiếu ánh sáng tử ngoại vào hạt bụi, do mất một phần điện tích, hạt bụi sẽ mất cân bằng. Để thiết lập lại cân bằng, người ta phải tăng hiệu điện thế giữa hai bản lên một lượng \(\Delta U = 34\,\,V\). Biết rằng hiệu điện thế giữa hai bản lúc đầu bằng \(306,3\,\,V\). Lấy \(g = 10\,\,m/{s^2}\). Điện lượng đã mất đi là?
-
A.
\(1,{63.10^{ - 19}}\,\,C\)
-
B.
\(1,{63.10^{ - 16}}\,\,C\)
-
C.
\(3,{26.10^{ - 16}}\,\,C\)
-
D.
\(3,{26.10^{ - 19}}\,\,C\)
Giả sử hiệu điện thế đặt vào hai đầu bóng đèn có ghi 220 V – 100W đột ngột tăng lên tới 240 V trong khoảng thời gian ngắn. Hỏi công suất điện của bóng đèn khi đó tăng lên hay giảm đi bao nhiêu phần trăm (%) so với công suất định mức của nó ? Cho rằng điện trở của bóng đèn không thay đổi so với khi hoạt động ở chế độ định mức
-
A.
tăng 29%
-
B.
giảm 29%
-
C.
giảm 19%
-
D.
tăng 19%
Cho hai quả cầu nhỏ trung hòa điện đặt trong không khí, cách nhau 40 cm. Giả sử có 4.1012 electron từ quả cầu này di chuyển sang quả cầu kia. Tính độ lớn của lực tương tác giữa hai quả cầu đó. Cho biết điện tích của electron bằng - 1,6.10−19 C
-
A.
2,304.10-3N
-
B.
2,304.10-4N
-
C.
2,304.10-2N
-
D.
2,304.10-5N
Hai quả cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5g, được treo vào cùng một điểm O bằng hai sợi dây không dãn, dài 10 cm. Tích điện cho mỗi quả cầu điện tích q như nhau thì thấy chúng đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 600. Tính độ lớn điện tích mà ta đã truyền cho hai quả cầu. Lấy g = 10 (m/s2).
-
A.
\(3,{6.10^{ - 7}}\;C\)
-
B.
\(1,{8.10^{ - 7}}\;C\)
-
C.
\(1,{6.10^{ - 7}}\;C\)
-
D.
\(3,{2.10^{ - 7}}\;C\)
Lời giải và đáp án
Cường độ điện trường là:
-
A.
Đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của từ trường tại một điểm
-
B.
Định luật vật lí đặc trưng cho tác dụng mạnh hay yếu của trường hấp dẫn tại một điểm
-
C.
Đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của trường trọng lực tại một điểm
-
D.
Đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của điện trường tại một điểm
Đáp án : D
Cường độ điện trường là đại lượng vật lí đặc trưng cho tác dụng mạnh hay yếu của điện trường tại một điểm
Trong thời gian 30 giây có một điện lượng 60C chuyển qua tiết diện của dây. Số electron chuyển qua tiết điện trong thời gian 2 giây là:
-
A.
4.1019 electron
-
B.
2,5.1019 electron
-
C.
1,6.1019 electron
-
D.
1,25.1019 electron
Đáp án : B
+ Áp dụng biểu thức xác định cường độ dòng điện:\(I = \frac{{\Delta q}}{{\Delta t}}\)
+ Áp dụng biểu thức xác định số electron chuyển qua dây dẫn trong thời gian t: \(n = \frac{{I.t}}{{\left| e \right|}}.\)
- Cường độ dòng điện:
\(I = \dfrac{{\Delta q}}{{\Delta t}} = 2A.\)
- Điện lượng chuyển qua tiết diện trong thời gian 2 giây:
\(\Delta q\, = \)I.t = 2.2 = 4C
- Số elcetron chuyển qua dây dẫn là:
\(n = \dfrac{{I.t}}{{|e|}} = 2,{5.10^{19}}electron.\)
Đặt một một điện tích dương vào trong điện trường có vectơ cường độ điện trường $\overrightarrow E $ .Hướng của lực điện tác dụng lên điện tích?
-
A.
Luôn cùng hướng với $\overrightarrow E $
-
B.
Vuông gốc với $\overrightarrow E $
-
C.
Luôn ngược hướng với $\overrightarrow E $
-
D.
Không có trường hợp nào
Đáp án : A
Ta có: \(\overrightarrow F = q.\overrightarrow E \), Nếu:
+ \(q{\text{ }} > {\text{ }}0 \to \overrightarrow F \uparrow \uparrow \overrightarrow E \)
+ \(q{\text{ }} < {\text{ }}0 \to \overrightarrow F \uparrow \downarrow \overrightarrow E \)
Cho mạch điện có sơ đồ như hình vẽ:
Biết R2 = 2\(\Omega \),R3 = 3\(\Omega \). Khi K mở, vôn kế chỉ 6V. Khi K đóng vôn kế chỉ 5,6V và ampe kế chỉ 2A.
Điện trở R1 có giá trị là:

-
A.
1,6$\Omega $
-
B.
2,8$\Omega $
-
C.
0,5$\Omega $
-
D.
1,2$\Omega $
Đáp án : A
+ Áp dụng biểu thức xác định điện trở tương đương của mạch
+ Áp dụng biểu thức độ giảm thế trên đoạn mạch: UN = I.RN = E - I.r
Ta có:
+ Khi k mở, vôn kế chỉ giá trị của suất điện động của nguồn:
Vì : UV = E - I.r có I = 0, vậy E = 6V.
+ Khi k đóng, vôn kế chỉ hiệu điện thế hai đầu nguồn điện:
Theo định luật Ôm, ta có:
\(I{\rm{ }} = \frac{{{U_V}}}{{{R_{td}}}} \to {R_{td}} = \frac{{{U_V}}}{I} = 2,8\Omega \).
Mạch ngoài gồm: R1 nt (R2 // R3)
\({R_{23}} = \frac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} = \frac{{2.3}}{{2 + 3}} = 1,2\Omega \)
R1 = Rtđ – R12 = 2,8 - 1,2 = 1,6\(\Omega \).
Một hệ cô lập gồm 2 vật trung hoà về điện ta có thể làm cho chúng nhiễm điện trái dấu và có độ lớn bằng nhau bằng cách:
-
A.
Cho chúng tiếp xúc với nhau
-
B.
Cọ xát chúng với nhau
-
C.
Đặt 2 vật lại gần nhau
-
D.
Cả A, B, C đều đúng
Đáp án : B
Ta có, khi 2 vật trung hòa về điện cọ xát nhau => một vật mất electron và một vật nhận electron. Số electron vật mất đi bằng số electron vật kia nhận
+ Vật mất e => mang điện dương
+ Vật nhận e => mang điện âm
Cách biểu diễn lực tương tác giữa hai điện tích đứng yên nào sau đây là sai?
-
A.
-
B.
-
C.
-
D.
Đáp án : B
Vận dụng lí thuyết tương tác điện tích
- Hai điện tích cùng dấu đẩy nhau
- Hai điện tích khác nhau (khác loại) hút nhau
Ta có:
- Hai điện tích cùng dấu đẩy nhau
- Hai điện tích khác nhau (khác loại) hút nhau
=> B - sai vì 2 điện tích cùng dấu mà lại hút nhau
Chọn một đáp án sai:
-
A.
cường độ dòng điện đo bằng ampe kế
-
B.
để đo cường độ dòng điện phải mắc nối tiếp ampe kế với mạch
-
C.
dòng điện qua ampe kế đi vào chốt dương, đi ra chốt âm của ampe kế
-
D.
dòng điện qua ampe kế đi vào chốt âm, đi ra chốt dương của ampe kế
Đáp án : D
Vận dụng lí thuyết về dụng cụ đo
A, B, C - đúng
D - sai vì: Dòng điện qua ampe kế đi vào từ cực dương và đi ra từ cực âm
Cho mạch điện như hình vẽ: R2 = 10$\Omega $, UMN = 30V. Biết khi K1 đóng, K2 mở ampe kế chỉ 1A. Khi K1 mở, K2 đóng thì ampe kế A chỉ 2A. Số chỉ của ampe kế A khi cả 2 khóa K1 và K2 cùng đóng là?

-
A.
3A
-
B.
6A
-
C.
4A
-
D.
2A
Đáp án : B
+ Áp dụng biểu thức xác định điện trở trong mạch song song:
\(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\)
+ Áp dụng biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \frac{U}{R}\)
Khi K1 đóng còn K2 mở thì mạch chỉ có R3 \( \to {R_3} = \frac{{30}}{1} = 30\Omega \)
Khi K2 đóng, K1 mở thì mạch chỉ có R1 \( \to {R_1} = \frac{{30}}{2} = 15\Omega \)
Khi K1 và K2 cùng đóng thì : R1 // R2 // R3:
Điện trở tương đương của mạch:
\(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} = \frac{1}{{15}} + \frac{1}{{10}} + \frac{1}{{30}} = \frac{1}{5} \to R = 5\Omega \)
Ta có, số chỉ ampe kế chính là I mạch chính: \(I = \frac{{{U_{MN}}}}{R} = \frac{{30}}{5} = 6A\)
Một điện tích q = 4.10-8C di chuyển trong một điện trường đều có cường độ E = 100V/m theo một đường gấp khúc ABC, đoạn AB = 20cm và véctơ độ dời \(\overrightarrow {AB} \) làm với đường sức điện một góc 300. Đoạn BC dài 40cm và véctơ độ dời \(\overrightarrow {BC} \)làm với đường sức điện một góc 1200 . Công của lực điện bằng:
-
A.
-1,07.10-7 J
-
B.
1,07.10-7 J
-
C.
2,4.10-6 J
-
D.
-8.10-7 J
Đáp án : A
Áp dụng công thức tính công của lực điện: A = qEd
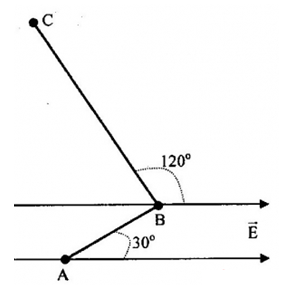
Từ hình, ta có:
\(\left\{ \begin{array}{l}{d_{AB}} = ABc{\rm{os3}}{{\rm{0}}^0} = 20.\frac{{\sqrt 3 }}{2} = 10\sqrt 3 cm\\{d_{BC}} = BCc{\rm{os12}}{{\rm{0}}^0} = 40.\left( { - \frac{1}{2}} \right) = - 20cm\end{array} \right.\)
Công của lực điện khi làm điện tích q di chuyển theo đường gấp khúc ABC là:
\(\begin{array}{l}A = {A_{AB}} + {A_{BC}} = qE\left( {{d_{AB}} + {d_{BC}}} \right)\\ = {4.10^{ - 8}}.100(0,1\sqrt 3 + ( - 0,2))\\ = - 1,{07.10^{ - 7}}J\end{array}\)
Hai điện tích ${q_1} = {\rm{ }}8.{\rm{ }}{10^{ - 8}}C$, ${\rm{ }}{q_2} = {\rm{ }} - 8.{\rm{ }}{10^{ - 8}}C$ đặt tại $A$ và $B$ trong không khí biết $AB{\rm{ }} = {\rm{ }}4{\rm{ }}cm$. Tìm vectơ cường độ điện trường tại $C$ trên đường trung trực của $AB$ và cách $AB$ một khoảng $2{\rm{ }}cm$?
-
A.
${18.10^5}V/m$
-
B.
${9.10^5}V/m$
-
C.
$12,{73.10^5}V/m$
-
D.
$0{\rm{ }}V/m$
Đáp án : C
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
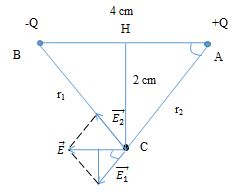
- Ta có: \({r_1} = {\rm{ }}{r_2} = r = \sqrt {A{H^2} + A{C^2}} = 2\sqrt 2 \) cm Vì \(\left| {{q_1}} \right|{\rm{ }} = {\rm{ }}\left| {{q_2}} \right|\) và \({r_1} = {\rm{ }}{r_2}\) \( = > {E_1} = {\rm{ }}{E_2}\)
- Từ hình vẽ ta có: $E = 2{E_1}c{\rm{os}}\alpha $
Với \(\cos \alpha = \dfrac{{AH}}{{AC}} = \dfrac{2}{{2\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}\)
=> \(E = 2{E_1}\dfrac{{\sqrt 2 }}{2} = {E_1}\sqrt 2 \)
Ta có: \({E_1} = k\dfrac{{\left| {{q_2}} \right|}}{{\varepsilon .{r_1}^2}} = {9.10^9}\dfrac{{\left| {{{8.10}^{ - 8}}} \right|}}{{1.{{(2.\sqrt 2 {{.10}^{ - 2}})}^2}}} = {9.10^5}V/m\)
\( \to E = \sqrt 2 {.9.10^5} \approx {\rm{ }}12,73.{\rm{ }}{10^5}V/m\)
Một thanh bônit khi cọ xát với tấm dạ (cả hai cô lập với các vật khác) thì thu được điện tích \( - {3.10^{ - 8}}C\). Tấm dạ sẽ có điện tích:
-
A.
\( - {3.10^{ - 8}}C\)
-
B.
\( - {1,5.10^{ - 8}}C\)
-
C.
\({3.10^{ - 8}}C\)
-
D.
0
Đáp án : C
Vận dụng lí thuyết về nhiễm điện do cọ xát và thuyết electron giải thích sự nhiễm điện do cọ xát
Độ lớn điện tích trên tấm dạ chính bằng độ lớn điện tích mà thanh bônít thu được và điện tích trên tấm dạ sẽ trái dấu với điện tích của thanh bônít
=> Tấm dạ sẽ có điện tích là: \({3.10^8}C\)
Đưa một thanh kim loại trung hoà về điện đặt trên một giá cách điện lại gần một quả cầu tích điện âm. Sau khi đưa thanh kim loại ra thật xa quả cầu thì thanh kim loại
-
A.
Có hai nữa tích điện trái dấu.
-
B.
Tích điện dương.
-
C.
Tích điện âm.
-
D.
Trung hoà về điện.
Đáp án : D
Ta có, khi đưa thanh kim loại ra thật xa quả cầu thì thanh kim loại trở về trạng thái không nhiễm điện như lúc đầu tức là trung hòa về điện
Hai điện tích \({q_1} = - q;{q_2} = 4q\) đặt cách nhau một khoảng r. Nếu điện tích \({q_1}\) tác dụng lực điện lên điện tích \({q_2}\) có độ lớn là F thì lực tác dụng của điện tích \({q_2}\) lên \({q_1}\) có độ lớn là:
-
A.
F.
-
B.
4F.
-
C.
2F.
-
D.
0,5F.
Đáp án : A
Áp dụng định luật Cu-lông: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Theo định luật Cu-lông ta có: Lực tác dụng của điện tích \({q_1}\) lên \({q_2}\) và lực tác dụng của điện tích \({q_2}\) lên \({q_1}\) bằng nhau: \({F_{12}} = {F_{21}} = F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
Tại ba đỉnh của tam giác đều \(ABC\), cạnh \(a = 10cm\) có ba điện tích điểm bằng nhau và bằng \(10nC\). Hãy xác định cường độ điện trường tại trung điểm của cạnh AB.
-
A.
\(12000V/m\)
-
B.
\(36000V/m\)
-
C.
\(84000V/m\)
-
D.
\(96000V/m\)
Đáp án : A
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Gọi \(H\) - trung điểm của cạnh \(AB\)
Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) lần lượt là cường độ điện trường do điện tích \({q_1},{q_2},{q_3}\) gây ra tại \(H\)
Ta có, các véc-tơ \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) được biểu diễn như hình
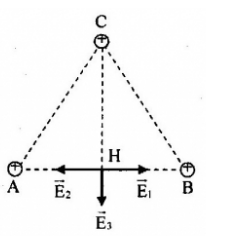
Ta có: \({E_1} = {E_2} = k\dfrac{{\left| q \right|}}{{{{\left( {\dfrac{{AB}}{2}} \right)}^2}}}\)
\({E_3} = k\dfrac{{\left| q \right|}}{{C{H^2}}}\)
Lại có:
\(\begin{array}{l}CH = \sqrt {C{B^2} - B{H^2}} = \sqrt {C{B^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}} \\ = \sqrt {{{10}^2} - \dfrac{{{{10}^2}}}{4}} = 5\sqrt 3 cm\end{array}\)
Ta suy ra: \({E_3} = {9.10^9}\dfrac{{{{10.10}^{ - 9}}}}{{{{\left( {5\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 12000V/m\)
Ta có, cường độ điện trường tổng hợp tại \(H\): \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
Vì \(\left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_1} = {E_2}\end{array} \right. \Rightarrow \overrightarrow {{E_{12}}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow 0 \)
Ta suy ra: \(\overrightarrow E = \overrightarrow {{E_3}} \)
\( \Rightarrow E = {E_3} = 12000V/m\)
Lực điện trường là
-
A.
lực thế
-
B.
lực hấp dẫn
-
C.
lực đàn hồi
-
D.
lực ma sát
Đáp án : A
Lực điện trường là lực thế vì công của lực điện trường không phụ thuộc vào hình dạng đường đi mà chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối của điện tích
Cho ba tụ mắc như hình vẽ, với \({C_1} = 4\mu F\) có hiệu điện thế giới hạn là \(1000V\), \({C_2} = 2\mu F\) có hiệu điện thế giới hạn \(500V\), \({C_3} = 3\mu F\) có hiệu điện thế giới hạn là \(300V\). Hỏi hai đầu A, B mắc vào nguồn điện có hiệu điện thế tối đa bao nhiêu để bộ tụ không bị hỏng?

-
A.
\(450V\)
-
B.
\(2000V\)
-
C.
\(500V\)
-
D.
\(1000V\)
Đáp án : A
+ Vận dụng biểu thức tính điện dung của tụ khi ghép nối tiếp: \(\dfrac{1}{{{C_{nt}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ... + \dfrac{1}{{{C_n}}}\)
+ Vận dụng biểu thức tính điện dung của tụ khi ghép song song: \({C_{//}} = {\rm{ }}{C_1} + {\rm{ }}{C_2} + {\rm{ }} \ldots + {\rm{ }}{C_n}\)
+ Vận dụng biểu thức tính điện tích: \(Q = CU\)
+ Điều kiện để tụ không bị đánh thủng
Gọi \(U\) là hiệu điện thế của bộ tụ
+ Từ mạch, ta có: \(\left( {{C_1}//{C_2}} \right)nt{C_3}\)
\({C_{12}} = {C_1} + {C_2} = 4 + 2 = 6\mu F\)
Điện dung của toàn mạch: \(\dfrac{1}{C} = \dfrac{1}{{{C_{12}}}} + \dfrac{1}{{{C_3}}}\)
\( \Rightarrow C = \dfrac{{{C_{12}}{C_3}}}{{{C_{12}} + {C_3}}} = \dfrac{{6.3}}{{6 + 3}} = 2\mu F\)
\( \Rightarrow Q = CU = 2U = {Q_{12}} = {Q_3}\)
+ Điều kiện để bộ tụ tồn tại: \(\left\{ \begin{array}{l}{U_1} = \dfrac{{{Q_{12}}}}{{{C_1}}} = \dfrac{{2U}}{4} \le 1000V\\{U_2} = \dfrac{{{Q_{12}}}}{{{C_2}}} = \dfrac{{2U}}{2} = U \le 500V\\{U_3} = \dfrac{{{Q_3}}}{{{C_3}}} = \dfrac{{2U}}{3} \le 300V\end{array} \right. \Rightarrow \left\{ \begin{array}{l}U \le 2000V\\U \le 500V\\U \le 450V\end{array} \right. \Rightarrow U \le 450V\)
Vậy, cần mắc hai đầu A, B vào nguồn điện có hiệu điện thế tối đa \(450V\) để bộ tụ không bị hỏng.
Thả một electron không vận tốc đầu ban đầu trong một điện trường bất kì, electron sẽ:
-
A.
chuyển động dọc theo một đường sức điện.
-
B.
chuyển động từ một điểm có điện thế cao xuống điểm có điện thế thấp.
-
C.
chuyển động từ một điểm có điện thế thấp lên điểm có điện thế cao.
-
D.
đứng yên.
Đáp án : C
Vận dụng lí thuyết về chuyển động của điện tích trong điện trường
Cường độ điện trường hướng từ nơi có điện thế cao đến nơi có điện thế thấp.
Electron mang điện tích âm nên chịu tác dụng của lực điện trường và lực điện ngược chiều với cường độ điện trường.
=> Electron sẽ chuyển động từ một điểm có điện thế thấp lên điểm có điện thế cao.
Một electron có động năng \({{\rm{W}}_d} = 200eV\) lúc bắt đầu đi vào điện trường đều của hai bản kim loại đặt song song tích điện trái dấu theo hướng đường sức. Hỏi hiệu điện thế giữa hai bản phải là bao nhiêu để hạt không đến được bản đối diện. Biết \(1eV = 1,{6.10^{ - 19}}J\)
-
A.
\(U > 200V\)
-
B.
\(U = 200V\)
-
C.
\(U < 200V\)
-
D.
\(U \ne 200V\)
Đáp án : A
+ Sử dụng định lí biến thiên động năng: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = {A_{ngoailuc}}\)
+ Sử dụng biểu thức liên hệ giữa cường độ điện trường và hiệu điện thế: \(E = \dfrac{U}{d}\)
Khi electron chuyển động từ bản này đến bản kia, thì nó chịu tác dụng của ngoại lực là lực điện trường.
+ Theo định lí động năng, ta có: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = qE{d_{12}}\)
\( \Rightarrow {d_{12}} = \dfrac{{ - {{\rm{W}}_{{d_1}}}}}{{qE}} = \dfrac{{ - 200.1,{{6.10}^{ - 19}}}}{{ - 1,{{6.10}^{ - 19}}.E}} = \dfrac{{200}}{E}\)
+ Để electron không đến được bản đối diện thì quãng đường nó đi được phải nhỏ hơn khoảng cách giữa hai bản này hay \({d_{12}} < d\) (1)
Lại có: \(d = \dfrac{U}{E}\) (2)
Từ (1) và (2) ta suy ra: \(\dfrac{{200}}{E} < \dfrac{U}{E} \Rightarrow U > 200V\)
Một electron bay vào khoảng không giữa hai bản kim loại tích điện trái dấu với vận tốc \({v_0} = 2,{5.10^7}m/s\) từ phía bản dương về phía bản âm theo hướng hợp với bản dương góc \({15^0}\). Độ dài của mỗi bản là \(L = 5cm\) và khoảng cách giữa hai bản là \(d = 1cm\). Hãy tính hiệu điện thế giữa hai bản, biết rằng khi ra khỏi điện trường vận tốc của electron có phương song song với hai bản.
-
A.
\(535,5V\)
-
B.
\(711,7V\)
-
C.
\(177,7V\)
-
D.
\(355,5V\)
Đáp án : C
+ Vận dụng các biểu thức của dạng bài toán ném xiên
+ Sử dụng biểu thức tính lực điện: \(\overrightarrow F = q\overrightarrow E \)
+ Sử dụng biểu thức liên hệ giữa hiệu điện thế và cường độ điện trường: \(E = \dfrac{U}{d}\)
+ Sử dụng công thức lượng giác: \(\sin 2\alpha = 2\sin \alpha c{\rm{os}}\alpha \)
+ Chọn hệ trục \(xOy\) như hình

+ Ta có, chuyển động của hạt được phân tích thành hai chuyển động.
- Theo phương ngang (Ox): hạt chuyển động thẳng đều với vận tốc ban đầu \({v_{0x}} = {v_0}cos\alpha \)
- Theo phương Oy: hạt chuyển động biến đổi đều với vận tốc đầu: \({v_{0y}} = {v_0}\sin \alpha \)
+ Phương trình vận tốc theo các trục: \(\left\{ \begin{array}{l}{v_x} = {v_0}cos\alpha \\{v_y} = {v_0}\sin \alpha + at\end{array} \right.\)
+ Vì khi ra khỏi điện trường, vận tốc có phương ngang nên thành phần \({v_y} = 0\) do đó ta có:
\({v_0}\sin \alpha + at = 0 \Rightarrow t = \dfrac{{ - {v_0}\sin \alpha }}{a}\) (1)
+ Phương trình chuyển động theo phương Ox: \(x = \left( {{v_0}cos\alpha } \right)t\)
Khi ra khỏi điện trường thì \(x = L \Leftrightarrow \left( {{v_0}cos\alpha } \right)t = L\) (2)
Từ (1) và (2), ta có: \(\left( {{v_0}cos\alpha } \right)\dfrac{{ - {v_0}\sin \alpha }}{a} = L\) (3)
+ Mặt khác, ta có gia tốc của electron khi chuyển động trong điện trường: \(a = \dfrac{{ - F}}{m} = \dfrac{{ - \left| q \right|E}}{m} = \dfrac{{ - \left| q \right|U}}{{md}}\) (4)
Từ (3) và (4), ta có:
\(\eqalign{
& \left( {{v_0}cos\alpha } \right){{ - {v_0}\sin \alpha } \over {{{ - \left| q \right|U} \over {md}}}} = L \cr
& \Rightarrow U = {{mdv_0^2.\sin 2\alpha } \over {2\left| q \right|L}} = {{\left( {9,{{1.10}^{ - 31}}} \right).\left( {0,01} \right).{{\left( {2,{{5.10}^7}} \right)}^2}.\sin {{30}^0}} \over 2.{1,{{6.10}^{ - 19}}.0,05}} = 177,7V \cr} \)
Một nguồn điện với suất điện động \(E\), điện trở trong \(r\), mắc với một điện trở ngoài \(R{\rm{ }} = {\rm{ }}r\) thì cường độ dòng điện chạy trong mạch là \(I\). Nếu thay nguồn điện đó bằng 3 nguồn điện giống hệt nó mắc nối tiếp thì cường độ dòng điện trong mạch
-
A.
vẫn bằng \(I\).
-
B.
bằng \(1,5I\).
-
C.
bằng \(\dfrac{I}{3}\).
-
D.
bằng \(0,5I\).
Đáp án : B
+ Áp dụng biểu thức định luật Ôm cho toàn mạch
+ Áp dụng biểu thức xác định \({E_b}\) khi mắc nguồn nối tiếp: \({E_b} = {E_1} + {E_2} + ...\)
+ Áp dụng biểu thức xác định rb khi mắc nguồn nối tiếp: \({r_b} = {r_1} + {r_2} + ...\)
- Khi mắc với một điện trở ngoài \(R{\rm{ }} = {\rm{ }}r\)
Cường độ dòng điện \(I = \dfrac{E}{{R + r}} = \dfrac{E}{{r + r}} = \dfrac{E}{{2{\rm{r}}}}\)
- Khi thay nguồn bằng 3 nguồn điện giống hệt mắc nối tiếp:
\(\left\{ \begin{array}{l}{E_b} = {E_1} + {E_2} + {E_3} = 3E\\{r_b} = {r_1} + {r_2} + {r_3} = 3r\end{array} \right.\)
Cường độ dòng điện khi này: \(I' = \dfrac{{{E_b}}}{{R + {r_n}}} = \dfrac{{3E}}{{r + 3r}} = \dfrac{{3E}}{{{\rm{4r}}}}\)
\(\dfrac{{I'}}{I} = \dfrac{{\dfrac{{3E}}{{4r}}}}{{\dfrac{E}{{2r}}}} = \dfrac{3}{2} \to I' = 1,5I\)
Cho mạch điện như hình vẽ:

\(E = 9V,r = 1\Omega \), \({R_1} = {R_2} = {R_3} = 3\Omega \), \({R_4} = 6\Omega \). Tính cường độ dòng điện chạy qua \({R_1}\)
-
A.
\(\dfrac{1}{2}A\)
-
B.
\(1A\)
-
C.
\(\dfrac{1}{3}A\)
-
D.
\(\dfrac{2}{3}A\)
Đáp án : D
+ Sử dụng biểu thức tính điện trở tương đương của các điện trở mắc nối tiếp: \(R = {R_1} + {R_2} + ...\)
+ Sử dụng biểu thức tính điện trở tương đương của các điện trở mắc song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ...\)
+ Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{E}{{{R_N} + r}}\)
+ Sử dụng biểu thức định luật ôm.
+ Từ mạch điện ta thấy: \(\left( {\left[ {{R_2}nt{R_3}} \right]//{R_1}} \right)nt{R_4}\)
\({R_{23}} = {R_2} + {R_3} = 3 + 3 = 6\Omega \)
\({R_{AB}} = \dfrac{{{R_1}{R_{23}}}}{{{R_1} + {R_{23}}}} = \dfrac{{3.6}}{{3 + 6}} = 2\Omega \)
Tổng trở của mạch ngoài: \({R_N} = {R_{AB}} + {R_4} = 2 + 6 = 8\Omega \)
+ Cường độ dòng điện trong mạch chính: \(I = \dfrac{E}{{{R_N} + r}} = \dfrac{9}{{8 + 1}} = 1A\)
\({I_4} = {I_{AB}} = I = 1A\)
+ Hiệu điện thế giữa hai điểm A, B: \({U_{AB}} = {I_{AB}}.{R_{AB}} = 1.2 = 2V\)
Suy ra: \({U_1} = {U_{23}} = 2V\)
+ Dòng điện chạy qua \({R_1}\): \({I_1} = \dfrac{{{U_1}}}{{{R_1}}} = \dfrac{2}{3}\left( A \right)\)
Vậy, cường độ dòng điện qua \({R_1}\) là \(\dfrac{2}{3}A\)
Một hạt bụi có khối lượng \(m = {10^{ - 11}}\,\,g\) nằm trong khoảng hai tấm kim loại song song nằm ngang và nhiễm điện trái dấu. Khoảng cách giữa hai bản \(d = 0,5\,\,cm\). Chiếu ánh sáng tử ngoại vào hạt bụi, do mất một phần điện tích, hạt bụi sẽ mất cân bằng. Để thiết lập lại cân bằng, người ta phải tăng hiệu điện thế giữa hai bản lên một lượng \(\Delta U = 34\,\,V\). Biết rằng hiệu điện thế giữa hai bản lúc đầu bằng \(306,3\,\,V\). Lấy \(g = 10\,\,m/{s^2}\). Điện lượng đã mất đi là?
-
A.
\(1,{63.10^{ - 19}}\,\,C\)
-
B.
\(1,{63.10^{ - 16}}\,\,C\)
-
C.
\(3,{26.10^{ - 16}}\,\,C\)
-
D.
\(3,{26.10^{ - 19}}\,\,C\)
Đáp án : A
Hạt bụi cân bằng khi các lực tác dụng lên nó cân bằng
Mối liên hệ giữa cường độ điện trường và hiệu điện thế U = E.d
Các lực tác dụng lên hạt bụi gồm: Trọng lực \(\overrightarrow P \) , lực điện \(\overrightarrow F \)
Điều kiện cân bằng của hạt bụi: \(\overrightarrow F + \overrightarrow P = 0 \to F = P \leftrightarrow qE = mg \to q = \frac{{mg}}{E}\)
Mặt khác: \(E = \frac{U}{d} \to q = \frac{{mg}}{{\frac{U}{d}}} = \frac{{mgd}}{U}\)
Áp dụng cho lúc đầu và lúc sau, ta có: \(\left\{ \begin{array}{l}{q_1} = \frac{{mg{\rm{d}}}}{U}\\{q_2} = \frac{{mg{\rm{d}}}}{{U + \Delta U}}\end{array} \right.\)
\( \to \Delta q = {q_1} - {q_2} = mg{\rm{d}}\left( {\frac{1}{U} - \frac{1}{{U + \Delta U}}} \right) = {10^{ - 11}}{\rm{.1}}{{\rm{0}}^{ - 3}}{\rm{.10}}{\rm{.0,005}}{\rm{.}}\left( {\frac{1}{{306,3}} - \frac{1}{{306,3 + 34}}} \right) = 1,{63.10^{ - 19}}C\)
Giả sử hiệu điện thế đặt vào hai đầu bóng đèn có ghi 220 V – 100W đột ngột tăng lên tới 240 V trong khoảng thời gian ngắn. Hỏi công suất điện của bóng đèn khi đó tăng lên hay giảm đi bao nhiêu phần trăm (%) so với công suất định mức của nó ? Cho rằng điện trở của bóng đèn không thay đổi so với khi hoạt động ở chế độ định mức
-
A.
tăng 29%
-
B.
giảm 29%
-
C.
giảm 19%
-
D.
tăng 19%
Đáp án : D
Phương pháp:
Công suất: \(P = UI = \frac{{{U^2}}}{R}\)
Cách giải:
Điện trở của bóng đèn là: \(R = \frac{{{U^2}}}{P} = \frac{{{{220}^2}}}{{100}} = 484\Omega \)
Khi hiệu điện thế tăng lên tới 240V. Công suất của đèn khi đó là:
\(P' = \frac{{U{'^2}}}{R} = \frac{{{{240}^2}}}{{484}} = 119W\)
→ Công suất này tăng 19% so với công suất định mức: P = 19%.Pđm
Cho hai quả cầu nhỏ trung hòa điện đặt trong không khí, cách nhau 40 cm. Giả sử có 4.1012 electron từ quả cầu này di chuyển sang quả cầu kia. Tính độ lớn của lực tương tác giữa hai quả cầu đó. Cho biết điện tích của electron bằng - 1,6.10−19 C
-
A.
2,304.10-3N
-
B.
2,304.10-4N
-
C.
2,304.10-2N
-
D.
2,304.10-5N
Đáp án : C
Công thức tính lực tương tác: \(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}\)
Quả cầu mất electron sẽ nhiễm điện dương, quả cầu nhận electron sẽ nhiễm điện âm
Độ lớn của điện tích trên mỗi quả cầu :
\(\left| {{q}_{1}} \right|=\left| {{q}_{2}} \right|={{4.10}^{12}}.\left| -1,{{6.10}^{-19}} \right|=6,{{4.10}^{-7}}C\)
Lực tương tác giữa hai quả cầu:
\(F=k\frac{\left| {{q}_{1}}{{q}_{2}} \right|}{{{r}^{2}}}={{9.10}^{9}}.\frac{{{\left( 6,{{4.10}^{-7}} \right)}^{2}}}{{{\left( {{40.10}^{-2}} \right)}^{2}}}=2,{{304.10}^{-2}}N\)
Hai quả cầu nhỏ giống nhau bằng kim loại có khối lượng m = 5g, được treo vào cùng một điểm O bằng hai sợi dây không dãn, dài 10 cm. Tích điện cho mỗi quả cầu điện tích q như nhau thì thấy chúng đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 600. Tính độ lớn điện tích mà ta đã truyền cho hai quả cầu. Lấy g = 10 (m/s2).
-
A.
\(3,{6.10^{ - 7}}\;C\)
-
B.
\(1,{8.10^{ - 7}}\;C\)
-
C.
\(1,{6.10^{ - 7}}\;C\)
-
D.
\(3,{2.10^{ - 7}}\;C\)
Đáp án : A
Định luật Cu – lông \(F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Điều kiện cân bằng: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + ... + \overrightarrow {{F_n}} = 0\)
Phân tích các lực tác dụng vào vật trên hình vẽ và sử dụng các kiến thức hình học.
Khi quả cầu cân bằng thì: \(\overrightarrow P + \overrightarrow T + \overrightarrow {{F_d}} = 0\)
Đặt \(\overrightarrow {T'} = \overrightarrow P + \overrightarrow {{F_d}} \Rightarrow \overrightarrow {T'} + \overrightarrow T = 0 \Rightarrow \left\{ \begin{array}{l}\overrightarrow {T'} \, \uparrow \downarrow \overrightarrow T \\T' = T\end{array} \right.\)
Biểu diễn các lực tác dụng lên quả cầu:
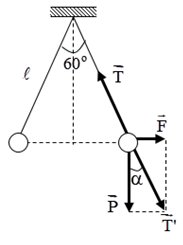
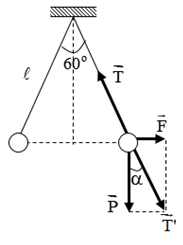
+ Từ hình vẽ ta có:
\(\begin{array}{l}\tan \alpha = \dfrac{{{F_d}}}{P} \Rightarrow {F_d} = P.\tan \alpha = mg.\tan \alpha \\ \Rightarrow {F_d} = {5.10^{ - 3}}.10.\tan 30 = 0,029N\end{array}\)
+ Khi hai dây treo hợp với nhau một góc 600thì khoảng cách giữa hai điện tích bằng:
\(l = 10cm = 0,1m\)
+ Mà: \(\left\{ \begin{array}{l}F = \dfrac{{k\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\\\left| {{q_1}} \right| = \left| {{q_1}} \right| = \left| q \right|\end{array} \right. \Rightarrow F = k.\dfrac{{{q^2}}}{{{l^2}}} \Rightarrow \left| q \right| = \sqrt {\dfrac{{F.{l^2}}}{k}} \)
Thay số ta được: \(\left| q \right| = \sqrt {\dfrac{{0,029.0,{1^2}}}{{{{9.10}^9}}}} = 1,{8.10^{ - 7}}C\)
+ Vậy tổng độ lớn điện tích đã truyền cho hai quả cầu là: \(Q = 2.\left| q \right| = 3,{6.10^{ - 7}}\;C\)
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |




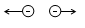
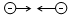
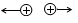
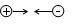






Danh sách bình luận