Đề kiểm tra 1 tiết chương 1: Điện tích - Điện trường - Đề số 03
Đề bài
Biểu thức nào sau đây xác định công của lực điện?
-
A.
A = qUd
-
B.
A = qEd
-
C.
A = qE
-
D.
\(A = \frac{{qE}}{d}\)
Hai điện tích điểm q1 = +3 (µC) và q2 = -3 (µC), đặt trong dầu (ε = 2) cách nhau một khoảng r = 3 (cm). Lực tương tác giữa hai điện tích đó là:
-
A.
lực hút với độ lớn F = 45 (N).
-
B.
lực đẩy với độ lớn F = 45 (N).
-
C.
lực hút với độ lớn F = 90 (N).
-
D.
lực đẩy với độ lớn F = 90 (N).
Nguyên tử trung hòa về điện, khi mất bớt electron sẽ trở thành:
-
A.
Ion-
-
B.
Ion+
-
C.
Không xác định được
-
D.
Không có gì thay đổi
Ta tích điện cho tụ bằng cách:
-
A.
Nối tụ với nguồn xoay chiều
-
B.
Nối tụ với nguồn pin một chiều
-
C.
Nối tụ với nguồn xoay chiều hoặc nguồn một chiều
-
D.
Không tích được điện cho tụ
Xét các trường hợp sau với quả cầu B đang trung hòa điện:
I- Quả cầu A mang điện dương đặt gần quả cầu B bằng sắt
II- Quả cầu A mang điện dương đặt gần quả cầu B bằng sứ
III- Quả cầu A mang điện âm đặt gần quả cầu B bằng thủy tinh
IV- Quả cầu A mang điện âm đặt gần quả cầu B bằng đồng
Những trường hợp nào trên đây có sự nhiễm điện của quả cầu B
-
A.
I và III
-
B.
III và IV
-
C.
II và IV
-
D.
I và IV
Có hai điện tích ${q_1} = {\rm{ }}q{\rm{ }} < {\rm{ }}0$ và ${q_2} = {\rm{ }}4q$ đặt cố định trong không khí cách nhau một khoảng $a{\rm{ }} = {\rm{ }}30cm$. Phải đặt một điện tích ${q_3}$ cách ${q_1}$ một khoảng $l$ bao nhiêu để nó cân bằng?
-
A.
$l = 10cm$
-
B.
$l = 20cm$
-
C.
$l = 15cm$
-
D.
$l = 35cm$
Điện tích điểm là:
-
A.
Một vật tích điện có kích thước nhỏ so với khoảng cách điểm mà ta đang xét
-
B.
Một vật tích điện có kích thước rất lớn so với khoảng cách điểm mà ta đang xét
-
C.
Một vật tích điện có kích thước lớn so với khoảng cách điểm mà ta đang xét
-
D.
Một vật tích điện có kích thước rất nhỏ so với khoảng cách điểm mà ta đang xét
Hai điện tích q1 = 8. 10-8 C, q2 = -8. 10-8 C đặt tại A và B trong không khí biết AB = 4 cm. Tìm vectơ cường độ điện trường tại C trên đường trung trực của AB và cách AB 2 cm?
-
A.
18.105 V/m
-
B.
9.105 V/m
-
C.
12,73.105 V/m
-
D.
0 V/m
Có 3 điện tích điểm q1 = 15.10-9C; q2 = -12.10-9C; q3 = 7.10-9C đặt tại ba đỉnh của tam giác đều ABC, cạnh 10cm. Điện thế tại tâm O và H - chân đường cao từ A xuống BC do ba điện tích gây ra là?
-
A.
V0 = 15,58V; VH = 658,8V
-
B.
V0 = 658,8V; VH = 658,8V
-
C.
V0 = 1558,8V; VH = 658,8V
-
D.
V0 = 658,8V; VH = 1658,8V
Một điện tích q chuyển động trong điện trường không đều theo một đường cong kín. Gọi công của lực điện trong chuyển động đó là A thì
-
A.
A ≥ 0 nếu q > 0.
-
B.
A > 0 nếu q < 0.
-
C.
A = 0 trong mọi trường hợp.
-
D.
A ≠ 0 còn dấu của A chưa xác định vì chưa biết chiều chuyển động của q.
Cho các yếu tố sau:
I- Độ lớn của các điện tích
II- Dấu của các điện tích
III- Bản chất của điện môi
IV- Khoảng cách giữa hai điện tích
Độ lớn của lực tương tác giữa hai điện tích điểm đứng yên trong môi trường điện môi đồng chất phụ thuộc vào những yếu tố nào sau đây?
-
A.
II và III
-
B.
I, II và III
-
C.
I, III và IV
-
D.
Cả bốn yếu tố
Một điện tích q = 4.10-8C di chuyển trong một điện trường đều có cường độ E = 100V/m theo một đường gấp khúc ABC, đoạn AB = 20cm và véctơ độ dời \(\overrightarrow {AB} \) làm với đường sức điện một góc 300. Đoạn BC dài 40cm và véctơ độ dời \(\overrightarrow {BC} \)làm với đường sức điện một góc 1200 . Công của lực điện bằng:
-
A.
-1,07.10-7 J
-
B.
1,07.10-7 J
-
C.
2,4.10-6 J
-
D.
-8.10-7 J
Bốn tụ điện như nhau, mỗi tụ có điện dung \(C\) được ghép song song với nhau. Điện dung của bộ tụ điện đó bằng:
-
A.
\(4C\)
-
B.
\(2C\)
-
C.
\(0,5C\)
-
D.
\(0,25C\)
Cho \({q_1} = {3.10^{ - 10}}C,{\rm{ }}{q_2} = - {3.10^{ - 10}}C\), đặt tại A và B trong dầu có \(\varepsilon = 2\) biết \(AB = 2{\rm{ }}cm\) . Xác định vectơ \(\vec E\) tại điểm \(H\) - là trung điểm của \(AB\).
-
A.
\({27.10^3}V/m\)
-
B.
\({13,5.10^3}V/m\)
-
C.
\(0{\rm{ }}V/m\)
-
D.
\({36.10^5}V/m\)
Một con lắc đơn gồm một quả cầu tích điện dương khối lượng \(\sqrt 3 g\) buộc vào sợi dây mảnh cách điện. Con lắc treo trong điện trường đều có phương nằm ngang với cường độ điện trường \(10000{\rm{ }}V/m\). Tại nơi có \(g = 9,8m/{s^2}\). Khi vật ở vị trí cân bằng, sợi dây lệch một góc \(\alpha = {\rm{ }}{30^0}\) so với phương thẳng đứng. Độ lớn của điện tích của quả cầu là:
-
A.
\({4.10^{ - 7}}C\)
-
B.
\({3,27.10^{ - 7}}C\)
-
C.
\({9,8.10^{ - 7}}C\)
-
D.
\({10^{ - 7}}C\)
Đồ thị nào trong các đồ thị dưới đây có thể biểu diễn sự phụ thuộc của lực tương tác giữa hai điện tích điểm vào khoảng cách giữa chúng?
-
A.
-
B.
-
C.
-
D.
Theo nội dung của thuyết electron, phát biểu nào sau đây là đúng?
-
A.
Electron không thể rời khỏi nguyên tử để di chuyển từ nơi này đến nơi khác
-
B.
Vật nhiễm điện âm khi chỉ số electron mà nó chứa lớn hơn số proton
-
C.
Nguyên tử nhận thêm electron sẽ trở thành ion dương
-
D.
Nguyên tử bị mất electron sẽ trở thành ion âm
Đặt 2 điện tích \({q_1}\) và \({q_2}\) trong không khí. Lực hút tĩnh điện giữa hai điện tích là \({5.10^{ - 7}}N\). Khi đưa chúng lại gần nhau thêm \(2cm\) thì lực hút là \({2.10^{ - 6}}N\). Khoảng cách ban đầu giữa chúng là
-
A.
1 cm.
-
B.
2 cm.
-
C.
3 cm.
-
D.
4 cm.
Điện trường là
-
A.
môi trường không khí quanh điện tích
-
B.
môi trường chứa các điện tích
-
C.
môi trường bao quanh điện tích, gắn với điện tích và tác dụng lực điện lên các điện tích đặt trong nó
-
D.
môi trường dẫn điện
Các hình vẽ biểu diễn véc tơ cường độ điện trường tại điểm M trong điện trường của điện tích . Chỉ ra các hình vẽ sai
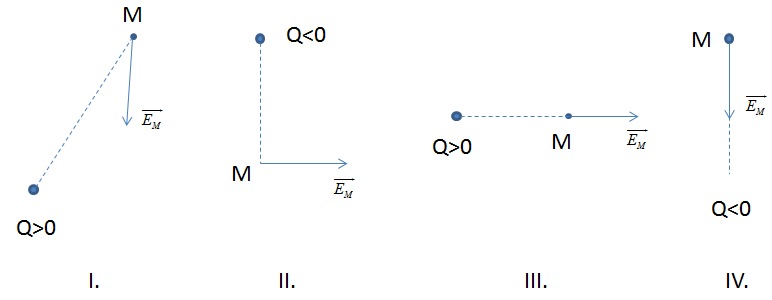
-
A.
I và II
-
B.
III và IV
-
C.
II và IV
-
D.
I và IV
Tại ba đỉnh của tam giác đều \(ABC\), cạnh \(a = 10cm\) có ba điện tích điểm bằng nhau và bằng \(10nC\). Hãy xác định cường độ điện trường tại trung điểm của cạnh AB.
-
A.
\(12000V/m\)
-
B.
\(36000V/m\)
-
C.
\(84000V/m\)
-
D.
\(96000V/m\)
Cho \({U_{BC}} = 400V\), \(BC = 10cm\), \(\alpha = {60^0}\), tam giác \(ABC\) vuông tại A như hình vẽ

Cường độ điện trường \(E\) có giá trị là:
-
A.
\(4618,8V/m\)
-
B.
\(4000V/m\)
-
C.
\(8000V/m\)
-
D.
\(8mV/m\)
Chọn phát biểu sai?
-
A.
Tụ điện cho dòng điện không đổi đi qua.
-
B.
Tụ điện dùng để tích và phóng điện trong mạch điện.
-
C.
Tụ tích điện trái dấu.
-
D.
Tụ điện không cho dòng điện một chiều đi qua.
Một tụ điện được tích điện bằng một hiệu điện thế \(10V\) thì năng lượng của tụ là \(10mJ\). Nếu muốn năng lượng của tụ là \(22,5mJ\) thì phải đặt vào hai đầu tụ một hiệu điện thế:
-
A.
\(15V\)
-
B.
\(7,5V\)
-
C.
\(20V\)
-
D.
\(40V\)
Một electron có động năng \({{\rm{W}}_d} = 200eV\) lúc bắt đầu đi vào điện trường đều của hai bản kim loại đặt song song tích điện trái dấu theo hướng đường sức. Hỏi hiệu điện thế giữa hai bản phải là bao nhiêu để hạt không đến được bản đối diện. Biết \(1eV = 1,{6.10^{ - 19}}J\)
-
A.
\(U > 200V\)
-
B.
\(U = 200V\)
-
C.
\(U < 200V\)
-
D.
\(U \ne 200V\)
Lời giải và đáp án
Biểu thức nào sau đây xác định công của lực điện?
-
A.
A = qUd
-
B.
A = qEd
-
C.
A = qE
-
D.
\(A = \frac{{qE}}{d}\)
Đáp án : B
Công của lực điện được xác định bởi biểu thức: A = qEd
Hai điện tích điểm q1 = +3 (µC) và q2 = -3 (µC), đặt trong dầu (ε = 2) cách nhau một khoảng r = 3 (cm). Lực tương tác giữa hai điện tích đó là:
-
A.
lực hút với độ lớn F = 45 (N).
-
B.
lực đẩy với độ lớn F = 45 (N).
-
C.
lực hút với độ lớn F = 90 (N).
-
D.
lực đẩy với độ lớn F = 90 (N).
Đáp án : A
Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
Ta có, q1.q2 < 0 => lực tương tác giữa hai điện tích là lực hút
Theo định luật Cu-lông, ta có:
\(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = {9.10^9}\dfrac{{\left| {{{3.10}^{ - 6}}.( - {{3.10}^{ - 6}})} \right|}}{{2.{{(0,03)}^2}}} = 45N\)
Nguyên tử trung hòa về điện, khi mất bớt electron sẽ trở thành:
-
A.
Ion-
-
B.
Ion+
-
C.
Không xác định được
-
D.
Không có gì thay đổi
Đáp án : B
Nguyên tử trung hòa về điện mà mất electron → trở thành ion +
Ta tích điện cho tụ bằng cách:
-
A.
Nối tụ với nguồn xoay chiều
-
B.
Nối tụ với nguồn pin một chiều
-
C.
Nối tụ với nguồn xoay chiều hoặc nguồn một chiều
-
D.
Không tích được điện cho tụ
Đáp án : B
Tụ điện được tích điện bằng cách nối tụ với nguồn pin một chiều
Xét các trường hợp sau với quả cầu B đang trung hòa điện:
I- Quả cầu A mang điện dương đặt gần quả cầu B bằng sắt
II- Quả cầu A mang điện dương đặt gần quả cầu B bằng sứ
III- Quả cầu A mang điện âm đặt gần quả cầu B bằng thủy tinh
IV- Quả cầu A mang điện âm đặt gần quả cầu B bằng đồng
Những trường hợp nào trên đây có sự nhiễm điện của quả cầu B
-
A.
I và III
-
B.
III và IV
-
C.
II và IV
-
D.
I và IV
Đáp án : D
Ta có:
+ Sứ và thủy tinh là chất cách điện
+ Đồng và sắt là chất dẫn điện
Quả cầu B làm bằng chất dẫn điện (sắt,đồng) sẽ bị nhiễm điện do hưởng ứng
Có hai điện tích ${q_1} = {\rm{ }}q{\rm{ }} < {\rm{ }}0$ và ${q_2} = {\rm{ }}4q$ đặt cố định trong không khí cách nhau một khoảng $a{\rm{ }} = {\rm{ }}30cm$. Phải đặt một điện tích ${q_3}$ cách ${q_1}$ một khoảng $l$ bao nhiêu để nó cân bằng?
-
A.
$l = 10cm$
-
B.
$l = 20cm$
-
C.
$l = 15cm$
-
D.
$l = 35cm$
Đáp án : A
+ Áp dụng biểu thức định luật Cu-lông: $F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}$
+ Vận dụng phương pháp tổng hợp lực
+ Vận dụng điều kiện cân bằng của vật
- Gọi:
+ A, B, C lần lượt là các điểm đặt q1, q2, q3
+ \(\overrightarrow {{F_{10}}} ,\overrightarrow {{F_{20}}} \) lần lượt là lực do q1, q2 tác dụng lên q3
- Điều kiện cân bằng của q0: \(\overrightarrow {{F_{10}}} + \overrightarrow {{F_{20}}} = 0 \to \overrightarrow {{F_{10}}} = - \overrightarrow {{F_{20}}} \)
- Vì ${q_1}$ và ${q_2}$ cùng dấu => ${q_3}$ phải nằm trong AB
=> Điểm C phải thuộc AB
Lại có:
\(\begin{array}{l}{F_{10}} = {F_{20}} \to k\dfrac{{{q_1}{q_0}}}{{C{A^2}}} = k\dfrac{{{q_2}{q_0}}}{{C{B^2}}}\\ \leftrightarrow \dfrac{{{q_1}}}{{C{A^2}}} = \dfrac{{{q_2}}}{{C{B^2}}}\\ \to \dfrac{{CB}}{{CA}} = 2\\ \to CB = 2CA\end{array}\)

Lại có: $CA{\rm{ }} + {\rm{ }}CB{\rm{ }} = {\rm{ }}30cm$
=> $CA{\rm{ }} = {\rm{ }}10cm$ và $CB{\rm{ }} = {\rm{ }}20cm$
Điện tích điểm là:
-
A.
Một vật tích điện có kích thước nhỏ so với khoảng cách điểm mà ta đang xét
-
B.
Một vật tích điện có kích thước rất lớn so với khoảng cách điểm mà ta đang xét
-
C.
Một vật tích điện có kích thước lớn so với khoảng cách điểm mà ta đang xét
-
D.
Một vật tích điện có kích thước rất nhỏ so với khoảng cách điểm mà ta đang xét
Đáp án : D
Điện tích điểm là một vật tích điện có kích thước rất nhỏ so với khoảng cách điểm mà ta đang xét
Hai điện tích q1 = 8. 10-8 C, q2 = -8. 10-8 C đặt tại A và B trong không khí biết AB = 4 cm. Tìm vectơ cường độ điện trường tại C trên đường trung trực của AB và cách AB 2 cm?
-
A.
18.105 V/m
-
B.
9.105 V/m
-
C.
12,73.105 V/m
-
D.
0 V/m
Đáp án : C
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\frac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
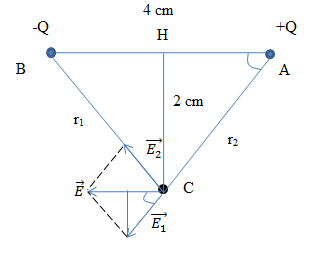
- Ta có: r1 = r2 = \(r = \sqrt {A{H^2} + A{C^2}} = 2\sqrt 2 \) cm Vì |q1| = |q2| và r1 = r2 => E1 = E2
- Từ hình vẽ ta có: \(E = 2{E_1}c{\rm{os}}\alpha \)
Với
\(\cos \alpha = \frac{{AH}}{{AC}} = \frac{2}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) => \(E = 2{E_1}\frac{{\sqrt 2 }}{2} = {E_1}\sqrt 2 \)
Ta có:
\({E_1} = k\frac{{\left| {{q_2}} \right|}}{{\varepsilon .{r_1}^2}} = {9.10^9}\frac{{\left| {{{8.10}^{ - 8}}} \right|}}{{1.{{(2.\sqrt 2 {{.10}^{ - 2}})}^2}}} = {9.10^5}V/m\)
=> E ≈ 12,73. 105 V/m.
Có 3 điện tích điểm q1 = 15.10-9C; q2 = -12.10-9C; q3 = 7.10-9C đặt tại ba đỉnh của tam giác đều ABC, cạnh 10cm. Điện thế tại tâm O và H - chân đường cao từ A xuống BC do ba điện tích gây ra là?
-
A.
V0 = 15,58V; VH = 658,8V
-
B.
V0 = 658,8V; VH = 658,8V
-
C.
V0 = 1558,8V; VH = 658,8V
-
D.
V0 = 658,8V; VH = 1658,8V
Đáp án : C
Áp dụng biểu thức tính điện thế: \({V_M} = \frac{{{A_{M\infty }}}}{q} = k\frac{Q}{r}\)
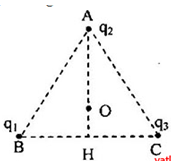
- Điện thế tại O:
\({V_0} = {V_{10}} + {V_{20}} + {V_{30}} = k\frac{{{q_1}}}{{OA}} + k\frac{{{q_2}}}{{OB}} + \frac{{{q_3}}}{{OC}}\)
Ta có, tam giác ABC đều
\( = > OA = OB = OC = \frac{2}{3}\frac{{10\sqrt 3 }}{2} = \frac{{10}}{{\sqrt 3 }}cm = \frac{{0,1}}{{\sqrt 3 }}m\)
\( \to {V_0} = \frac{k}{{OA}}({q_1} + {q_2} + {q_3}) = \frac{{{{9.10}^9}}}{{\frac{{0,1}}{{\sqrt 3 }}}}({15.10^{ - 9}} - {12.10^{ - 9}} + {7.10^{ - 9}}) = 1558,8(V)\)
- Điện thế tại H do các điện tích điểm gây ra là:
\({V_H} = {V_{1H}} + {V_{2H}} + {V_{3H}} = k\frac{{{q_1}}}{{AH}} + k\frac{{{q_2}}}{{BH}} + \frac{{{q_3}}}{{CH}}\)
Ta có: \(\left\{ \begin{array}{l}AH = \frac{{10\sqrt 3 }}{2}cm = 0,05\sqrt 3 m\\HB = HC = 5cm = 0,05m\end{array} \right.\)
\({V_H} = {9.10^9}(\frac{{{{15.10}^{ - 9}}}}{{0,05\sqrt 3 }} + \frac{{ - {{12.10}^{ - 9}}}}{{0,05}} + \frac{{{{7.10}^{ - 9}}}}{{0,05}}) = 658,8V\)
Một điện tích q chuyển động trong điện trường không đều theo một đường cong kín. Gọi công của lực điện trong chuyển động đó là A thì
-
A.
A ≥ 0 nếu q > 0.
-
B.
A > 0 nếu q < 0.
-
C.
A = 0 trong mọi trường hợp.
-
D.
A ≠ 0 còn dấu của A chưa xác định vì chưa biết chiều chuyển động của q.
Đáp án : C
Ta có công của lực điện không phụ thuộc dạng đường đi mà chỉ phụ thuộc vào điểm đầu và điểm cuối của đường đi trong điện trường
Do đó với một đường cong kín thì điểm đầu và điểm cuối trùng nhau
=> Công của lực điện trong chuyển động này bằng 0 trong mọi trường hợp
Cho các yếu tố sau:
I- Độ lớn của các điện tích
II- Dấu của các điện tích
III- Bản chất của điện môi
IV- Khoảng cách giữa hai điện tích
Độ lớn của lực tương tác giữa hai điện tích điểm đứng yên trong môi trường điện môi đồng chất phụ thuộc vào những yếu tố nào sau đây?
-
A.
II và III
-
B.
I, II và III
-
C.
I, III và IV
-
D.
Cả bốn yếu tố
Đáp án : C
Vận dụng biểu thức xác định lực tương tác của các điện tích trong điện môi: $F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}$
Ta có, biểu thức của định luật Cu-lông: $F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}$
=> Độ lớn của lực tương tác giữa hai điện tích điểm đứng yên trong môi trường điện môi đồng chất phụ thuộc vào:
+ Độ lớn của các điện tích (q1, q2)
+ Bản chất của điện môi (ε)
+ Khoảng cách giữa hai điện tích (r)
Một điện tích q = 4.10-8C di chuyển trong một điện trường đều có cường độ E = 100V/m theo một đường gấp khúc ABC, đoạn AB = 20cm và véctơ độ dời \(\overrightarrow {AB} \) làm với đường sức điện một góc 300. Đoạn BC dài 40cm và véctơ độ dời \(\overrightarrow {BC} \)làm với đường sức điện một góc 1200 . Công của lực điện bằng:
-
A.
-1,07.10-7 J
-
B.
1,07.10-7 J
-
C.
2,4.10-6 J
-
D.
-8.10-7 J
Đáp án : A
Áp dụng công thức tính công của lực điện: A = qEd
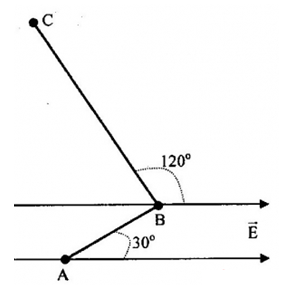
Từ hình, ta có:
\(\left\{ \begin{array}{l}{d_{AB}} = ABc{\rm{os3}}{{\rm{0}}^0} = 20.\frac{{\sqrt 3 }}{2} = 10\sqrt 3 cm\\{d_{BC}} = BCc{\rm{os12}}{{\rm{0}}^0} = 40.\left( { - \frac{1}{2}} \right) = - 20cm\end{array} \right.\)
Công của lực điện khi làm điện tích q di chuyển theo đường gấp khúc ABC là:
\(\begin{array}{l}A = {A_{AB}} + {A_{BC}} = qE\left( {{d_{AB}} + {d_{BC}}} \right)\\ = {4.10^{ - 8}}.100(0,1\sqrt 3 + ( - 0,2))\\ = - 1,{07.10^{ - 7}}J\end{array}\)
Bốn tụ điện như nhau, mỗi tụ có điện dung \(C\) được ghép song song với nhau. Điện dung của bộ tụ điện đó bằng:
-
A.
\(4C\)
-
B.
\(2C\)
-
C.
\(0,5C\)
-
D.
\(0,25C\)
Đáp án : A
Sử dụng biểu thức tính điện dung của tụ mắc song song: $C = {C_1} + {C_2} + ... + {C_n}$
Điện dung của bộ bốn tụ ghép song song với nhau là: \({C_b} = C + C + C + C = 4C\)
Cho \({q_1} = {3.10^{ - 10}}C,{\rm{ }}{q_2} = - {3.10^{ - 10}}C\), đặt tại A và B trong dầu có \(\varepsilon = 2\) biết \(AB = 2{\rm{ }}cm\) . Xác định vectơ \(\vec E\) tại điểm \(H\) - là trung điểm của \(AB\).
-
A.
\({27.10^3}V/m\)
-
B.
\({13,5.10^3}V/m\)
-
C.
\(0{\rm{ }}V/m\)
-
D.
\({36.10^5}V/m\)
Đáp án : A
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
- Gọi cường độ điện trường do \({q_1}\) gây ra là $E_1$; do $q_2$ gây ra là $E_2$
- Theo nguyên lí chồng chất điện trường:\(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
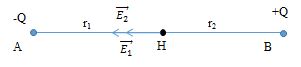
Vì \({E_1},{\rm{ }}{E_2}\) là 2 véc tơ cùng phương, cùng chiều nên: \(E{\rm{ }} = {\rm{ }}{E_1} + {\rm{ }}{E_2}\)
Ta có, cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Thay \({q_1} = {3.10^{ - 10}}C,{\rm{ }}{q_2} = - {3.10^{ - 10}}C,{\rm{ }}{r_1} = {\rm{ }}{r_2} = 1cm{\rm{ }},\varepsilon = 2\)
Ta có:
\( \to E = 2.{E_1} = 27.{\rm{ }}{10^3}V/m\)
Một con lắc đơn gồm một quả cầu tích điện dương khối lượng \(\sqrt 3 g\) buộc vào sợi dây mảnh cách điện. Con lắc treo trong điện trường đều có phương nằm ngang với cường độ điện trường \(10000{\rm{ }}V/m\). Tại nơi có \(g = 9,8m/{s^2}\). Khi vật ở vị trí cân bằng, sợi dây lệch một góc \(\alpha = {\rm{ }}{30^0}\) so với phương thẳng đứng. Độ lớn của điện tích của quả cầu là:
-
A.
\({4.10^{ - 7}}C\)
-
B.
\({3,27.10^{ - 7}}C\)
-
C.
\({9,8.10^{ - 7}}C\)
-
D.
\({10^{ - 7}}C\)
Đáp án : C
+ Xác định các lực tác dụng lên vật
+ Áp dụng điều kiện cân bằng của vật
+ Áp dụng biểu thức tính lực điện: \(F{\rm{ }} = {\rm{ }}qE\)
+ Vận dụng công thức lượng giác.
Các lực tác dụng lên quả cầu gồm: lực điện \(\overrightarrow F \) , trọng lực \(\overrightarrow P \)hướng xuống và lực căng dây \(\overrightarrow T \).
Khi quả cầu cân bằng: \(\overrightarrow T + \overrightarrow P + \overrightarrow F = 0 \to \overrightarrow T + \overrightarrow {P'} = 0\)
=> $P'$ có phương sợi dây $P'$ tạo với $P$ một góc \(\alpha {\rm{ }} = {\rm{ }}{30^0}\)
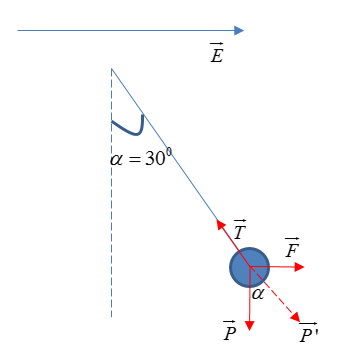
Từ hình ta có: \(\tan \alpha = \dfrac{F}{P} = \dfrac{{\left| q \right|E}}{{mg}} = \tan {30^0} \to \left| q \right| = \dfrac{{mg\tan {{30}^0}}}{E} = \dfrac{{\sqrt 3 {{.10}^{ - 3}}.9,8.\tan {{30}^0}}}{{10000}} = {9,8.10^{ - 7}}C\)
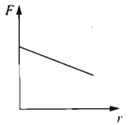
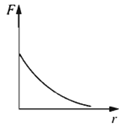
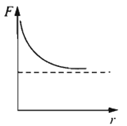
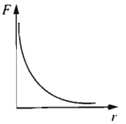
Đồ thị nào trong các đồ thị dưới đây có thể biểu diễn sự phụ thuộc của lực tương tác giữa hai điện tích điểm vào khoảng cách giữa chúng?
-
A.

-
B.

-
C.

-
D.

Đáp án : D
Vận dụng biểu thức tính lực tương tác giữa hai điện tích điểm: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)
Ta có, lực tương tác giữa hai điện tích điểm: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\) hay \(F = \dfrac{A}{{{r^2}}}\)
=> Đồ thị \(F\left( r \right)\) có dạng đường hypebol (đồ thị D: Khi r tiến đến 0 thì F tiến tới \(\infty \), khi r tiến đến \(\infty \) thì F tiến tới 0)
Theo nội dung của thuyết electron, phát biểu nào sau đây là đúng?
-
A.
Electron không thể rời khỏi nguyên tử để di chuyển từ nơi này đến nơi khác
-
B.
Vật nhiễm điện âm khi chỉ số electron mà nó chứa lớn hơn số proton
-
C.
Nguyên tử nhận thêm electron sẽ trở thành ion dương
-
D.
Nguyên tử bị mất electron sẽ trở thành ion âm
Đáp án : B
A – sai vì: Electron có thể rời khỏi nguyên tử để di chuyển từ nơi này đến nơi khác
B - đúng
C - sai vì: Nguyên tử nhận thêm electron sẽ trở thành ion âm
D – sai vì: Nguyên tử bị mất electron sẽ trở thành ion dương
Đặt 2 điện tích \({q_1}\) và \({q_2}\) trong không khí. Lực hút tĩnh điện giữa hai điện tích là \({5.10^{ - 7}}N\). Khi đưa chúng lại gần nhau thêm \(2cm\) thì lực hút là \({2.10^{ - 6}}N\). Khoảng cách ban đầu giữa chúng là
-
A.
1 cm.
-
B.
2 cm.
-
C.
3 cm.
-
D.
4 cm.
Đáp án : D
Áp dụng biểu thức tính lực tương tác tĩnh điện: \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)
Ta có:
+ Khi khoảng cách giữa hai điện tích \(r\): \(F = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} = {5.10^{ - 7}}N\)
+ Khi đưa chúng ra lại gần nhau thêm \(2cm\) thì khoảng cách giữa hai điện tích lúc này là \(r' = r - 0,02\), khi đó:
\(F' = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{r{'^2}}} = k\dfrac{{\left| {{q_1}{q_2}} \right|}}{{{{(r - 0,02)}^2}}} = {2.10^{ - 6}}N\)
\(\begin{array}{l} \to \dfrac{F}{{F'}} = \dfrac{{r{'^2}}}{{{r^2}}} = \dfrac{{{{(r - 0,02)}^2}}}{{{r^2}}} = \dfrac{{{{5.10}^{ - 7}}}}{{{{2.10}^{ - 6}}}} = \dfrac{1}{4}\\ \to r - 0,02 = \dfrac{{\rm{r}}}{2}\\ \to r = 0,04m = 4cm\end{array}\)
Điện trường là
-
A.
môi trường không khí quanh điện tích
-
B.
môi trường chứa các điện tích
-
C.
môi trường bao quanh điện tích, gắn với điện tích và tác dụng lực điện lên các điện tích đặt trong nó
-
D.
môi trường dẫn điện
Đáp án : C
Ta có: Điện trường là một dạng vật chất bao quanh các điện tích và truyền tương tác điện
=> Phương án C đúng
Các hình vẽ biểu diễn véc tơ cường độ điện trường tại điểm M trong điện trường của điện tích . Chỉ ra các hình vẽ sai

-
A.
I và II
-
B.
III và IV
-
C.
II và IV
-
D.
I và IV
Đáp án : A
Ta có, véc-tơ cường độ điện trường có:
+ Điểm đặt: Đặt tại điểm đang xét
+ Phương: Là đường thẳng nối giữa điện tích Q với điểm ta đang xét
+ Chiều:
- Nếu Q > 0: E hướng ra xa +Q
- Nếu Q < 0: E hướng vào –Q
Từ đó ta suy ra biểu diễn véc tơ cường độ điện trường tại điểm M trong điện trường của điện tích \(Q\) trong hình I và hình II là sai.
Tại ba đỉnh của tam giác đều \(ABC\), cạnh \(a = 10cm\) có ba điện tích điểm bằng nhau và bằng \(10nC\). Hãy xác định cường độ điện trường tại trung điểm của cạnh AB.
-
A.
\(12000V/m\)
-
B.
\(36000V/m\)
-
C.
\(84000V/m\)
-
D.
\(96000V/m\)
Đáp án : A
+ Áp dụng nguyên lí chồng chất điện trường: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + ... + \overrightarrow {{E_n}} \)
+ Áp dụng biểu thức xác định cường độ điện trường: \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)
Gọi \(H\) - trung điểm của cạnh \(AB\)
Gọi \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) lần lượt là cường độ điện trường do điện tích \({q_1},{q_2},{q_3}\) gây ra tại \(H\)
Ta có, các véc-tơ \(\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) được biểu diễn như hình
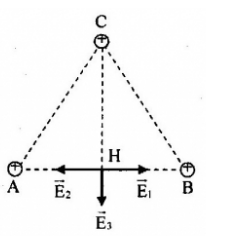
Ta có: \({E_1} = {E_2} = k\dfrac{{\left| q \right|}}{{{{\left( {\dfrac{{AB}}{2}} \right)}^2}}}\)
\({E_3} = k\dfrac{{\left| q \right|}}{{C{H^2}}}\)
Lại có:
\(\begin{array}{l}CH = \sqrt {C{B^2} - B{H^2}} = \sqrt {C{B^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}} \\ = \sqrt {{{10}^2} - \dfrac{{{{10}^2}}}{4}} = 5\sqrt 3 cm\end{array}\)
Ta suy ra: \({E_3} = {9.10^9}\dfrac{{{{10.10}^{ - 9}}}}{{{{\left( {5\sqrt 3 {{.10}^{ - 2}}} \right)}^2}}} = 12000V/m\)
Ta có, cường độ điện trường tổng hợp tại \(H\): \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} \)
Vì \(\left\{ \begin{array}{l}\overrightarrow {{E_1}} \uparrow \downarrow \overrightarrow {{E_2}} \\{E_1} = {E_2}\end{array} \right. \Rightarrow \overrightarrow {{E_{12}}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} = \overrightarrow 0 \)
Ta suy ra: \(\overrightarrow E = \overrightarrow {{E_3}} \)
\( \Rightarrow E = {E_3} = 12000V/m\)
Cho \({U_{BC}} = 400V\), \(BC = 10cm\), \(\alpha = {60^0}\), tam giác \(ABC\) vuông tại A như hình vẽ

Cường độ điện trường \(E\) có giá trị là:
-
A.
\(4618,8V/m\)
-
B.
\(4000V/m\)
-
C.
\(8000V/m\)
-
D.
\(8mV/m\)
Đáp án : C
Áp dụng biểu thức mối liên hệ giữa cường độ điện trường và hiệu điện thế: \(E = \dfrac{U}{d}\)
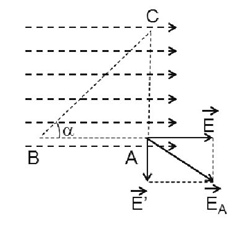
Ta có,
+ \({U_{AC}} = \dfrac{{{A_{AC}}}}{q} = E.AC.cos{90^0} = 0V\)
+ \({U_{BA}} = {U_{BC}} + {U_{CA}} = {U_{BC}} = 400V\)
Cường độ điện trường: \(E = \dfrac{{{U_{BC}}}}{{BC\cos \alpha }} = \dfrac{{400}}{{0,1.cos{{60}^0}}} = 8000V/m\)
Chọn phát biểu sai?
-
A.
Tụ điện cho dòng điện không đổi đi qua.
-
B.
Tụ điện dùng để tích và phóng điện trong mạch điện.
-
C.
Tụ tích điện trái dấu.
-
D.
Tụ điện không cho dòng điện một chiều đi qua.
Đáp án : A
A – sai vì: Tụ điện không cho dòng điện không đổi đi qua
B, C, D - đúng
Một tụ điện được tích điện bằng một hiệu điện thế \(10V\) thì năng lượng của tụ là \(10mJ\). Nếu muốn năng lượng của tụ là \(22,5mJ\) thì phải đặt vào hai đầu tụ một hiệu điện thế:
-
A.
\(15V\)
-
B.
\(7,5V\)
-
C.
\(20V\)
-
D.
\(40V\)
Đáp án : A
Vận dụng biểu thức tính năng lượng điện trường: \({\rm{W}} = \dfrac{1}{2}C{U^2}\)
Ta có:
+ Khi \({U_1} = 10V\) thì \({{\rm{W}}_1} = \dfrac{1}{2}CU_1^2 = 10mJ\) (1)
+ Khi \({U_2} = ?\) thì \({{\rm{W}}_2} = \dfrac{1}{2}CU_2^2 = 22,5mJ\) (2)
Lấy \(\dfrac{{\left( 2 \right)}}{{\left( 1 \right)}}\) ta được:
\(\begin{array}{l}\dfrac{{{{\rm{W}}_2}}}{{{{\rm{W}}_1}}} = \dfrac{{U_2^2}}{{U_1^2}} \Leftrightarrow \dfrac{{22,5}}{{10}} = \dfrac{{U_2^2}}{{{{10}^2}}}\\ \Rightarrow {U_2} = 15V\end{array}\)
Một electron có động năng \({{\rm{W}}_d} = 200eV\) lúc bắt đầu đi vào điện trường đều của hai bản kim loại đặt song song tích điện trái dấu theo hướng đường sức. Hỏi hiệu điện thế giữa hai bản phải là bao nhiêu để hạt không đến được bản đối diện. Biết \(1eV = 1,{6.10^{ - 19}}J\)
-
A.
\(U > 200V\)
-
B.
\(U = 200V\)
-
C.
\(U < 200V\)
-
D.
\(U \ne 200V\)
Đáp án : A
+ Sử dụng định lí biến thiên động năng: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = {A_{ngoailuc}}\)
+ Sử dụng biểu thức liên hệ giữa cường độ điện trường và hiệu điện thế: \(E = \dfrac{U}{d}\)
Khi electron chuyển động từ bản này đến bản kia, thì nó chịu tác dụng của ngoại lực là lực điện trường.
+ Theo định lí động năng, ta có: \({{\rm{W}}_{{d_2}}} - {{\rm{W}}_{{d_1}}} = qE{d_{12}}\)
\( \Rightarrow {d_{12}} = \dfrac{{ - {{\rm{W}}_{{d_1}}}}}{{qE}} = \dfrac{{ - 200.1,{{6.10}^{ - 19}}}}{{ - 1,{{6.10}^{ - 19}}.E}} = \dfrac{{200}}{E}\)
+ Để electron không đến được bản đối diện thì quãng đường nó đi được phải nhỏ hơn khoảng cách giữa hai bản này hay \({d_{12}} < d\) (1)
Lại có: \(d = \dfrac{U}{E}\) (2)
Từ (1) và (2) ta suy ra: \(\dfrac{{200}}{E} < \dfrac{U}{E} \Rightarrow U > 200V\)
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận