Đề kiểm tra 1 tiết chương 2: Dòng điện không đổi - Đề số 03
Đề bài
Dòng điện là:
-
A.
dòng dịch chuyển của điện tích
-
B.
dòng dịch chuyển có hướng của các điện tích tự do
-
C.
dòng dịch chuyển của các điện tích tự do
-
D.
dòng dịch chuyển có hướng của các ion dương và âm
Biểu thức xác định định luật Ôm cho đoạn mạch chỉ có điện trở?
-
A.
\(I = \frac{U}{R}\)
-
B.
\(I = U{\rm{R}}\)
-
C.
\(I = \frac{R}{U}\)
-
D.
\(I = {U^R}\)
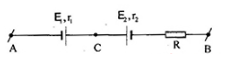
Cho mạch điện như hình vẽ:
\({E_1} = 8V\), \({r_1} = 1,2\Omega \), \({E_2} = 4V\), \({r_2} = 0,4\Omega \), \(R = 28,4\Omega \), \({U_{AB}} = 6V\). Cường độ dòng điện trong mạch và chiều của nó là?
-
A.
\(\dfrac{1}{3}A\), chiều từ A đến B
-
B.
\(\dfrac{1}{3}A\), chiều từ B đến A
-
C.
\(\dfrac{1}{{15}}A\), chiều từ A đến B
-
D.
\(\dfrac{1}{{15}}A\), chiều từ B đến A
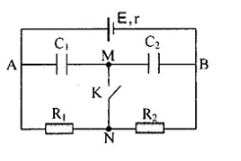
Cho mạch điện sau:
Biết E = 24V, r = 2$\Omega $, R1 = R2 = 5$\Omega $, C1 = 4.10-7F, C2 = 6.10-7F.
Điện tích trên 2 bản tụ điện khi K đóng là?
-
A.
Q1 = Q2 = 4.10-6C
-
B.
Q1 = 6.10-7C, Q2 = 4.10-6C
-
C.
Q1 = Q2 = 6.10-7C
-
D.
Q1 = 4.10-6C , Q2 = 6.10-6C
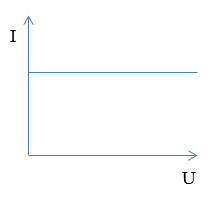
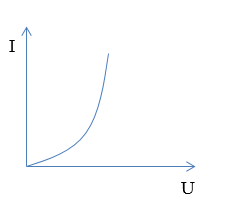
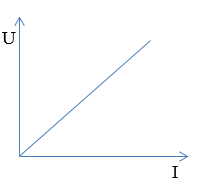
Đồ thị nào sau đây diễn tả đúng mối liên hệ giữa hiệu điện thế $(U)$ và cường độ dòng điện $(I)$ trong đoạn mạch chỉ có điện trở?
-
A.
-
B.
-
C.
-
D.
Cho đoạn mạch gồm R1 mắc nối tiếp với R2, biểu thức nào sau đây là sai ?
-
A.
R = R1 + R2
-
B.
U = U1 + U2
-
C.
I = I1 + I2
-
D.
\({I_1} = \frac{{{U_1}}}{{{R_1}}}\)
Cho mạch điện như hình vẽ:
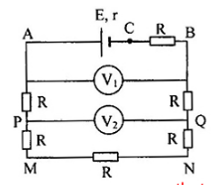
E = 24V, r = 0. Các vôn kế giống nhau. Nếu \(r = 0\) thì số chỉ vôn kế \(V_1\) là \(12V\)
Số chỉ các vôn kế V2 có giá trị là:
-
A.
2V
-
B.
8V
-
C.
6V
-
D.
4V
Một bộ nguồn có ba nguồn giống nhau mắc nối tiếp. Mạch ngoài là một điện trở không đổi. Nếu đảo hai cực của một nguồn thì
-
A.
độ giảm hiệu điện thế ở điện trở trong của bộ nguồn không đổi.
-
B.
cường độ dòng điện trong mạch giảm đi hai lần.
-
C.
hiệu điện thế giữa hai đầu điện trở mạch ngoài giảm đi ba lần.
-
D.
công suất tỏa nhiệt trên mạch ngoài giảm đi bốn lần.
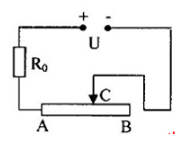
Cho mạch điện như hình vẽ.
Biến trở AB là dây đồng chất, dài l = 1,3m, tiết diện S = 0,1mm2, điện trở suất 10-6Wm, U- hiệu điện thế không đổi. Nhận thấy khi con chạy ở các vị trí cách đầu A hoặc đầu B những đoạn như nhau bằng 40cm thì công suất tỏa nhiệt trên biến trở là như nhau. Xác định R0 ứng với vị trí của C.
-
A.
3$\Omega $
-
B.
2$\Omega $
-
C.
4$\Omega $
-
D.
6$\Omega $
Cho mạch điện như hình vẽ
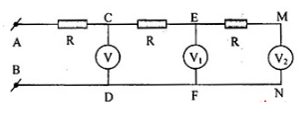
Biết 3 vôn kế giống nhau, UV = 5V, UV2 = 1V. Số chỉ của vôn kế V1 là bao nhiêu?
-
A.
0,5V
-
B.
1V
-
C.
2V
-
D.
4V
Khi dòng điện chạy qua đoạn mạch ngoài nối giữa hai cực của nguồn điện thì các hạt mang điện chuyển động có hướng dưới tác dụng của lực:
-
A.
Cu - long
-
B.
hấp dẫn
-
C.
lực lạ
-
D.
điện trường
Một bộ acquy có thể cung cấp dòng điện 4 A liên tục trong 2 giờ thì phải nạp lại. Suất điện động của acquy này nếu trong thời gian hoạt động trên đây nó sản sinh ra một công là 172,8 kJ là ?
-
A.
6V
-
B.
3V
-
C.
1,2V
-
D.
2,4V
Phát biểu nào sau đây là không đúng?
-
A.
Dòng điện có tác dụng từ. Ví dụ: nam châm điện.
-
B.
Dòng điện có tác dụng nhiệt. Ví dụ: bàn là điện.
-
C.
Dòng điện có tác dụng hoá học. Ví dụ: acquy nóng lên khi nạp điện.
-
D.
Dòng điện có tác dụng sinh lý. Ví dụ: hiện tượng điện giật.
Cho đoạn mạch gồm điện trở \({R_1} = 100\Omega \), mắc nối tiếp với điện trở \({R_2} = 200\Omega \). Đặt vào hai đầu đoạn mạch một hiệu điện thế \(U\) khi đó hiệu điên thế giữa hai đầu điện trở \({R_1}\) là \(6{\rm{ }}\left( V \right)\). Hiệu điện thế giữa hai đầu đoạn mạch là:
-
A.
\(U{\rm{ }} = {\rm{ }}12{\rm{ }}\left( V \right)\)
-
B.
\(U{\rm{ }} = {\rm{ }}6{\rm{ }}\left( V \right)\)
-
C.
\(U{\rm{ }} = {\rm{ }}18{\rm{ }}\left( V \right)\)
-
D.
\(U{\rm{ }} = {\rm{ }}24{\rm{ }}\left( V \right)\)
Biểu thức định luật Ôm cho toàn mạch trong trường hợp mạch ngoài chứa máy thu là:
-
A.
\(I = \frac{U}{R}\)
-
B.
\(I = \frac{E}{{R + r}}\)
-
C.
\(I = \frac{{E - {E_p}}}{{R + r + r'}}\)
-
D.
\(I = \frac{{{U_{AB}} + E}}{{{R_{AB}}}}\)
Một pin có suất điện động 1,5V và điện trở trong là \(0,5\Omega \). Mắc một bóng đèn có điện trở \(2,5\Omega \) vào hai cực của pin này thành mạch điện kín. Cường độ dòng điện chạy qua đèn là
-
A.
2A
-
B.
1A
-
C.
1,5A
-
D.
0,5A
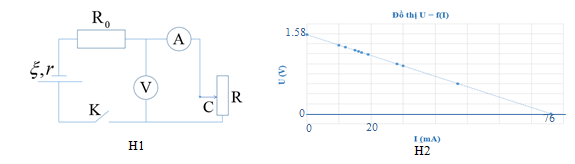
Để xác định điện trở trong r của một nguồn điện, một học sinh mắc mạch điện như hình (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của số chỉ U của vôn kế V vào số chỉ I của ampe kế A như hình (H2). Điện trở của vôn kế rất lớn. Biết \({R_0} = 2{\rm{0,3 \Omega }}\). Giá trị của r được xác định bởi thí nghiệm này là
-
A.
\({\rm{0,49 \Omega }}\)
-
B.
\({\rm{0,85 \Omega }}\)
-
C.
\({\rm{1,0 \Omega }}\)
-
D.
\({\rm{1,5 \Omega }}\)
Dấu hiệu tổng quát nhất để nhận biết dòng điện là:
-
A.
tác dụng hóa học.
-
B.
tác dụng từ.
-
C.
tác dụng nhiệt.
-
D.
tác dụng sinh lí.
Biểu thức nào sau đây là đúng
-
A.
\(q = \dfrac{I}{t}\)
-
B.
\(I = \dfrac{t}{q}\)
-
C.
\(q = {I^t}\)
-
D.
\(I = \dfrac{q}{t}\)
Điện tích của electron là \( - {1,6.10^{ - 19}}C\), điện lượng chuyển qua tiết diện thẳng của dây dẫn trong \(30s\) là \(15C\). Số electron chuyển qua tiết diện thẳng của dây dẫn trong thời gian một giây là
-
A.
\({3,125.10^{18}}\)
-
B.
\({9,375.10^{19}}\)
-
C.
\({7,895.10^{19}}\)
-
D.
\({2,632.10^{18}}\)
Chọn phương án sai.
Khi một tải R nối vào nguồn suất điện động \(\xi \) và điện trở trong r, thấy công suất mạch ngoài cực đại thì:
-
A.
\(I = \dfrac{{{E}}}{{2R}}\)
-
B.
\(r = R\)
-
C.
\({P_R} = \dfrac{{{E^2}}}{{4r}}\)
-
D.
\(I = \dfrac{\xi }{r}\)
Cho mạch điện có sơ đồ như hình vẽ:
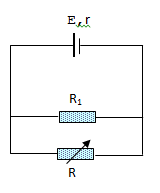
Biết, \(E = 6V,r = 1\Omega ,{R_1} = 4\Omega \), R là biến trở
Tìm R để công suất tiêu thụ trên R là cực đại? Tính giá trị công suất cực đại khi đó?
-
A.
\(R = \dfrac{3}{2}\Omega ,{P_{{\rm{max}}}} = 37,5{\rm{W}}\)
-
B.
\(R = \dfrac{2}{3}\Omega ,{P_{{\rm{max}}}} = 37,5{\rm{W}}\)
-
C.
\(R = \dfrac{4}{5}\Omega ,{P_{{\rm{max}}}} = 7,2{\rm{W}}\)
-
D.
\(R = \dfrac{5}{4}\Omega ,{P_{{\rm{max}}}} = 7,2{\rm{W}}\)
Một biến trở con chạy được làm bằng dây dẫn hợp kim Nikelin có điện trở suất \({4.10^{ - 7}}\Omega .m\), có tiết diện đầu là \(0,8m{m^2}\) và gồm \(300\) vòng cuốn quanh lõi sứ trụ tròn đường kính \(4,5cm\). Tính điện trở lớn nhất của biến trở này.
-
A.
\(21,2\Omega \)
-
B.
\(10\Omega \)
-
C.
\(15,3\Omega \)
-
D.
\(7,1\Omega \)
Đối với mạch điện kín, thì hiệu suất của nguồn điện không được tính bằng công thức:
-
A.
\(H = \dfrac{{{A_{coich}}}}{{{A_{nguon}}}}.100\% \)
-
B.
\(H = \dfrac{{{U_N}}}{E}.100\% \)
-
C.
\(H = \dfrac{{{R_N}}}{{{R_N} + r}}.100\% \)
-
D.
\(H = \dfrac{r}{{{R_N} + r}}.100\% \)
Cho 2 mạch điện như hình vẽ:
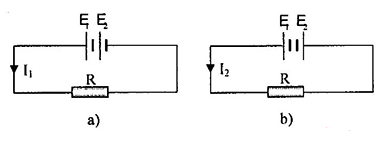
\({E_1} = 18V,{r_1} = 1\Omega \). Cho \(R = 9\Omega \), \({I_1} = 2,5A\), \({I_2} = 0,5A\). Tìm \({E_2}\) và \({r_2}\)
-
A.
\(\left\{ \begin{array}{l}{E_2} = 12V\\{r_2} = 1\Omega \end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}{E_2} = 12V\\{r_2} = 2\Omega \end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}{E_2} = 6V\\{r_2} = 1\Omega \end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}{E_2} = 6V\\{r_2} = 2\Omega \end{array} \right.\)
Lời giải và đáp án
Dòng điện là:
-
A.
dòng dịch chuyển của điện tích
-
B.
dòng dịch chuyển có hướng của các điện tích tự do
-
C.
dòng dịch chuyển của các điện tích tự do
-
D.
dòng dịch chuyển có hướng của các ion dương và âm
Đáp án : B
Dòng điện là dòng các điện tích (các hạt tải điện) dịch chuyển có hướng.
Biểu thức xác định định luật Ôm cho đoạn mạch chỉ có điện trở?
-
A.
\(I = \frac{U}{R}\)
-
B.
\(I = U{\rm{R}}\)
-
C.
\(I = \frac{R}{U}\)
-
D.
\(I = {U^R}\)
Đáp án : A
Biểu thức xác định định luật Ôm cho đoạn mạch chỉ có điện trở là: \(I = \frac{U}{R}\)
Cho mạch điện như hình vẽ:
\({E_1} = 8V\), \({r_1} = 1,2\Omega \), \({E_2} = 4V\), \({r_2} = 0,4\Omega \), \(R = 28,4\Omega \), \({U_{AB}} = 6V\). Cường độ dòng điện trong mạch và chiều của nó là?

-
A.
\(\dfrac{1}{3}A\), chiều từ A đến B
-
B.
\(\dfrac{1}{3}A\), chiều từ B đến A
-
C.
\(\dfrac{1}{{15}}A\), chiều từ A đến B
-
D.
\(\dfrac{1}{{15}}A\), chiều từ B đến A
Đáp án : A
+ Giả sử chiều dòng điện
+ Áp dụng định luật Ôm cho đoạn mạch
Giả sử dòng điện trong đoạn mạch có chiều từ A đến B.
Khi đó E1 là máy phát, E2 là máy thu.
+ Áp dụng định luật Ôm cho đoạn mạch AB, ta có:
\(I = \dfrac{{{U_{AB}} + {E_1} - {E_2}}}{{R + {r_1} + {r_2}}} = \dfrac{1}{3}A\)
Nhận thấy I > 0 => điều giả sử là đúng hay dòng điện có chiều từ A đến B
Cho mạch điện sau:
Biết E = 24V, r = 2$\Omega $, R1 = R2 = 5$\Omega $, C1 = 4.10-7F, C2 = 6.10-7F.
Điện tích trên 2 bản tụ điện khi K đóng là?

-
A.
Q1 = Q2 = 4.10-6C
-
B.
Q1 = 6.10-7C, Q2 = 4.10-6C
-
C.
Q1 = Q2 = 6.10-7C
-
D.
Q1 = 4.10-6C , Q2 = 6.10-6C
Đáp án : D
+ Áp dụng định luật Ôm cho toàn mạch: \(I = \frac{E}{{{R_N} + r}}\)
+ Áp dụng biểu thức Q = CU
Ta có: Dòng điện một chiều không qua tụ điện nên khi khóa K đóng - dòng điện chỉ chạy qua R1 và R2.
Dòng điện chạy trong mạch:
\(I = \frac{E}{{{R_1} + {R_2} + r}} = \frac{{24}}{{5 + 5 + 2}} = 2(A)\)
+ Lúc này, tụ C1 // R1 và tụ C2 // R2, ta có:
\(\left\{ \begin{array}{l}{U_{C1}} = {U_{R1}} = I{R_1} = 10V\\{U_{C2}} = {U_{R2}} = I{R_2} = 10V\end{array} \right.\)
Điện tích của các tụ lúc này:
\(\left\{ \begin{array}{l}{Q_1} = {C_1}{U_{C1}} = {4.10^{ - 6}}C\\{Q_2} = {C_2}{U_{C2}} = {6.10^{ - 6}}C\end{array} \right.\)
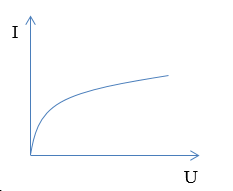
Đồ thị nào sau đây diễn tả đúng mối liên hệ giữa hiệu điện thế $(U)$ và cường độ dòng điện $(I)$ trong đoạn mạch chỉ có điện trở?
-
A.
-
B.
-
C.
-
D.
Đáp án : C
Vận dụng biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \frac{U}{R}\)
Ta có: Biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \frac{U}{R} \to U = IR\)
=> Đồ thị có dạng của hàm số y = ax
Cho đoạn mạch gồm R1 mắc nối tiếp với R2, biểu thức nào sau đây là sai ?
-
A.
R = R1 + R2
-
B.
U = U1 + U2
-
C.
I = I1 + I2
-
D.
\({I_1} = \frac{{{U_1}}}{{{R_1}}}\)
Đáp án : C
A, B, D - đúng
C - sai vì : khi R1 mắc nối tiếp với R2 thì I = I1 = I2
Cho mạch điện như hình vẽ:

E = 24V, r = 0. Các vôn kế giống nhau. Nếu \(r = 0\) thì số chỉ vôn kế \(V_1\) là \(12V\)
Số chỉ các vôn kế V2 có giá trị là:
-
A.
2V
-
B.
8V
-
C.
6V
-
D.
4V
Đáp án : D
- Giả sử RV vô cùng lớn: RV = ∞
+ Số chỉ trên V1 là: \({U_1} = 5R\dfrac{E}{{6R}} = \dfrac{5}{6}E = \dfrac{5}{6}.24 = 20V\)
Điều này trái với giả thiết => điều giả sử là sai hay RV hữu hạn.
- Ta có: UAC = 24V => UBC = 12V
\( \to {R_{CMNB}} = R \\\leftrightarrow \dfrac{{(2R + {R_{PQ}}){R_V}}}{{2R + {R_{PQ}} + {R_V}}} = R\)
Với \({R_{PQ}} = \dfrac{{3R.{R_V}}}{{3R + {R_V}}} \to {R_V} = 1,5R\)
Số chỉ trên V2 :
+ \({U_2} = \dfrac{{{U_{BC}}}}{{3R}}R = 4V\)
Một bộ nguồn có ba nguồn giống nhau mắc nối tiếp. Mạch ngoài là một điện trở không đổi. Nếu đảo hai cực của một nguồn thì
-
A.
độ giảm hiệu điện thế ở điện trở trong của bộ nguồn không đổi.
-
B.
cường độ dòng điện trong mạch giảm đi hai lần.
-
C.
hiệu điện thế giữa hai đầu điện trở mạch ngoài giảm đi ba lần.
-
D.
công suất tỏa nhiệt trên mạch ngoài giảm đi bốn lần.
Đáp án : C
Vận dụng lí thuyết về mắc nguồn xung đối
- Khi 3 nguồn mắc nối tiếp: Eb = 3E, rb = 3r
\(I = \frac{{3E}}{{R + 3{\rm{r}}}}\)
- Khi đảo hai cực của một nguồn thì:
\({E_b}' = \left| {{E_1} - {E_2}} \right| + {E_3} = E,{r_b}' = 3{\rm{r,}}I' = \frac{E}{{R + 3{\rm{r}}}}\)
Hiệu điện thế giữa hai đầu điện trở mạch ngoài: UN = I.RN
Ta thấy cường độ dòng điện giảm 3 lần
=> Hiệu điện thế giữa hai đầu điện trở mạch ngoài giảm đi 3 lần
Cho mạch điện như hình vẽ.
Biến trở AB là dây đồng chất, dài l = 1,3m, tiết diện S = 0,1mm2, điện trở suất 10-6Wm, U- hiệu điện thế không đổi. Nhận thấy khi con chạy ở các vị trí cách đầu A hoặc đầu B những đoạn như nhau bằng 40cm thì công suất tỏa nhiệt trên biến trở là như nhau. Xác định R0 ứng với vị trí của C.

-
A.
3$\Omega $
-
B.
2$\Omega $
-
C.
4$\Omega $
-
D.
6$\Omega $
Đáp án : D
+ Áp dụng biểu thức xác định điện trở của dây dẫn: \(R = \rho \frac{l}{S}\)
Gọi R1, R2 là điện trở của biến trở ứng với 2 vị trí trên của con chạyC; R là điện trở toàn phần của biến trở.
+ Điện trở toàn phần của biến trở:
\(R = \rho \frac{l}{S} = 13\Omega \to \left\{ \begin{array}{l}{R_1} = \frac{4}{{13}}R = 4\Omega \\{R_2} = \frac{9}{{13}}R = 9\Omega \end{array} \right.\)
+ Ta có:
\(\begin{array}{l}{P_1} = {P_2} \leftrightarrow {\left( {\frac{U}{{{R_0} + {R_1}}}} \right)^2}{R_1} = {\left( {\frac{U}{{{R_0} + {R_2}}}} \right)^2}{R_2}\\ \to {R_0} = \sqrt {{R_1}{R_2}} = 6\Omega \end{array}\)
Cho mạch điện như hình vẽ

Biết 3 vôn kế giống nhau, UV = 5V, UV2 = 1V. Số chỉ của vôn kế V1 là bao nhiêu?
-
A.
0,5V
-
B.
1V
-
C.
2V
-
D.
4V
Đáp án : C
+ Áp dụng biểu thức xác định điện trở trong mạch nối tiếp: R = R1 + R2 + .... + Rn
+ Áp dụng biểu thức xác định điện trở trong mạch song song:
\(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}\)
Giả sử các vôn kế có điện trở vô cùng lớn, khi đó mạch chỉ gồm các điện trở nối tiếp.
Ta có:
\(\left\{ \begin{array}{l}{U_{CD}} = V = I.2R\\{U_{MN}} = {V_2} = 0\end{array} \right.\)
=> Vôn kế có điện trở RV không phải rất lớn so với R.
+ Xét đoạn mạch MN:
\({I_{V2}}{R_V} = {\rm{ }}1 \to {I_{V2}} = \dfrac{1}{{{R_V}}}\)
+ Xét đoạn mạch EF:
\(\begin{array}{l}{U_{EF}} = {I_{V1}}{R_V} = {I_{V2}}R + {U_{MN}} \\= {I_{V2}}R + 1 = \dfrac{R}{{{R_V}}} + 1\\ \to {I_{V1}} = \dfrac{R}{{R_V^2}} + \dfrac{1}{{{R_V}}}\end{array}\)
+ Xét đoạn mạch CD:
\(\begin{array}{l}{U_{CD}} = {I_1}R + {U_{EF}} \\= {I_1}R + \dfrac{R}{{{R_V}}} + 1 = 5\\ \leftrightarrow {I_1}R + \dfrac{R}{{{R_V}}} = 4 \\\leftrightarrow ({I_{V1}} + {I_{V2}})R + \dfrac{R}{{{R_V}}} = 4\\ \leftrightarrow \left( {\dfrac{R}{{R_V^2}} + \dfrac{1}{{{R_V}}} + \dfrac{1}{{{R_V}}}} \right)R + \dfrac{R}{{{R_V}}} = 4 \\\leftrightarrow \dfrac{{{R^2}}}{{R_V^2}} + \dfrac{{3R}}{{{R_V}}} = 4\\ \leftrightarrow {R^2} + 3{\rm{R}}{{\rm{R}}_V} - 4{\rm{R}}_V^2 = 0\\ \to R = {R_V}\end{array}\)
Vậy
\({U_{EF}} = {\rm{ }}{I_{V1}}{R_V} = {\rm{ }}{I_{V2}}R{\rm{ }} + {\rm{ }}{U_{MN}} \\= \dfrac{R}{{{R_V}}}{\rm{ }} + {\rm{ }}1 = 2V\)
Khi dòng điện chạy qua đoạn mạch ngoài nối giữa hai cực của nguồn điện thì các hạt mang điện chuyển động có hướng dưới tác dụng của lực:
-
A.
Cu - long
-
B.
hấp dẫn
-
C.
lực lạ
-
D.
điện trường
Đáp án : D
+ Sử dụng lí thuyết về các loại lực
+ Sử dụng lí thuyết về chuyển động của hạt mang điện
Khi có dòng điện chạy qua đoạn mạch ngoài nối giữa hai cực của nguồn điện thì các hạt mang điện chuyển động có hướng dưới tác dụng của lực điện trường.
Cụ thể: Các hạt mang điện tích dương chuyển động theo chiều điện trường, các hạt mang điện tích âm chuyển động ngược chiều điện trường.
Một bộ acquy có thể cung cấp dòng điện 4 A liên tục trong 2 giờ thì phải nạp lại. Suất điện động của acquy này nếu trong thời gian hoạt động trên đây nó sản sinh ra một công là 172,8 kJ là ?
-
A.
6V
-
B.
3V
-
C.
1,2V
-
D.
2,4V
Đáp án : A
Vận dụng biểu thức: \(I = \dfrac{q}{t}\)
Ta có:
- Điện lượng: q = It = 4.2.60.60 = 28800 C
- Suất điện động của acquy nếu trong thời gian hoạt động trên đây nó sản sinh ra một công là 172,8 kJ là :
\(E = \dfrac{A}{q} = \dfrac{{172,{{8.10}^3}}}{{28800}} = 6V\)
Phát biểu nào sau đây là không đúng?
-
A.
Dòng điện có tác dụng từ. Ví dụ: nam châm điện.
-
B.
Dòng điện có tác dụng nhiệt. Ví dụ: bàn là điện.
-
C.
Dòng điện có tác dụng hoá học. Ví dụ: acquy nóng lên khi nạp điện.
-
D.
Dòng điện có tác dụng sinh lý. Ví dụ: hiện tượng điện giật.
Đáp án : C
A, B, D – đúng
C – sai vì : Dòng điện có tác dụng hóa học là đúng nhưng ví dụ về tác dụng hóa học là acquy nóng lên khi nạp điện là sai
Ví dụ về tác dụng hóa học của dòng điện : mạ đồng, mạ vàng, …
Cho đoạn mạch gồm điện trở \({R_1} = 100\Omega \), mắc nối tiếp với điện trở \({R_2} = 200\Omega \). Đặt vào hai đầu đoạn mạch một hiệu điện thế \(U\) khi đó hiệu điên thế giữa hai đầu điện trở \({R_1}\) là \(6{\rm{ }}\left( V \right)\). Hiệu điện thế giữa hai đầu đoạn mạch là:
-
A.
\(U{\rm{ }} = {\rm{ }}12{\rm{ }}\left( V \right)\)
-
B.
\(U{\rm{ }} = {\rm{ }}6{\rm{ }}\left( V \right)\)
-
C.
\(U{\rm{ }} = {\rm{ }}18{\rm{ }}\left( V \right)\)
-
D.
\(U{\rm{ }} = {\rm{ }}24{\rm{ }}\left( V \right)\)
Đáp án : C
+ Vận dụng biểu thức tính điện trở tương đương khi mắc nối tiếp: \({R_b} = {R_1} + {R_2} + ... + {R_n}\)
+ Vận dụng biểu thức định luật Ôm: \(I = \frac{U}{R}\)
+ Sử dụng biểu thức cường độ dòng điện trong đoạn mạch có các điện trở mắc nối tiếp: \(I = {I_1} = {I_2} = ... = {I_n}\)
+ Điện trở tương đương của mạch: \({R_b} = {R_1} + {R_2} = 100 + 200 = 300\Omega \)
+ Hiệu điện thế trên \({U_1} = 6V\)
Cường độ dòng điện \(I = {I_1} = \dfrac{{{U_1}}}{{{R_1}}} = \dfrac{6}{{100}} = 0,06A\)
+ Hiệu điện thế giữa hai đầu đoạn mạch: \(U = I.{R_b} = 0,06.300 = 18V\)
Biểu thức định luật Ôm cho toàn mạch trong trường hợp mạch ngoài chứa máy thu là:
-
A.
\(I = \frac{U}{R}\)
-
B.
\(I = \frac{E}{{R + r}}\)
-
C.
\(I = \frac{{E - {E_p}}}{{R + r + r'}}\)
-
D.
\(I = \frac{{{U_{AB}} + E}}{{{R_{AB}}}}\)
Đáp án : C
Biểu thức định luật Ôm cho toàn mạch trong trường hợp mạch ngoài có máy thu là: \(I = \frac{{E - {E_p}}}{{R + r + r'}}\)
Một pin có suất điện động 1,5V và điện trở trong là \(0,5\Omega \). Mắc một bóng đèn có điện trở \(2,5\Omega \) vào hai cực của pin này thành mạch điện kín. Cường độ dòng điện chạy qua đèn là
-
A.
2A
-
B.
1A
-
C.
1,5A
-
D.
0,5A
Đáp án : D
Áp dụng định luật Ohm cho toàn mạch \(I = \dfrac{\xi }{{r + R}}\)
Áp dụng định luật Ohm cho toàn mạch \(I = \dfrac{\xi }{{r + R}} = \dfrac{{1,5}}{{0,5 + 2,5}} = 0,5A\)
Để xác định điện trở trong r của một nguồn điện, một học sinh mắc mạch điện như hình (H1). Đóng khóa K và điều chỉnh con chạy C, kết quả đo được mô tả bởi đồ thị biểu diễn sự phụ thuộc của số chỉ U của vôn kế V vào số chỉ I của ampe kế A như hình (H2). Điện trở của vôn kế rất lớn. Biết \({R_0} = 2{\rm{0,3 \Omega }}\). Giá trị của r được xác định bởi thí nghiệm này là

-
A.
\({\rm{0,49 \Omega }}\)
-
B.
\({\rm{0,85 \Omega }}\)
-
C.
\({\rm{1,0 \Omega }}\)
-
D.
\({\rm{1,5 \Omega }}\)
Đáp án : A
Áp dụng công thức: \(U = \xi - I({R_0} + r)\)
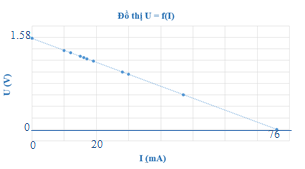
Từ đồ thị ta suy ra: \(1,58 = \xi \) và \(0 = 1,58 - ({{\rm{R}}_{\rm{0}}}{\rm{ + r)}}{\rm{.0,076}}\)
\( \Rightarrow {R_0} + r = 20,{\rm{79 (\Omega }}) \Rightarrow r = 0{\rm{,49 (\Omega )}}\)
Dấu hiệu tổng quát nhất để nhận biết dòng điện là:
-
A.
tác dụng hóa học.
-
B.
tác dụng từ.
-
C.
tác dụng nhiệt.
-
D.
tác dụng sinh lí.
Đáp án : B
Vận dụng lí thuyết về dòng điện
Ta có, tác dụng đặc trưng nhất của dòng điện là tác dụng từ.
Biểu thức nào sau đây là đúng
-
A.
\(q = \dfrac{I}{t}\)
-
B.
\(I = \dfrac{t}{q}\)
-
C.
\(q = {I^t}\)
-
D.
\(I = \dfrac{q}{t}\)
Đáp án : D
Cường độ dòng điện: \(I = \dfrac{q}{t}\)
Điện tích của electron là \( - {1,6.10^{ - 19}}C\), điện lượng chuyển qua tiết diện thẳng của dây dẫn trong \(30s\) là \(15C\). Số electron chuyển qua tiết diện thẳng của dây dẫn trong thời gian một giây là
-
A.
\({3,125.10^{18}}\)
-
B.
\({9,375.10^{19}}\)
-
C.
\({7,895.10^{19}}\)
-
D.
\({2,632.10^{18}}\)
Đáp án : A
+ Áp dụng biểu thức xác định cường độ dòng điện:\(I = \dfrac{{\Delta q}}{{\Delta t}}\)
+ Áp dụng biểu thức xác định số electron chuyển qua dây dẫn trong thời gian t: \(n = \dfrac{{I.t}}{{\left| e \right|}}.\)
Ta có:
+ Cường độ dòng điện trong mạch: \(I = \dfrac{{\Delta q}}{{\Delta t}} = \dfrac{{15}}{{30}} = 0,5A\)
+ Số electron chuyển qua tiết diện thẳng của dây dẫn trong thời gian một giây là: \(n = \dfrac{{I.t}}{{\left| e \right|}} = \dfrac{{0,5.1}}{{{{1,6.10}^{ - 19}}}} = {3,125.10^{18}}\)
Chọn phương án sai.
Khi một tải R nối vào nguồn suất điện động \(\xi \) và điện trở trong r, thấy công suất mạch ngoài cực đại thì:
-
A.
\(I = \dfrac{{{E}}}{{2R}}\)
-
B.
\(r = R\)
-
C.
\({P_R} = \dfrac{{{E^2}}}{{4r}}\)
-
D.
\(I = \dfrac{\xi }{r}\)
Đáp án : D
+ Vận dụng biểu thức tính công suất: \(P = {I^2}R\)
+ Vận dụng biểu thức định luật Ôm: \(I = \dfrac{E}{{R + r}}\)
+ Áp dụng bất đẳng thức cosi
Công suất mạch ngoài : \(P = {R_N}{I^2} = {\rm{ }}{R_N}.{\left( {\dfrac{E}{{{R_N} + r}}} \right)^2}\, = \,\dfrac{{{E^2}}}{{{{\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right)}^2}}}\)
Để \(P = {P_{Max}}\) thì \(\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right)\) nhỏ nhất.
Theo BĐT Cô-si thì : \(\left( {\sqrt {{R_N}} + \dfrac{r}{{\sqrt {{R_N}} }}} \right)\; \ge 2\sqrt r \)
Dấu “=” xảy ra khi \(\sqrt {{R_N}} \, = \,\dfrac{r}{{\sqrt {{R_N}} }}\,\, \Rightarrow \,{R_N}\, = \,r\)
Khi đó: \(P = {P_{{\rm{max}}}} = \dfrac{{{E^2}}}{{4r}}\)
=> Phương án D – sai vì: \(I = \dfrac{E}{{2r}} = \dfrac{E}{{2R}}\)
Cho mạch điện có sơ đồ như hình vẽ:

Biết, \(E = 6V,r = 1\Omega ,{R_1} = 4\Omega \), R là biến trở
Tìm R để công suất tiêu thụ trên R là cực đại? Tính giá trị công suất cực đại khi đó?
-
A.
\(R = \dfrac{3}{2}\Omega ,{P_{{\rm{max}}}} = 37,5{\rm{W}}\)
-
B.
\(R = \dfrac{2}{3}\Omega ,{P_{{\rm{max}}}} = 37,5{\rm{W}}\)
-
C.
\(R = \dfrac{4}{5}\Omega ,{P_{{\rm{max}}}} = 7,2{\rm{W}}\)
-
D.
\(R = \dfrac{5}{4}\Omega ,{P_{{\rm{max}}}} = 7,2{\rm{W}}\)
Đáp án : C
+ Vận dụng biểu thức tính công suất tiêu thụ trên R : \(P = {I^2}R = \dfrac{{{U^2}}}{R}\)
+ Vận dụng biểu thức tính cường độ dòng điện : \(I = \dfrac{E}{{R + r}}\)
+ Áp dụng bất đẳng thức cosi
Ta có: PR = \(\dfrac{{{U^2}}}{R}\)
Mặt khác: \({U_R} = {\rm{ }}I.{R_N} = \dfrac{E}{{\dfrac{{{R_1}.R}}{{{R_1} + R}} + r}}.\dfrac{{{R_1}.R}}{{{R_1} + R}}\, = \,\dfrac{{24R}}{{5R + 4}}\).
Vậy: \({P_R} = \dfrac{{{{24}^2}{R^2}}}{{{{\left( {5R + 4} \right)}^2}.R}}\, = \,\dfrac{{576}}{{{{\left( {5\sqrt R + \dfrac{4}{{\sqrt R }}} \right)}^2}}}\,\)
Theo BĐT Cô-si, ta có : \(\left( {5\sqrt R + \dfrac{4}{{\sqrt R }}} \right)\, \ge \,4\sqrt 5 \), dấu \('' = ''\) xảy ra khi : \(\left( {5\sqrt R = \dfrac{4}{{\sqrt R }}} \right)\) hay \(R = \dfrac{4}{5}\Omega \).
Vậy : \({P_{RMax}} = \dfrac{{576}}{{{{\left( {4\sqrt 5 } \right)}^2}}}\, = 7,2\,{\rm{W}}\) khi \(R = \dfrac{4}{5}\Omega \)
Một biến trở con chạy được làm bằng dây dẫn hợp kim Nikelin có điện trở suất \({4.10^{ - 7}}\Omega .m\), có tiết diện đầu là \(0,8m{m^2}\) và gồm \(300\) vòng cuốn quanh lõi sứ trụ tròn đường kính \(4,5cm\). Tính điện trở lớn nhất của biến trở này.
-
A.
\(21,2\Omega \)
-
B.
\(10\Omega \)
-
C.
\(15,3\Omega \)
-
D.
\(7,1\Omega \)
Đáp án : A
+ Sử dụng biểu thức tính chu vi vòng tròn: \(C = 2\pi R = \pi d\)
+ Sử dụng biểu thức tính điện trở: \(R = \rho \dfrac{l}{S}\)
Ta có:
+ Chiều dài của một vòng quấn là: \(C = 2\pi R = \pi d = 2\pi .0,045 = 0,1414m\)
+ Chiều dài của toàn bộ dây quấn: \(l = nC = 300.0,1414 = 42,42m\)
+ Điện trở \(R = \rho \dfrac{l}{S} = {4.10^{ - 7}}\dfrac{{42,42}}{{{{0,8.10}^{ - 6}}}} = 21,21\Omega \)
Đối với mạch điện kín, thì hiệu suất của nguồn điện không được tính bằng công thức:
-
A.
\(H = \dfrac{{{A_{coich}}}}{{{A_{nguon}}}}.100\% \)
-
B.
\(H = \dfrac{{{U_N}}}{E}.100\% \)
-
C.
\(H = \dfrac{{{R_N}}}{{{R_N} + r}}.100\% \)
-
D.
\(H = \dfrac{r}{{{R_N} + r}}.100\% \)
Đáp án : D
Vận dụng lí thuyết về hiệu suất của nguồn điện
Mạch ngoài thuần điện trở \({R_N}\) thì hiệu suất của nguồn điện có điện trở r được tính bởi biểu thức:
\(H = \dfrac{{{A_{coich}}}}{{{A_{nguon}}}}.100\% = \dfrac{{{U_N}}}{E}.100\% = \;\dfrac{{{R_N}}}{{{R_N} + r}}.100\% \)
=> Phương án D - sai
Cho 2 mạch điện như hình vẽ:

\({E_1} = 18V,{r_1} = 1\Omega \). Cho \(R = 9\Omega \), \({I_1} = 2,5A\), \({I_2} = 0,5A\). Tìm \({E_2}\) và \({r_2}\)
-
A.
\(\left\{ \begin{array}{l}{E_2} = 12V\\{r_2} = 1\Omega \end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}{E_2} = 12V\\{r_2} = 2\Omega \end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}{E_2} = 6V\\{r_2} = 1\Omega \end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}{E_2} = 6V\\{r_2} = 2\Omega \end{array} \right.\)
Đáp án : B
+ Xác định máy phát, máy thu
+ Sử dụng biểu thức định luật ôm cho toàn mạch: \(I = \dfrac{{{E_b}}}{{{R_N} + r}}\)
Từ mạch điện a, ta thấy 2 nguồn đều là máy phát, nên ta có:
Cường độ dòng điện cho mạch kín: \({I_1} = \dfrac{{{E_b}}}{{R + {r_b}}} = \dfrac{{{E_1} + {E_2}}}{{R + {r_1} + {r_2}}}\)
\( \Leftrightarrow 2,5 = \dfrac{{18 + {E_2}}}{{9 + 1 + {r_2}}}\)
\( \Rightarrow 2,5\left( {10 + {r_2}} \right) = 18 + {E_2}\)
\( \Rightarrow {E_2} - 2,5{r_2} = 7\) (1)
Từ mạch điện b, ta thấy máy 1 là máy phát còn máy 2 là máy thu, nên định luật ôm viết cho mạch kín chứa máy phát và máy thu là: \({I_2} = \dfrac{{{E_1} - {E_2}}}{{R + {r_1} + {r_2}}}\)
\( \Leftrightarrow 0,5 = \dfrac{{18 - {E_2}}}{{9 + 1 + {r_2}}}\)
\( \Rightarrow 0,5\left( {10 + {r_2}} \right) = 18 - {E_2}\)
\( \Rightarrow {E_2} + 0,5{r_2} = 13\) (2)
Từ (1) và (2), ta có: \(\left\{ \begin{array}{l}{E_2} - 2,5{r_2} = 7\\{E_2} + 0,5{r_2} = 13\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{E_2} = 12V\\{r_2} = 2\Omega \end{array} \right.\)
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận