Đề kiểm tra 15 phút chương 3: Dòng điện xoay chiều - Đề số 02

Làm đề thi

Đề bài

Câu 1 :

Cho đoạn mạch RLC nối tiếp có giá trị các phần tử cố định. Đặt vào hai đầu đoạn này một điện áp xoay chiều có tần số thay đổi. Khi tần số góc của dòng điện bằng ${\omega _0}$ thì cảm kháng và dung kháng có giá trị ${Z_L} = 10\Omega $ và${Z_C} = 90\Omega $. Để trong mạch xảy ra cộng hưởng, ta phải thay đổi tần số góc của dòng điện đến giá trị $\omega $ bằng:

A.

$3{\omega _0}$
B.

$2{\omega _0}$
C.

$\dfrac{{{\omega _0}}}{2}$
D.

$\dfrac{{{\omega _0}}}{3}$

Câu 2 :

Mạch điện nối tiếp gồm R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C thay đổi. Điện áp hai đầu ổn định là U, tần số f. Khi U_C cực đại, dung kháng Z_C có giá trị là:

A.

${Z_C} = \dfrac{{\sqrt {{R^2} + Z_L^2} }}{{{Z_L}}}$
B.

${Z_C} = R + {Z_L}$
C.

${Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}$
D.

${Z_C} = \dfrac{{{R^2} + Z_L^2}}{R}$

Câu 3 :

Trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Cho $L,{\rm{ }}R,\omega $ không đổi. Thay đổi C đến khi C=C₀ thì trong mạch xảy ra cộng hưởng. Phát biểu nào sau đây là sai?

A.

${Z_{\min }} = R$
B.

${I_{{\rm{max}}}} = \dfrac{U}{R}$
C.

${P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}$
D.

${\varphi _u} + {\varphi _i} = 0$

Câu 4 :

Đặt điện áp xoay chiều $u{\rm{ }} = {\rm{ }}{U_0}cos\omega t$có ${U_0}$ không đổi và tần số góc $\omega $ thay đổi được vào hai đầu đoạn mạch có $R,{\rm{ }}L,{\rm{ }}C$ mắc nối tiếp. Thay đổi $\omega $ thì tổng trở của mạch khi $\omega = {\omega _1}$ bằng tổng trở của mạch khi $\omega = {\omega _2}$. Hệ thức đúng là:

A.

${\omega _1} + {\omega _2} = \dfrac{2}{{LC}}$
B.

${\omega _1}{\omega _2} = \dfrac{1}{{\sqrt {LC} }}$
C.

${\omega _1} + {\omega _2} = \dfrac{2}{{\sqrt {LC} }}$
D.

${\omega _1}{\omega _2} = \dfrac{1}{{LC}}$

Câu 5 :

Cho đoạn mạch điện xoay chiều RLC có C thay đổi được. Khi $C = {C_1}$ và $C = {C_2}$ thì tổng trở của mạch không thay đổi. Khi đó ${Z_{{C_1}}} + {Z_{{C_2}}} = ?$

A.

${Z_{{C_1}}} + {Z_{{C_2}}} = {Z_L}$
B.

${Z_{{C_1}}} + {Z_{{C_2}}} = 2{Z_L}$
C.

${Z_{{C_1}}} + {Z_{{C_2}}} = \dfrac{{{Z_L}}}{2}$
D.

${Z_{{C_1}}} + {Z_{{C_2}}} = Z_L^2$

Câu 6 :

Trong mạch điện xoay chiều gồm $R,{\rm{ }}L,{\rm{ }}C$ mắc nối tiếp. Cho $C,{\rm{ }}R,\omega $ không đổi. Thay đổi L đến khi $L = {L_0}$ thì trong mạch xảy ra cộng hưởng. Phát biểu nào sau đây là đúng?

A.

${Z_{\min }} = 2R = 2\left| {{Z_L} - {Z_C}} \right|$
B.

${I_{{\rm{max}}}} = \dfrac{U}{{2R}}$
C.

${P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}$
D.

${\varphi _u} + {\varphi _i} = 0$

Câu 7 :

Đặt vào hai đầu một điện trở thuần một hiệu điện thế xoay chiều có giá trị cực đại U₀ công suất tiêu thụ trên R là P. Khi đặt vào hai đầu điện trở đó một hiệu điện thế không đổi có giá trị U₀ thì công suất tiêu thụ trên R là :

A.

P
B.

2P
C.

$\sqrt 2 $P
D.

4P

Câu 8 :

Trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Cho $C,{\rm{ }}R,\omega $ không đổi. Thay đổi L đến khi L=L₀ thì công suất P_max. Khi đó, P_max đó được xác định bởi biểu thức:

A.

${P_{{\rm{max}}}} = \dfrac{{{U^2}}}{R}$
B.

${P_{{\rm{max}}}} = \dfrac{{{U^2}}}{{2R}}$
C.

${P_{{\rm{max}}}} = I_0^2R$
D.

${P_{{\rm{max}}}} = \dfrac{{{U_0}^2}}{{{R^2}}}$

Câu 9 :

Một mạch điện xoay chiều gồm các linh kiện lý tưởng R, L, C mắc nối tiếp. Tần số góc riêng của mạch là w₀, điện trở R có thể thay đổi. Hỏi cần phải đặt vào mạch một điện áp xoay chiều có giá trị hiệu dụng không đổi, có tần số góc w bằng bao nhiêu để điện áp hiệu dụng U_RL không phụ thuộc vào R?

A.

$\omega = \frac{{{\omega _0}}}{{\sqrt 2 }}$
B.

$\omega = {\omega _0}$
C.

$\omega = {\omega _0}\sqrt 2 $
D.

$\omega = 2{\omega _0}$

Câu 10 :

Đặt điện áp $u = U\sqrt 2 {\rm{cos(}}\omega {\rm{t)V}}$ vào hai đầu đoạn mạch nối tiếp gồm $R = 100\Omega ,$ cuộn cảm có độ tự cảm L và tụ điện có điện dung C thay đổi được. Khi $C = {C_1} = \frac{{100}}{\pi }\mu F$ thì cường độ dòng điện qua mạch cực đại. Khi $C = \frac{{{C_1}}}{2}$thì điện áp ở đầu tụ điện đạt cực đại. Tần số góc ω bằng?

A.

200π rad/s
B.

125π rad/s
C.

100π rad/s
D.

120π rad/s

Câu 11 :

Đoạn mạch xoay chiều RLC. Cuộn thuần cảm có độ tự cảm thay đổi được, điện trở thuần $R{\rm{ }} = 100\Omega $.Hiệu điện thế hai đầu mạch $u = 200cos(100\pi t)V$. Khi thay đổi độ tự cảm của cuộn dây thì cường độ hiệu dung có giá trị cực đại là:

A.

$I = 2A$
B.

$I = 0,5A$
C.

$I = \dfrac{1}{{\sqrt 2 }}A$
D.

$I = \sqrt 2 A$

Câu 12 :

Đoạn mạch xoay chiều RLC nối tiếp , cuộn dây thuần cảm với $C{R^2} < 2L$; điện áp hai đầu đoạn mạch là $u = U\sqrt 2 cos\omega t$, U ổn định và $\omega $ thay đổi . Khi $\omega = {\omega _L}$ thì điện áp hai cuộn cảm L cực đại và ${U_{Lmax}} = \dfrac{{26U}}{{24}}$. Hệ số công suất tiêu thụ của cả đoạn mạch là :

A.

$\dfrac{1}{{\sqrt 5 }}$
B.

$\dfrac{{\sqrt 5 }}{3}$
C.

$\dfrac{{4\sqrt 5 }}{5}$
D.

$\dfrac{7}{{4\sqrt 5 }}$

Lời giải và đáp án

Câu 1 :

A.

$3{\omega _0}$
B.

$2{\omega _0}$
C.

$\dfrac{{{\omega _0}}}{2}$
D.

$\dfrac{{{\omega _0}}}{3}$

Đáp án : A

Phương pháp giải :

+ Sử dụng biểu thức tính cảm kháng ${Z_L} = \omega L$ và dung kháng ${Z_C} = \dfrac{1}{{\omega C}}$

+ Sử dụng công thức xác định tần số góc khi cộng hưởng: ${\omega ^2} = \dfrac{1}{{LC}}$

Lời giải chi tiết :

Ta có:

$\begin{array}{l}\left\{ \begin{array}{l}\dfrac{1}{{{\omega _0}C}} = 90\Omega \\{\omega _0}L = 10\Omega \end{array} \right.\\ \to \dfrac{{{Z_L}}}{{{Z_C}}} = \omega _0^2LC = \dfrac{{10}}{{90}} = \dfrac{1}{9}\\ \to \omega _0^2 = \dfrac{1}{{9LC}}\end{array}$

Khi mạch cộng hưởng: ${\omega ^2} = \dfrac{1}{{LC}} = 9\omega _0^2 \to \omega = 3{\omega _0}$

Câu 2 :

A.

${Z_C} = \dfrac{{\sqrt {{R^2} + Z_L^2} }}{{{Z_L}}}$
B.

${Z_C} = R + {Z_L}$
C.

${Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}$
D.

${Z_C} = \dfrac{{{R^2} + Z_L^2}}{R}$

Đáp án : C

Lời giải chi tiết :

C thay đổi để U_C max, khi đó: ${Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}$

Câu 3 :

A.

${Z_{\min }} = R$
B.

${I_{{\rm{max}}}} = \dfrac{U}{R}$
C.

${P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}$
D.

${\varphi _u} + {\varphi _i} = 0$

Đáp án : D

Lời giải chi tiết :

C thay đổi để mạch xảy ra cộng hưởng khi đó: ${Z_L} = {Z_C}$

A, B, C - đúng

D- sai vì khi đó u và i cùng pha với nhau

Câu 4 :

A.

${\omega _1} + {\omega _2} = \dfrac{2}{{LC}}$
B.

${\omega _1}{\omega _2} = \dfrac{1}{{\sqrt {LC} }}$
C.

${\omega _1} + {\omega _2} = \dfrac{2}{{\sqrt {LC} }}$
D.

${\omega _1}{\omega _2} = \dfrac{1}{{LC}}$

Đáp án : D

Lời giải chi tiết :

Theo đầu bài, ta có:

$\begin{array}{l}{Z_1} = {Z_2} \leftrightarrow Z_1^2 = Z_2^2\\ \leftrightarrow {R^2} + {\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)^2} = {R^2} + {\left( {{Z_{{L_2}}} - {Z_{{C_2}}}} \right)^2}\\ \to \left| {{Z_{{L_1}}} - {Z_{{C_1}}}} \right| = \left| {{Z_{{L_2}}} - {Z_{{C_2}}}} \right|\\ \to \left[ \begin{array}{l}{Z_{{L_1}}} + {Z_{{L_2}}} = {Z_{{C_1}}} + {Z_{{C_2}}}\\{Z_{{L_1}}} - {Z_{{C_1}}} = {Z_{{L_2}}} - {Z_{{C_2}}}(L)\end{array} \right.\end{array}$

Ta suy ra:

$\begin{array}{l}{Z_{{L_1}}} + {Z_{{L_2}}} = {Z_{{C_1}}} + {Z_{{C_2}}}\\ \leftrightarrow {\omega _1}L + {\omega _2}L = \dfrac{1}{{{\omega _1}C}} + \dfrac{1}{{{\omega _2}C}}\\ \leftrightarrow \left( {{\omega _1} + {\omega _2}} \right)L = \left( {\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}} \right)\dfrac{1}{C}\\ \leftrightarrow \left( {{\omega _1} + {\omega _2}} \right)L = \left( {\dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _1}{\omega _2}}}} \right)\dfrac{1}{C}\\ \to {\omega _1}{\omega _2} = \dfrac{1}{{LC}}\end{array}$

Câu 5 :

A.

${Z_{{C_1}}} + {Z_{{C_2}}} = {Z_L}$
B.

${Z_{{C_1}}} + {Z_{{C_2}}} = 2{Z_L}$
C.

${Z_{{C_1}}} + {Z_{{C_2}}} = \dfrac{{{Z_L}}}{2}$
D.

${Z_{{C_1}}} + {Z_{{C_2}}} = Z_L^2$

Đáp án : B

Lời giải chi tiết :

Khi ${Z_1} = {Z_2}$

${R^2} + {({Z_L} - {Z_{C1}})^2} = {R^2} + {({Z_L} - {Z_{C2}})^2} \to \left| {{Z_L} - {Z_{C1}}} \right| = \left| {{Z_L} - {Z_{C2}}} \right|$

Với ${Z_{C2}} > {Z_{C1}}$$ \to {Z_{C1}} + {Z_{C2}} = 2{Z_L}$

Câu 6 :

A.

${Z_{\min }} = 2R = 2\left| {{Z_L} - {Z_C}} \right|$
B.

${I_{{\rm{max}}}} = \dfrac{U}{{2R}}$
C.

${P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}$
D.

${\varphi _u} + {\varphi _i} = 0$

Đáp án : C

Lời giải chi tiết :

$L$ thay đổi để mạch xảy ra cộng hưởng khi đó: ${Z_L} = {Z_C}$ và $\left\{ \begin{array}{l}{Z_{\min }} = R\\{I_{{\rm{max}}}} = \dfrac{U}{R}\\{U_{{R_{max}}}} = U\\{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\end{array} \right.$

A – sai vì: ${Z_{\min }} = R$

B – sai vì: ${I_{max}} = \dfrac{U}{R}$

C - đúng

D - sai vì khi đó u và i cùng pha với nhau $\left( {{\varphi _u} = {\varphi _i}} \right)$

Câu 7 :

A.

P
B.

2P
C.

$\sqrt 2 $P
D.

4P

Đáp án : B

Phương pháp giải :

Vận dụng biểu thức tính công suất: $P = {I^2}R$

Lời giải chi tiết :

Khi đặt hiệu điện thế xoay chiều thì công suất tiêu thụ trên R là:

$P = {I^2}R = \dfrac{{U_0^2}}{{2R}}$

Khi đặt hiệu điện thế không đổi thì công suất tiêu thụ trên R là :

$P' = \dfrac{{U_0^2}}{R}$

$ \Rightarrow P' = 2P$

Câu 8 :

A.

${P_{{\rm{max}}}} = \dfrac{{{U^2}}}{R}$
B.

${P_{{\rm{max}}}} = \dfrac{{{U^2}}}{{2R}}$
C.

${P_{{\rm{max}}}} = I_0^2R$
D.

${P_{{\rm{max}}}} = \dfrac{{{U_0}^2}}{{{R^2}}}$

Đáp án : A

Lời giải chi tiết :

Thay đổi L đến khi L=L₀ thì điện áp P_max khi đó, xảy ra cộng hưởng điện :${Z_L} = {Z_C}$

Công suất đạt giá trị cực đại: ${P_{{\rm{max}}}} = \dfrac{{{U^2}}}{R}$

Câu 9 :

A.

$\omega = \frac{{{\omega _0}}}{{\sqrt 2 }}$
B.

$\omega = {\omega _0}$
C.

$\omega = {\omega _0}\sqrt 2 $
D.

$\omega = 2{\omega _0}$

Đáp án : A

Phương pháp giải :

+ Sử dụng công thức tính tần số góc

+ Sử dụng công thức tính hiệu điện thế: U=IZ => Viết biểu thức U_RL

Lời giải chi tiết :

Ta có :

${\omega _0} = \frac{1}{{\sqrt {LC} }}$

${U_{RL}} = {\rm{ }}I.{Z_{RL\;}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \frac{U}{{\sqrt {1 + \frac{{{Z_C}^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}}} }}$

U_RLkhông phụ thuộc vào R

$ \leftrightarrow {Z_C} = 2{Z_L}\; \to \omega = \frac{1}{{\sqrt {2LC} }} = \frac{{{\omega _0}}}{{\sqrt 2 }}$

Câu 10 :

A.

200π rad/s
B.

125π rad/s
C.

100π rad/s
D.

120π rad/s

Đáp án : C

Lời giải chi tiết :

Ta có:

+ Khi C = C₁: cường độ dòng điện qua mạch cực đại

=> Khi đó mạch cộng hưởng: ${Z_{{C_1}}} = {Z_L}$ (1)

+ Khi $C = \frac{{{C_1}}}{2} \to {Z_C} = 2{Z_{{C_1}}}$: thì U_C max, khi đó ta có:

${Z_C} = \frac{{{R^2} + Z_L^2}}{{{Z_L}}} = 2{Z_{{C_1}}}$ (2)

Từ (1) và (2): $ \to \frac{{{R^2} + {Z_L}^2}}{{{Z_L}}} = 2{Z_L} \to R = {Z_L} = {Z_{{C_1}}} = 100\Omega $

Mặt khác: ${Z_{{C_1}}} = \frac{1}{{\omega {C_1}}} \to \omega = \frac{1}{{{Z_{{C_1}}}.{C_1}}} = \frac{1}{{100.\frac{{100}}{\pi }{{.10}^{ - 6}}}} = 100\pi (ra{\rm{d}}/s)$

Câu 11 :

A.

$I = 2A$
B.

$I = 0,5A$
C.

$I = \dfrac{1}{{\sqrt 2 }}A$
D.

$I = \sqrt 2 A$

Đáp án : D

Lời giải chi tiết :

L thay đổi để I_max, khi đó: ${I_{{\rm{max}}}} = \dfrac{U}{R} = \dfrac{{\dfrac{{200}}{{\sqrt 2 }}}}{{100}} = \sqrt 2 (A)$

Câu 12 :

A.

$\dfrac{1}{{\sqrt 5 }}$
B.

$\dfrac{{\sqrt 5 }}{3}$
C.

$\dfrac{{4\sqrt 5 }}{5}$
D.

$\dfrac{7}{{4\sqrt 5 }}$

Đáp án : B

Phương pháp giải :

+ Sử dụng giản đồ véc-tơ

+ $\omega $ thay đổi để ${U_{{L_{max}}}}$ khi đó: $Z_L^2 = {Z^2} + Z_C^2$ và $\dfrac{{{R^2}}}{2} = {Z_C}\left( {{Z_L} - {Z_C}} \right)$

+ Sử dụng biểu thức tính hệ số công suất: $cos\varphi = \dfrac{R}{Z}$

Lời giải chi tiết :

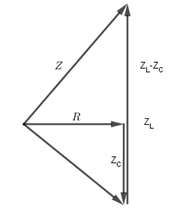
Ta có: ${U_{{L_{max}}}} = I.{Z_L} = \dfrac{U}{Z}.{Z_L}$

Theo đầu bài, ta có: ${U_{Lmax}} = \dfrac{{26}}{{24}}U$

Ta có thể giả sử: $Z = 24\Omega ;{Z_L} = 26\Omega $

Khi đó:

$\begin{array}{l}Z_L^2 = {Z^2} + Z_C^2\\ \Rightarrow {Z_C} = \sqrt {Z_L^2 - {Z^2}} = \sqrt {{{26}^2} - {{24}^2}} = 10\Omega \end{array}$

Lại có:

$\begin{array}{l}\dfrac{{{R^2}}}{2} = {Z_C}\left( {{Z_L} - {Z_C}} \right)\\ \Rightarrow R = \sqrt {2{Z_C}\left( {{Z_L} - {Z_C}} \right)} = \sqrt {2.10\left( {26 - 10} \right)} = 8\sqrt 5 \Omega \end{array}$

Hệ số công suất của mạch khi đó: $cos\varphi = \dfrac{R}{Z} = \dfrac{{8\sqrt 5 }}{{24}} = \dfrac{{\sqrt 5 }}{3}$

Đề kiểm tra 15 phút chương 3: Dòng điện xoay chiều - Đề số 03

Xem chi tiết

Đề kiểm tra 15 phút chương 4: Dao động và sóng điện từ - Đề số 1

Xem chi tiết

Đề kiểm tra 15 phút chương 4: Dao động và sóng điện từ - Đề số 2

Xem chi tiết

Đề kiểm tra 15 phút chương 4: Dao động và sóng điện từ - Đề số 3

Xem chi tiết

Đề kiểm tra 15 phút chương 5: Sóng ánh sáng - Đề số 1

Xem chi tiết

Đề kiểm tra 15 phút chương 5: Sóng ánh sáng - Đề số 2

Xem chi tiết

Đề kiểm tra 15 phút chương 5: Sóng ánh sáng - Đề số 3

Xem chi tiết

Đề kiểm tra 15 phút chương 6: Lượng tử ánh sáng - Đề số 1

Xem chi tiết

Đề kiểm tra 15 phút chương 6: Lượng tử ánh sáng - Đề số 2

Xem chi tiết

Đề kiểm tra 15 phút chương 6: Lượng tử ánh sáng - Đề số 3

Xem chi tiết

Đề kiểm tra 15 phút chương 7: Hạt nhân nguyên tử - Đề số 1

Xem chi tiết

Đề kiểm tra 15 phút chương 7: Hạt nhân nguyên tử - Đề số 2

Xem chi tiết

Đề kiểm tra 15 phút chương 7: Hạt nhân nguyên tử - Đề số 3

Xem chi tiết

Đề kiểm tra 15 phút chương 3: Dòng điện xoay chiều - Đề số 01

Xem chi tiết

Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - Đề số 03

Xem chi tiết

Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - Đề số 02

Xem chi tiết

Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - Đề số 01

Xem chi tiết

Đề kiểm tra 15 phút chương 1: Dao động cơ - Đề số 04

Xem chi tiết

Đề kiểm tra 15 phút chương 1: Dao động cơ - Đề số 03

Xem chi tiết

Đề kiểm tra 15 phút chương 1: Dao động cơ - Đề số 02

Xem chi tiết

Đề kiểm tra 15 phút chương 1: Dao động cơ - Đề số 01

Xem chi tiết

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục

Bài giải mới nhất

Đề kiểm tra 15 phút chương 3: Dòng điện xoay chiều - Đề số 02

Báo lỗi góp ý