Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - Đề số 01
Đề bài
Một người ngồi ở bờ biển quan sát thấy khoảng cách giữa năm ngọn sóng liên tiếp bằng $20 m$. Bước sóng là:
-
A.
$5 m$
-
B.
$4 m$
-
C.
$16 m$
-
D.
$40 m$
Sóng ngang là:
-
A.
Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
-
B.
Sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
-
C.
Sóng trong đó các phần tử của môi trường dao động theo phương song song với phương truyền sóng
-
D.
Sóng trong đó các phần tử của môi trường dao động theo cả hai phương vuông góc và song song với phương truyền
Một người ngồi ở bờ biển đếm được $20$ ngọn sóng đi qua trước mặt trong $76s$. Chu kì dao động của nước biển là:
-
A.
$2s$
-
B.
$3,6s$
-
C.
$3,8s$
-
D.
$4s$
Một sóng cơ học có bước sóng $λ$ truyền theo một đường thẳng từ điểm $M$ đến điểm $N$. Biết khoảng cách $MN = d$. Độ lệch pha $\Delta \varphi $ của dao động tại hai điểm $M$ và $N$ là:
-
A.
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
-
B.
\(\Delta \varphi = \dfrac{{\pi d}}{\lambda }\)
-
C.
\(\Delta \varphi = \dfrac{{\pi \lambda }}{d}\)
-
D.
\(\Delta \varphi = \dfrac{{2\pi \lambda }}{d}\)
Bước sóng là:
-
A.
Quãng đường mà mỗi phần tử của môi trường đi được trong 1s
-
B.
Khoảng cách giữa hai phần tử của sóng dao động ngược pha.
-
C.
Khoảng cách giữa hai phần tử sóng gần nhất trên phương truyền sóng dao động cùng pha.
-
D.
Khoảng cách giữa hai vị trí xa nhau nhất của mỗi phần tử của sóng
Một dây đàn hồi dài có đầu $A$ dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng trên dây là $4m/s$. Xét một điểm $M$ trên dây và cách $A$ một đoạn $40cm$, người ta thấy $M$ luôn luôn dao động lệch pha so với $A$ một góc \(\Delta \varphi = (k + 0,5)\pi \) với $k$ là số nguyên. Tính tần số, biết tần số $f$ có giá trị trong khoảng từ $8 Hz$ đến $13 Hz$.
-
A.
$8,5Hz$
-
B.
$10Hz$
-
C.
$12Hz$
-
D.
$12,5Hz$
Sóng truyền theo phương ngang trên một sợi dây dài với tần số \(15Hz\). Điểm M trên dây tại một thời điểm đang ở vị trí cao nhất và tại thời điểm đó điểm N cách M \(5cm\) đang đi qua vị trí có li độ bằng nửa biên độ và đi lên. Coi biên độ sóng không đổi khi truyền. Biết khoảng cách MN nhỏ hơn bước sóng của sóng trên dây. Chọn đáp án đúng cho tốc độ truyền sóng và chiều truyền sóng.
-
A.
90 cm/s, truyền từ M đến N
-
B.
9 m/s, truyền từ M đến N
-
C.
4,5 m/s, truyền từ N đến M
-
D.
90cm/s, từ truyền N đến M
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình sóng tại nguồn O là: \({u_O} = A\sin \left( {\dfrac{{2\pi }}{T}t + \dfrac{\pi }{3}} \right)(cm)\) Một điểm M cách nguồn O bằng \(\dfrac{1}{3}\) bước sóng ở thời điểm \(t = \dfrac{T}{2}\) có ly độ \({u_M} = 3(cm)\) Biên độ sóng A là:
-
A.
\(\dfrac{4}{{\sqrt 3 }}\left( {cm} \right)\)
-
B.
\(2\sqrt 3 (cm)\)
-
C.
\(6\left( {cm} \right)\)
-
D.
\(1,5cm\)
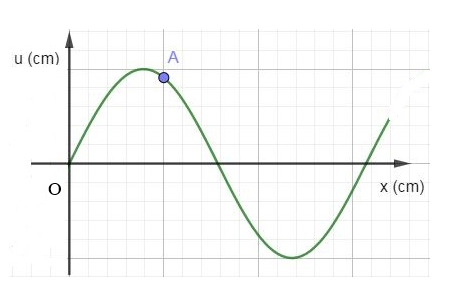
Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox. Tại thời điểm \({t_0}\) một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử A và O dao động lệch pha nhau?
-
A.
\(\dfrac{{5\pi }}{4}ra{\rm{d}}\)
-
B.
\(\dfrac{{3\pi }}{4}ra{\rm{d}}\)
-
C.
\(\dfrac{{3\pi }}{8}ra{\rm{d}}\)
-
D.
\(\dfrac{{5\pi }}{8}ra{\rm{d}}\)
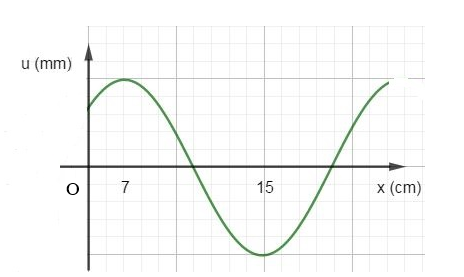
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng:
-
A.
8 cm
-
B.
16 cm
-
C.
32 cm
-
D.
64 cm
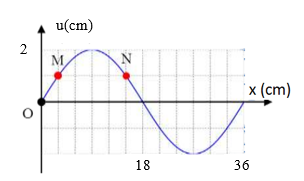
Một sóng ngang hình sin truyền trên một sợi dây dài. Hình vẽ bên là hình dạng của một đoạn dây tại một thời điểm xác định. Trong quá trình lan truyền sóng, khoảng cách lớn nhất giữa hai phần tử M và N có giá trị gần nhất với giá trị nào sau đây?
-
A.
12,12 cm
-
B.
18,3 cm
-
C.
12,5 cm
-
D.
8,72 cm
Sóng dọc không truyền được trong
-
A.
chân không.
-
B.
kim loại.
-
C.
không khí.
-
D.
nước.
Lời giải và đáp án
Một người ngồi ở bờ biển quan sát thấy khoảng cách giữa năm ngọn sóng liên tiếp bằng $20 m$. Bước sóng là:
-
A.
$5 m$
-
B.
$4 m$
-
C.
$16 m$
-
D.
$40 m$
Đáp án : A
Khoảng cách giữa $n$ ngọn sóng liên tiếp là: $n - 1$ bước sóng
Ta có, khoảng cách giữa năm ngọn sóng liên tiếp là: $4λ = 20 m => λ = 5m$
Sóng ngang là:
-
A.
Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
-
B.
Sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
-
C.
Sóng trong đó các phần tử của môi trường dao động theo phương song song với phương truyền sóng
-
D.
Sóng trong đó các phần tử của môi trường dao động theo cả hai phương vuông góc và song song với phương truyền
Đáp án : A
Sóng ngang: là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
Một người ngồi ở bờ biển đếm được $20$ ngọn sóng đi qua trước mặt trong $76s$. Chu kì dao động của nước biển là:
-
A.
$2s$
-
B.
$3,6s$
-
C.
$3,8s$
-
D.
$4s$
Đáp án : D
Thời gian truyền giữa n ngọn sóng liên tiếp là: $n - 1$ chu kì
Ta có, $20$ ngọn sóng đi qua trước mặt tương đương với $19$ bước sóng hay $19$ chu kì dao động
=> $19T = 76s => T = 4s$
Một sóng cơ học có bước sóng $λ$ truyền theo một đường thẳng từ điểm $M$ đến điểm $N$. Biết khoảng cách $MN = d$. Độ lệch pha $\Delta \varphi $ của dao động tại hai điểm $M$ và $N$ là:
-
A.
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
-
B.
\(\Delta \varphi = \dfrac{{\pi d}}{\lambda }\)
-
C.
\(\Delta \varphi = \dfrac{{\pi \lambda }}{d}\)
-
D.
\(\Delta \varphi = \dfrac{{2\pi \lambda }}{d}\)
Đáp án : A
Độ lệch pha của hai dao động tại hai điểm M và N là: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Bước sóng là:
-
A.
Quãng đường mà mỗi phần tử của môi trường đi được trong 1s
-
B.
Khoảng cách giữa hai phần tử của sóng dao động ngược pha.
-
C.
Khoảng cách giữa hai phần tử sóng gần nhất trên phương truyền sóng dao động cùng pha.
-
D.
Khoảng cách giữa hai vị trí xa nhau nhất của mỗi phần tử của sóng
Đáp án : C
Bước sóng $\lambda $: là quãng đường mà sóng truyền được trong một chu kỳ.
(Bước sóng $\lambda $ cũng là khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng dao động cùng pha).
Một dây đàn hồi dài có đầu $A$ dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng trên dây là $4m/s$. Xét một điểm $M$ trên dây và cách $A$ một đoạn $40cm$, người ta thấy $M$ luôn luôn dao động lệch pha so với $A$ một góc \(\Delta \varphi = (k + 0,5)\pi \) với $k$ là số nguyên. Tính tần số, biết tần số $f$ có giá trị trong khoảng từ $8 Hz$ đến $13 Hz$.
-
A.
$8,5Hz$
-
B.
$10Hz$
-
C.
$12Hz$
-
D.
$12,5Hz$
Đáp án : D
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Áp dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Độ lệch pha giữa $M$ và $A$:
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi d}}{{\dfrac{v}{f}}} \\\Rightarrow \dfrac{{2\pi df}}{v} = (k + 0,5)\pi \\\Rightarrow f = \left( {k + 0,5} \right)\dfrac{v}{{2d}} = 5\left( {k + 0,5} \right)Hz\)
Theo đầu bài:
\(8Hz < f < 13Hz \\\Rightarrow 8 < \left( {k + 0,5} \right).5 <13\\\Rightarrow 1,1 < k < 2,1 \\\Rightarrow k = 2 \\\Rightarrow f = 12,5Hz\)
Sóng truyền theo phương ngang trên một sợi dây dài với tần số \(15Hz\). Điểm M trên dây tại một thời điểm đang ở vị trí cao nhất và tại thời điểm đó điểm N cách M \(5cm\) đang đi qua vị trí có li độ bằng nửa biên độ và đi lên. Coi biên độ sóng không đổi khi truyền. Biết khoảng cách MN nhỏ hơn bước sóng của sóng trên dây. Chọn đáp án đúng cho tốc độ truyền sóng và chiều truyền sóng.
-
A.
90 cm/s, truyền từ M đến N
-
B.
9 m/s, truyền từ M đến N
-
C.
4,5 m/s, truyền từ N đến M
-
D.
90cm/s, từ truyền N đến M
Đáp án : D
+ Sử dụng vòng tròn lượng giác.
+ Vận dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }\)
+ Áp dụng công thức tính tốc độ truyền sóng: \(v = \lambda f\)
Ta có:
+ Điểm M ở vị trí cao nhất tức là biên dương.
+ Điểm N qua vị trí có li độ bằng \(\dfrac{A}{2}\) và đang đi lên
Vẽ trên vòng tròn lượng giác, ta được:
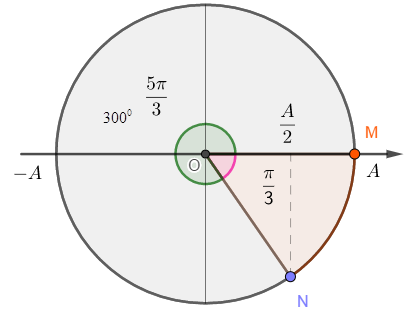
Ta có 2 trường hợp của góc lệch pha giữa M và N:
+ TH 1: M, N lệch pha nhau: \(\Delta \varphi = \dfrac{\pi }{3}\)
\(\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{\pi }{3}\\ \to \lambda = 6\Delta d = 6.5 = 30cm\\ \to v = \lambda f = 30.15 = 450cm/s = 4,5m/s\end{array}\)
M sớm pha hơn N => Sóng truyền từ M đến N
+ TH 2: M, N lệch pha nhau \(\Delta \varphi = \dfrac{{5\pi }}{3}\)
\(\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{5\pi }}{3}\\ \to \lambda = \dfrac{6}{5}\Delta d = \dfrac{6}{5}.5 = 6cm\\ \to v = \lambda f = 6.15 = 90cm/s\end{array}\)
Do N sớm pha hơn M
=> Sóng truyền từ N đến M
Một sóng cơ học lan truyền dọc theo một đường thẳng có phương trình sóng tại nguồn O là: \({u_O} = A\sin \left( {\dfrac{{2\pi }}{T}t + \dfrac{\pi }{3}} \right)(cm)\) Một điểm M cách nguồn O bằng \(\dfrac{1}{3}\) bước sóng ở thời điểm \(t = \dfrac{T}{2}\) có ly độ \({u_M} = 3(cm)\) Biên độ sóng A là:
-
A.
\(\dfrac{4}{{\sqrt 3 }}\left( {cm} \right)\)
-
B.
\(2\sqrt 3 (cm)\)
-
C.
\(6\left( {cm} \right)\)
-
D.
\(1,5cm\)
Đáp án : B
Áp dụng biểu thức xác định độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }\)
+ Viết phương trình sóng tại M
+ Thay x và t vào phương trình sóng
+ Ta có:
\(\begin{array}{l}{u_O} = A\sin \left( {\dfrac{{2\pi }}{T}t + \dfrac{\pi }{3}} \right)(cm)\\ \to {u_M}{\rm{ = Asin}}\left( {\dfrac{{2\pi }}{T}t + \dfrac{\pi }{3} - \dfrac{{2\pi x}}{\lambda }} \right)cm\end{array}\)
+ Thay \(t = \dfrac{T}{2}\) và \(x = \dfrac{\lambda }{3}\) vào phương trình dao động tại M, ta được:
\(\begin{array}{l}{u_M}{\rm{ = Asin}}\left( {\dfrac{{2\pi }}{T}t + \dfrac{\pi }{3} - \dfrac{{2\pi x}}{\lambda }} \right)\\ \leftrightarrow {\rm{Asin}}\left( {\dfrac{{2\pi }}{T}\dfrac{T}{2} + \dfrac{\pi }{3} - \dfrac{{2\pi \dfrac{\lambda }{3}}}{\lambda }} \right) = 3\\ \to A\sin \left( {\dfrac{{2\pi }}{3}} \right) = 3\\ \to A = 2\sqrt 3 cm\end{array}\)
Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox. Tại thời điểm \({t_0}\) một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử A và O dao động lệch pha nhau?

-
A.
\(\dfrac{{5\pi }}{4}ra{\rm{d}}\)
-
B.
\(\dfrac{{3\pi }}{4}ra{\rm{d}}\)
-
C.
\(\dfrac{{3\pi }}{8}ra{\rm{d}}\)
-
D.
\(\dfrac{{5\pi }}{8}ra{\rm{d}}\)
Đáp án : D
+ Sử dụng phương pháp đọc đồ thị dao động sóng
+ Áp dụng biểu thức tính độ lệch pha giữa 2 điểm: \(\Delta \varphi = \dfrac{{2\pi \Delta x}}{\lambda }\)
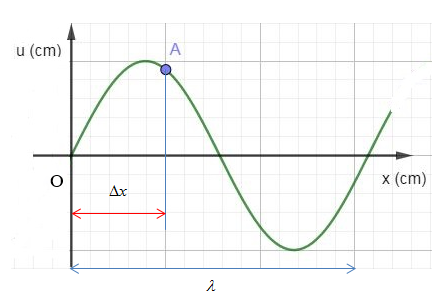
Từ đồ thị ta có:
\(\Delta x = \) 5 ô
\(\lambda = \) 16 ô
\( \to \dfrac{{\Delta x}}{\lambda } = \dfrac{5}{{16}}\)
=> Độ lệch pha giữa 2 điểm O và M là: \(\Delta \varphi = \dfrac{{2\pi \Delta x}}{\lambda } = 2\pi \dfrac{5}{{16}} = \dfrac{{5\pi }}{8}{\rm{r}}a{\rm{d}}\)
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng:

-
A.
8 cm
-
B.
16 cm
-
C.
32 cm
-
D.
64 cm
Đáp án : B
+ Sử dụng phương pháp đọc đồ thị dao động sóng
+ Khoảng cách giữa hai bụng sóng: \(\frac{\lambda }{2}\)
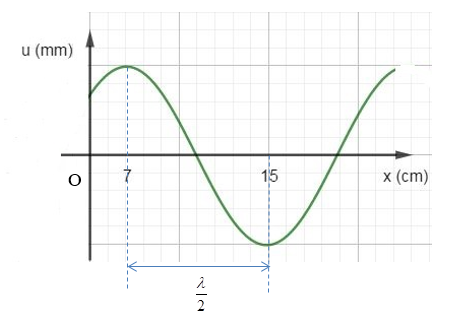
Từ đồ thị ta có: \(\frac{\lambda }{2} = 15 - 7 = 8 \to \lambda = 16cm\)
Một sóng ngang hình sin truyền trên một sợi dây dài. Hình vẽ bên là hình dạng của một đoạn dây tại một thời điểm xác định. Trong quá trình lan truyền sóng, khoảng cách lớn nhất giữa hai phần tử M và N có giá trị gần nhất với giá trị nào sau đây?

-
A.
12,12 cm
-
B.
18,3 cm
-
C.
12,5 cm
-
D.
8,72 cm
Đáp án : C
+ Sử dụng phương pháp đọc đồ thị dao động sóng
+ Áp dụng biểu thức tính độ lệch pha giữa 2 phần tử: \(\Delta \varphi = \frac{{2\pi \Delta x}}{\lambda }\)
+ Áp dụng công thức tính khoảng cách giữa hai phần tử sóng: \(d = \sqrt {\Delta {x^2} + \Delta {u^2}} \)
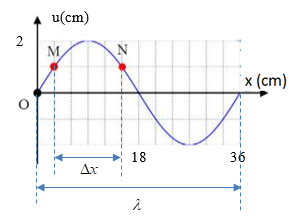
Từ đồ thị, ta có: \(\lambda = 36cm\), \(\Delta x = 12cm\)
Độ lệch pha giữa 2 phần tử: \(\Delta \varphi = \frac{{2\pi \Delta x}}{\lambda } = \frac{{2\pi .12}}{{36}} = \frac{{2\pi }}{3}ra{\rm{d}}\)
Khoảng cách giữa hai phần tử sóng: \(d = \sqrt {\Delta {x^2} + \Delta {u^2}} \)
với \(\Delta x\) là không đổi, \(d\) lớn nhất khi \(\Delta u\) lớn nhất
Ta có:
\(\begin{array}{l}\Delta u = {\left( {{u_M} - {u_N}} \right)_{{\rm{max}}}}\\ = \sqrt {{A^2} + {A^2} - 2{\rm{AAcos}}\left( {\Delta \varphi } \right)} \\ = \sqrt {{A^2} + {A^2} - 2{\rm{AAcos}}\left( {\frac{{2\pi }}{3}} \right)} \\ = \sqrt 3 A = 2\sqrt 3 cm\end{array}\)
\( \to {d_{{\rm{max}}}} = \sqrt {\Delta {x^2} + \Delta {u_{{\rm{max}}}}^2} = \sqrt {{{12}^2} + {{\left( {2\sqrt 3 } \right)}^2}} \approx 12,5cm\)
Sóng dọc không truyền được trong
-
A.
chân không.
-
B.
kim loại.
-
C.
không khí.
-
D.
nước.
Đáp án : A
Sóng dọc không truyền được trong chân không.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận