Đề kiểm tra 1 tiết chương 2: Sóng cơ và sóng âm - Đề số 01
Đề bài
Một sóng cơ dao động có bước sóng là $λ$. Khoảng cách giữa $n$ ngọn sóng liên tiếp là:
-
A.
$n$ bước sóng
-
B.
$n - 1$ bước sóng
-
C.
$n + 1$ bước sóng
-
D.
$2n$ bước sóng
Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục $Ox$. Tại thời điểm $t_0$ một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử $M$ và $O$ dao động lệch pha nhau?
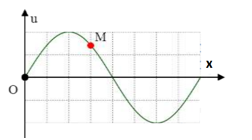
-
A.
\(\dfrac{\pi }{4}ra{\rm{d}}\)
-
B.
\(\dfrac{\pi }{3}ra{\rm{d}}\)
-
C.
\(\dfrac{{3\pi }}{4}ra{\rm{d}}\)
-
D.
\(\dfrac{{2\pi }}{3}ra{\rm{d}}\)
Nhận xét nào sau đây là sai khi nói về sóng âm
-
A.
Sóng âm là sóng cơ học truyền được trong cả 3 môi trường rắn, lỏng, khí
-
B.
Trong cả 3 môi trường rắn, lỏng, khí sóng âm luôn là sóng dọc
-
C.
Trong chất rắn sóng âm có cả sóng dọc và sóng ngang
-
D.
Âm thanh có tần số từ 16 Hz đến 20 kHz
Sóng ngang là:
-
A.
Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
-
B.
Sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
-
C.
Sóng trong đó các phần tử của môi trường dao động theo phương song song với phương truyền sóng
-
D.
Sóng trong đó các phần tử của môi trường dao động theo cả hai phương vuông góc và song song với phương truyền
Khi có sóng dừng trên dây, khoảng cách giữa hai nút liên tiếp bằng
-
A.
Một số nguyên lần bước sóng.
-
B.
Một phần tư bước sóng.
-
C.
Một nửa bước sóng.
-
D.
Một bước sóng.
Mối liên hệ giữa bước sóng $λ$, vận tốc truyền sóng $v$, chu kì $T$ và tần số $f$ của một sóng là:
-
A.
\(f = \dfrac{1}{T} = \dfrac{v}{\lambda }\)
-
B.
\(v = \dfrac{1}{f} = \dfrac{T}{\lambda }\)
-
C.
\(\lambda = \dfrac{T}{v} = \dfrac{f}{v}\)
-
D.
\(\lambda = \dfrac{T}{v} = vf\)
Dùng một âm thoa có tần số rung f = 100Hz người ta tạo ra hai điểm S1,S2 trên mặt nước hai nguồn sóng cùng biên độ,cùng pha.S1S2 = 3,2cm.Tốc độ truyền sóng là 40 cm/s. I là trung điểm của S1S2. Định những điểm dao động cùng pha với I.Tính khoảng từ I đến điểm M gần I nhất dao động cùng pha với I và nằm trên trung trực S1S2 là:
-
A.
1,81cm
-
B.
1,31cm
-
C.
1,20cm
-
D.
1,26cm
Sóng dừng xảy ra trên dây đàn hồi cố định có 1 bụng sóng khi:
-
A.
Chiều dài của dây bằng một phần tư bước sóng.
-
B.
Chiều dài bước sóng gấp đôi chiều dài của dây.
-
C.
Chiều dài của dây bằng bước sóng.
-
D.
Chiều dài bước sóng bằng một số lẻ chiều dài của dây.
Một sóng cơ truyền trên trục Ox trên một dây đàn hồi rất dài với tần số f = 1/3 Hz. Tại thời điểm t0 = 0 và tại thời điểm t1 = 0,875s hình ảnh của sợi dây được mô tả như hình vẽ. Biết rằng: d2 - d1 = 10 cm. Gọi δ là tỉ số giữa tốc độ dao động cực đại của phần tử trên dây và tốc độ truyền sóng. Giá trị của δ là:
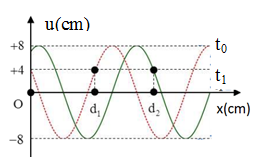
-
A.
π
-
B.
\(\dfrac{{3\pi }}{5}\)
-
C.
\(\dfrac{{5\pi }}{3}\)
-
D.
2π
Tại hai điểm A, B trong môi trường truyền sóng có hai nguồn kết hợp dao động cùng phương với phương trình lần lượt là : ${u_A} = a.cos(\omega t)(cm)$ và ${u_B} = a.cos(\omega t + \pi )(cm)$. Biết vận tốc và biên độ do mỗi nguồn truyền đi không đổi trong quá trình truyền sóng. Trong khoảng giữa Avà B có giao thoa sóng do hai nguồn trên gây ra. Phần tử vật chất tại trung điểm O của đoạn AB dao động với biên độ bằng :
-
A.
a/2
-
B.
2a
-
C.
0
-
D.
a
Một sợi dây $AB$ dài $100 cm$ căng ngang, đầu $B$ cố định, đầu $A$ gắn với một nhánh của âm thoa dao động điều hòa với tần số $40 Hz$. Trên dây $AB$ có một sóng dừng ổn định, $A$ được coi là nút sóng. Tốc độ truyền sóng trên dây là $20 m/s$. Tìm số nút sóng và bụng sóng trên dây, kể cả $A$ và $B$.
-
A.
$3$ bụng và $4$ nút
-
B.
$4$ bụng và $4$ nút
-
C.
$4$ bụng và $5$ nút
-
D.
$5$ bụng và $5$ nút
Một sợi dây đàn hồi nằm ngang có điểm đầu O dao động theo phương thẳng đứng với biên độ A = 5cm, T = 0,5s. Vận tốc truyền sóng là 40cm/s. Viết phương trình sóng tại M cách O d = 50 cm.
-
A.
\({u_M} = 5\cos (4\pi t - 5\pi )(cm)\)
-
B.
\({u_M} = 5\cos (4\pi t - 2,5\pi )(cm)\)
-
C.
\({u_M} = 5\cos (4\pi t + \pi )(cm)\)
-
D.
\({u_M} = 5\cos (4\pi t - 25\pi )(cm)\)
Một dây đàn dài $15cm$, khi gảy phát ra âm cơ bản với tốc độ truyền sóng trên dây là $300m/s$. Tốc độ truyền âm trong không khí là $340m/s$. Bước sóng của âm phát ra trong không khí là:
-
A.
$0,5m$
-
B.
$1,24m$
-
C.
$0,34m$
-
D.
$0,68m$
Giao thoa sóng nước với hai nguồn giống hệt nhau A, B cách nhau 20cm có tần số 50Hz. Tốc độ truyền sóng trên mặt nước là 1,5m/s. Trên mặt nước xét đường tròn tâm A, bán kính AB. Điểm trên đường tròn dao động với biên độ cực đại cách đường thẳng qua A, B một đoạn gần nhất là:
-
A.
18,67mm
-
B.
17,96mm
-
C.
19,97mm
-
D.
15,34mm
Sóng cơ truyền được trong các môi trường
-
A.
khí, chân không và rắn.
-
B.
lỏng, khí và chân không.
-
C.
chân không, rắn và lỏng.
-
D.
rắn, lỏng và khí
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng:
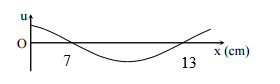
-
A.
\(6cm\)
-
B.
\(12cm\)
-
C.
\(24cm\)
-
D.
\(18cm\)
Một sợi dây đàn hồi rất dài có đầu \(A\) dao động với tần số \(f\) và theo phương vuông góc với sợi dây. Biên độ dao động là \(5cm\), vận tốc truyền sóng trên đây là \(2m/s\). Xét một điểm M trên dây và cách A một đoạn \(12cm\), người ta thấy M luôn luôn dao động lệch pha với A một góc \(\Delta \varphi = (2k + 1)\dfrac{\pi }{2}\) với \(k{\rm{ }} = {\rm{ }}0, \pm 1, \pm 2\). Tính bước sóng \(\lambda \)? Biết tần số \(f\) có giá trị trong khoảng từ \(20{\rm{ }}Hz\) đến \(26{\rm{ }}Hz\).
-
A.
12 cm
-
B.
9,6 cm
-
C.
14 cm
-
D.
16 cm
Phát biểu nào sau đây là đúng khi nói về hiện tượng giao thoa sóng?
-
A.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau.
-
B.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
-
C.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
-
D.
Là hiện tượng hai sóng khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
Phát biểu nào sau đây là sai?
-
A.
Khi xảy ra hiện tượng giao thoa sóng, các gợn sóng có hình các đường hypebol
-
B.
Sóng kết hợp là hai sóng có độ lệch pha biến thiên theo thời gian
-
C.
Điều kiện để xảy ra hiện tượng giao thoa sóng là hai nguồn sóng phải là hai sóng kết hợp
-
D.
Hiện tượng giao thoa sóng xảy ra khi có hai sóng xuất phát từ hai tâm dao động cùng tần số, cùng pha.
Một dây đàn hồi AB đầu A được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết phương trình dao động tại đầu A là \({u_A} = {\rm{ }}acos50\pi t\left( {cm} \right)\). Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ b \((b \ne 0)\) cách đều nhau và cách nhau khoảng \(0,6m\). Giá trị của b và tốc truyền sóng trên sợi dây lần lượt là:
-
A.
\(a\sqrt 2 ;v = 120m/s\)
-
B.
\(a\sqrt 3 ;v = 120m/s\)
-
C.
\(a\sqrt 2 ;v = 60m/s\)
-
D.
\(a\sqrt 3 ;v = 60m/s\)
Phát biểu nào sau đây đúng khi nói về sóng âm
-
A.
Là sóng cơ học truyền được trong tất cả các môi trường rắn, lỏng, khí và chân không
-
B.
Sóng âm trong môi trường lỏng, rắn là sóng ngang
-
C.
Sóng âm không truyền được trong chân không
-
D.
Sóng âm trong môi trường lỏng là sóng ngang
Thuật ngữ âm “trầm” , “bổng” chỉ đặc tính nào của âm dưới đây?
-
A.
Ngưỡng của tai
-
B.
Âm sắc
-
C.
Độ cao
-
D.
Độ to
Có nhiều nguồn âm điểm giống hệt nhau và cùng công suất. Ban đầu tại điểm O đặt \(2\) nguồn âm. Điểm A cách O một khoảng d có thể thay đổi được. Trên tia vuông góc với OA tại A, lấy điểm B cách A khoảng \(9cm\). Điểm M nằm trong đoạn AB sao cho \(AM = 4,5cm\) và góc MOB có giá trị lớn nhất, lúc này mức cường độ âm tại A là \({L_A} = 60dB\). Cần phải đặt thêm tại O bao nhiêu nguồn nữa để mức cường độ âm tại M là \(80dB\)
-
A.
\(298\)
-
B.
\(302\)
-
C.
\(289\)
-
D.
\(131\)
Ở mặt nước, tại hai điểm A và B cách nhau \(8cm\) có hai nguồn giống nhau dao động theo phương thẳng đứng, phát ra hai sóng có bước sóng \(1cm\). M, N là hai điểm thuộc mặt nước cách nhau \(4cm\) và ABMN là hình thang cân (AB // MN). Để trong đoạn MN có đúng \(5\) điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình thang có giá trị nào sau đây?
-
A.
\(6\sqrt 3 c{m^2}\)
-
B.
\(9\sqrt 5 c{m^2}\)
-
C.
\(18\sqrt 5 c{m^2}\)
-
D.
\(18\sqrt 3 c{m^2}\)
Trên một sợi dây đang có sóng dừng với bề rộng của một bụng sóng là \(3 cm\). Biên độ dao động của điểm bụng là
-
A.
\(1,5 cm\).
-
B.
\(0,5 cm\).
-
C.
\(3 cm\).
-
D.
\(0,75 cm\).
Lời giải và đáp án
Một sóng cơ dao động có bước sóng là $λ$. Khoảng cách giữa $n$ ngọn sóng liên tiếp là:
-
A.
$n$ bước sóng
-
B.
$n - 1$ bước sóng
-
C.
$n + 1$ bước sóng
-
D.
$2n$ bước sóng
Đáp án : B
Khoảng cách giữa $n$ ngọn sóng liên tiếp là: $n - 1$ bước sóng
Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục $Ox$. Tại thời điểm $t_0$ một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử $M$ và $O$ dao động lệch pha nhau?

-
A.
\(\dfrac{\pi }{4}ra{\rm{d}}\)
-
B.
\(\dfrac{\pi }{3}ra{\rm{d}}\)
-
C.
\(\dfrac{{3\pi }}{4}ra{\rm{d}}\)
-
D.
\(\dfrac{{2\pi }}{3}ra{\rm{d}}\)
Đáp án : C
+ Sử dụng phương pháp đọc đồ thị dao động sóng
+ Áp dụng biểu thức tính độ lệch pha giữa 2 điểm: \(\Delta \varphi = \dfrac{{2\pi \Delta x}}{\lambda }\)
Từ đồ thị ta có:
+ Bước sóng \(\lambda = 8\) ô
+ Khoảng cách từ O đến M là \(\Delta x = 3\) ô
=> Độ lệch pha giữa M và O là: \(\Delta \varphi = \dfrac{{2\pi x}}{\lambda } = 2\pi .\dfrac{3ô}{8 ô} = \dfrac{{3\pi }}{4}rad\)
Nhận xét nào sau đây là sai khi nói về sóng âm
-
A.
Sóng âm là sóng cơ học truyền được trong cả 3 môi trường rắn, lỏng, khí
-
B.
Trong cả 3 môi trường rắn, lỏng, khí sóng âm luôn là sóng dọc
-
C.
Trong chất rắn sóng âm có cả sóng dọc và sóng ngang
-
D.
Âm thanh có tần số từ 16 Hz đến 20 kHz
Đáp án : B
Sóng âm trong môi trường lỏng, khí là sóng dọc; trong môi trường rắn là sóng dọc hoặc sóng ngang.
Sóng ngang là:
-
A.
Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
-
B.
Sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
-
C.
Sóng trong đó các phần tử của môi trường dao động theo phương song song với phương truyền sóng
-
D.
Sóng trong đó các phần tử của môi trường dao động theo cả hai phương vuông góc và song song với phương truyền
Đáp án : A
Sóng ngang: là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng.
Khi có sóng dừng trên dây, khoảng cách giữa hai nút liên tiếp bằng
-
A.
Một số nguyên lần bước sóng.
-
B.
Một phần tư bước sóng.
-
C.
Một nửa bước sóng.
-
D.
Một bước sóng.
Đáp án : C
Khoảng cách giữa 2 nút hoặc 2 bụng liền kề của sóng dừng là $\dfrac{\lambda }{2}$.
Mối liên hệ giữa bước sóng $λ$, vận tốc truyền sóng $v$, chu kì $T$ và tần số $f$ của một sóng là:
-
A.
\(f = \dfrac{1}{T} = \dfrac{v}{\lambda }\)
-
B.
\(v = \dfrac{1}{f} = \dfrac{T}{\lambda }\)
-
C.
\(\lambda = \dfrac{T}{v} = \dfrac{f}{v}\)
-
D.
\(\lambda = \dfrac{T}{v} = vf\)
Đáp án : A
Vận dụng biểu thức: \(\lambda = \dfrac{v}{f} = vT\)
Ta có: \(\lambda = \dfrac{v}{f} = vT\)
Dùng một âm thoa có tần số rung f = 100Hz người ta tạo ra hai điểm S1,S2 trên mặt nước hai nguồn sóng cùng biên độ,cùng pha.S1S2 = 3,2cm.Tốc độ truyền sóng là 40 cm/s. I là trung điểm của S1S2. Định những điểm dao động cùng pha với I.Tính khoảng từ I đến điểm M gần I nhất dao động cùng pha với I và nằm trên trung trực S1S2 là:
-
A.
1,81cm
-
B.
1,31cm
-
C.
1,20cm
-
D.
1,26cm
Đáp án : C
+ Áp dụng biểu thức xác định bước sóng: \(\lambda = \frac{v}{f}\)
+ Viết phương trình dao động sóng
+ Áp dụng điều kiện dao động cùng pha: \(\Delta \varphi = k2\pi \)
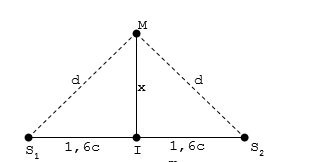
Ta có:
\(\lambda = \frac{v}{f} = 0,4cm\)
- Giả sử phương trình sóng của 2 nguồn là
\({u_{S1}} = {\rm{ }}{u_{S2}} = {\rm{ }}Acos(200\pi t)\)
- Thì phương trình sóng tại I là:
\({u_I} = {u_{1I}} + {u_{2I}} = 2A\cos (200\pi t - 2\pi \frac{{1,6}}{{0,4}}) = 2A\cos (200\pi t - 8\pi ) = 2A\cos (200\pi t)\)
-Tương tự PT sóng tại M cách mỗi nguồn đoạn d ( như hình vẽ ) là:
\({u_M} = 2A\cos (200\pi t - 2\pi \frac{d}{{0,4}})\)
=> Độ lệch pha giữa I và M là
\(\Delta \varphi = 2\pi \frac{d}{{0,4}}\)
để I và M cùng pha thì
\(\Delta \varphi = k2\pi \to d = k.0,4(cm)\)
Theo hình vẽ dễ thấy
\(d > 1,6{\text{ }}cm \to d = k.0,4 > 1,6 \Rightarrow k > 4\)
* Mặt khác cần tìm xmin nên d cũng phải min => k cũng min => kmin=5 => dmin=5.0,4=2cm
${x_{min}} = \sqrt {d_{\min }^2 - 1,{6^2}} = 1,2cm$
Sóng dừng xảy ra trên dây đàn hồi cố định có 1 bụng sóng khi:
-
A.
Chiều dài của dây bằng một phần tư bước sóng.
-
B.
Chiều dài bước sóng gấp đôi chiều dài của dây.
-
C.
Chiều dài của dây bằng bước sóng.
-
D.
Chiều dài bước sóng bằng một số lẻ chiều dài của dây.
Đáp án : B
Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\text{ }}(k \in {N^*})$
Điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\text{ }}(k \in {N^*})$
Có 1 bụng sóng khi k = 1 => λ =2l
Một sóng cơ truyền trên trục Ox trên một dây đàn hồi rất dài với tần số f = 1/3 Hz. Tại thời điểm t0 = 0 và tại thời điểm t1 = 0,875s hình ảnh của sợi dây được mô tả như hình vẽ. Biết rằng: d2 - d1 = 10 cm. Gọi δ là tỉ số giữa tốc độ dao động cực đại của phần tử trên dây và tốc độ truyền sóng. Giá trị của δ là:

-
A.
π
-
B.
\(\dfrac{{3\pi }}{5}\)
-
C.
\(\dfrac{{5\pi }}{3}\)
-
D.
2π
Đáp án : B
+ Đọc đồ thị và áp dụng các công thức sóng cơ học.
+ Sử dụng vòng tròn lượng giác
+ Áp dụng công thức tính độ lệch pha theo không gian và thời gian:
\(\Delta \varphi = \Delta {\varphi _t} + \Delta {\varphi _x} = \omega \Delta t + \dfrac{{2\pi \Delta x}}{\lambda }\)
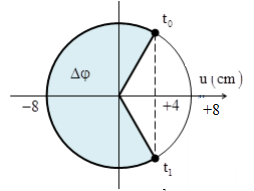
- Biểu diễn trên vòng tròn lượng giác, ta được:
- Độ lệch pha giữa hai điểm cách O các khoảng d1 và d2 như hình vẽ:
\(\begin{array}{l}\Delta \varphi = \Delta {\varphi _t} + \Delta {\varphi _x} = 2\pi f\Delta t + \dfrac{{2\pi \Delta d}}{\lambda } = {240^0} = \dfrac{{4\pi }}{3}\\ \\\leftrightarrow \dfrac{{7\pi }}{{12}} + \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{4\pi }}{3} \\\to \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{3\pi }}{4} \\\to \lambda = \dfrac{{8\Delta d}}{3} = \dfrac{{8.10}}{3} = \dfrac{{80}}{3}cm\end{array}\)
Tỉ số giữa tốc độ dao động cực đại của phần tử trên dây và tốc độ truyền sóng:
\(\delta = \dfrac{{\omega A}}{v} = \dfrac{{\omega A}}{{\lambda f}} = \dfrac{{\omega A}}{{\lambda \dfrac{\omega }{{2\pi }}}} = \dfrac{{2\pi A}}{\lambda } = \dfrac{{2\pi 8}}{{\dfrac{{80}}{3}}} = \dfrac{{3\pi }}{5}\)
Tại hai điểm A, B trong môi trường truyền sóng có hai nguồn kết hợp dao động cùng phương với phương trình lần lượt là : ${u_A} = a.cos(\omega t)(cm)$ và ${u_B} = a.cos(\omega t + \pi )(cm)$. Biết vận tốc và biên độ do mỗi nguồn truyền đi không đổi trong quá trình truyền sóng. Trong khoảng giữa Avà B có giao thoa sóng do hai nguồn trên gây ra. Phần tử vật chất tại trung điểm O của đoạn AB dao động với biên độ bằng :
-
A.
a/2
-
B.
2a
-
C.
0
-
D.
a
Đáp án : C
Sử dụng công thức tính biên độ tại 1 điểm bất kì trong trường giao thoa với 2 nguồn ngược pha nhau:
\(a = 2A\left| {c{\text{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{\pi }{2}} \right)} \right|\)
Theo giả thiết nhìn vào phương trình sóng ta thấy hai nguồn dao động ngược pha nên tại O là trung điểm của AB sẽ dao động với biên độ cực tiểu ${a_M} = 0$
Một sợi dây $AB$ dài $100 cm$ căng ngang, đầu $B$ cố định, đầu $A$ gắn với một nhánh của âm thoa dao động điều hòa với tần số $40 Hz$. Trên dây $AB$ có một sóng dừng ổn định, $A$ được coi là nút sóng. Tốc độ truyền sóng trên dây là $20 m/s$. Tìm số nút sóng và bụng sóng trên dây, kể cả $A$ và $B$.
-
A.
$3$ bụng và $4$ nút
-
B.
$4$ bụng và $4$ nút
-
C.
$4$ bụng và $5$ nút
-
D.
$5$ bụng và $5$ nút
Đáp án : C
+ Sử dụng công thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ;
Số nút sóng = k + 1
Ta có:
\(\lambda = \dfrac{v}{f} = 0.5{\text{ }}m = 50{\text{ }}cm.\)
Ta có điều kiện để có sóng dừng trên dây hai đầu cố định:
$l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ;
Số nút sóng = k + 1
Trên dây có:
\(k = \dfrac{{AB}}{{\dfrac{\lambda }{2}}} = \dfrac{{2AB}}{\lambda } = 4\) bụng sóng.
=> số nút = k + 1 = 5 nút sóng
Một sợi dây đàn hồi nằm ngang có điểm đầu O dao động theo phương thẳng đứng với biên độ A = 5cm, T = 0,5s. Vận tốc truyền sóng là 40cm/s. Viết phương trình sóng tại M cách O d = 50 cm.
-
A.
\({u_M} = 5\cos (4\pi t - 5\pi )(cm)\)
-
B.
\({u_M} = 5\cos (4\pi t - 2,5\pi )(cm)\)
-
C.
\({u_M} = 5\cos (4\pi t + \pi )(cm)\)
-
D.
\({u_M} = 5\cos (4\pi t - 25\pi )(cm)\)
Đáp án : A
+ Áp dụng công thức tính bước sóng: \(\lambda = vT\)
+ Áp dụng công thức tính tần số góc: \(\omega = \frac{{2\pi }}{T}\)
+ Viết phương trình dao động của một điểm
Bước sóng:
\(\lambda = vT = 40.0,5 = 20cm\)
Tần số góc:
\(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,5}} = 4\pi ra{\rm{d}}/s\)
PT sóng tại M:
\({u_M} = 5c{\rm{os}}\left( {4\pi t - \frac{{2\pi d}}{\lambda }} \right) = 5c{\rm{os}}\left( {4\pi t - \frac{{2\pi .50}}{{20}}} \right) = 5c{\rm{os}}\left( {4\pi t - 5\pi } \right)\)
Một dây đàn dài $15cm$, khi gảy phát ra âm cơ bản với tốc độ truyền sóng trên dây là $300m/s$. Tốc độ truyền âm trong không khí là $340m/s$. Bước sóng của âm phát ra trong không khí là:
-
A.
$0,5m$
-
B.
$1,24m$
-
C.
$0,34m$
-
D.
$0,68m$
Đáp án : C
+ Sử dụng công thức chiều dài dây đàn: $l = k\dfrac{\lambda }{2}$
+ Sử dụng công thức tính bước sóng: $\lambda = \dfrac{v}{f}$
Ta có, chiều dài của dây đàn:
$l = k\dfrac{\lambda }{2} = k\dfrac{v}{{2f}} \to f = k\dfrac{v}{{2l}}$
Âm cơ bản là âm ứng với $k=1$
=> Tần số của âm cơ bản:
${f_1} = \dfrac{v}{{2l}} = \dfrac{{300}}{{2.0,15}} = 1000H{\text{z}}$
=> Bước sóng của âm phát ra trong không khí:
$\lambda = \dfrac{{{v_{kk}}}}{{{f_1}}} = \dfrac{{340}}{{1000}} = 0,34m$
Giao thoa sóng nước với hai nguồn giống hệt nhau A, B cách nhau 20cm có tần số 50Hz. Tốc độ truyền sóng trên mặt nước là 1,5m/s. Trên mặt nước xét đường tròn tâm A, bán kính AB. Điểm trên đường tròn dao động với biên độ cực đại cách đường thẳng qua A, B một đoạn gần nhất là:
-
A.
18,67mm
-
B.
17,96mm
-
C.
19,97mm
-
D.
15,34mm
Đáp án : C
Áp dụng điều kiện dao động cực đại của 2 nguồn cùng pha: d2 - d1 = kλ

\( = > h = \sqrt {d_2^2 - {x^2}} = \sqrt {{{20}^2} - 1} = \sqrt {399} = 19,97mm\)
Sóng cơ truyền được trong các môi trường
-
A.
khí, chân không và rắn.
-
B.
lỏng, khí và chân không.
-
C.
chân không, rắn và lỏng.
-
D.
rắn, lỏng và khí
Đáp án : D
Sóng cơ chỉ truyền được trong các môi trường rắn , lỏng, khí
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng:

-
A.
\(6cm\)
-
B.
\(12cm\)
-
C.
\(24cm\)
-
D.
\(18cm\)
Đáp án : B
Đọc đồ thị li độ u - x
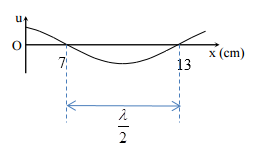
Từ đồ thị,
Ta có: \(\frac{\lambda }{2} = 13 - 7 = 6cm \to \lambda = 12cm\)
Một sợi dây đàn hồi rất dài có đầu \(A\) dao động với tần số \(f\) và theo phương vuông góc với sợi dây. Biên độ dao động là \(5cm\), vận tốc truyền sóng trên đây là \(2m/s\). Xét một điểm M trên dây và cách A một đoạn \(12cm\), người ta thấy M luôn luôn dao động lệch pha với A một góc \(\Delta \varphi = (2k + 1)\dfrac{\pi }{2}\) với \(k{\rm{ }} = {\rm{ }}0, \pm 1, \pm 2\). Tính bước sóng \(\lambda \)? Biết tần số \(f\) có giá trị trong khoảng từ \(20{\rm{ }}Hz\) đến \(26{\rm{ }}Hz\).
-
A.
12 cm
-
B.
9,6 cm
-
C.
14 cm
-
D.
16 cm
Đáp án : B
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Áp dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
Độ lệch pha:
\(\begin{array}{l}\Delta \varphi = (2k + 1)\dfrac{\pi }{2} = \dfrac{{2\pi d}}{\lambda }\\ \to f = \left( {2k + 1} \right)\dfrac{v}{{4d}}\end{array}\)
Mặt khác: \(20{\rm{ }}Hz < f < 26{\rm{ }}Hz\)
\(\begin{array}{l} \to 20 < f = \left( {2k + 1} \right)\dfrac{v}{{4d}} < 26\\ \leftrightarrow 20 < \left( {2k + 1} \right)\dfrac{2}{{4.0,12}} < 26\\ \to 1,9 < k < 2,62\\ \to k = 2\\ \to f = \left( {2.2 + 1} \right)\dfrac{2}{{4.0,12}} = \dfrac{125}{6}H{\rm{z}}\\ \to \lambda = \dfrac{v}{f} = \dfrac{2}{\dfrac{125}{6}} = 0,096m = 9,6cm\end{array}\)
Phát biểu nào sau đây là đúng khi nói về hiện tượng giao thoa sóng?
-
A.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau.
-
B.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
-
C.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
-
D.
Là hiện tượng hai sóng khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
Đáp án : C
Hiện tượng giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
Phát biểu nào sau đây là sai?
-
A.
Khi xảy ra hiện tượng giao thoa sóng, các gợn sóng có hình các đường hypebol
-
B.
Sóng kết hợp là hai sóng có độ lệch pha biến thiên theo thời gian
-
C.
Điều kiện để xảy ra hiện tượng giao thoa sóng là hai nguồn sóng phải là hai sóng kết hợp
-
D.
Hiện tượng giao thoa sóng xảy ra khi có hai sóng xuất phát từ hai tâm dao động cùng tần số, cùng pha.
Đáp án : B
Ta có:
+ Hai sóng là hai sóng kết hợp tức là hai sóng cùng tần số và có độ lệch pha không đổi theo thời gian (hoặc hai sóng cùng pha).
+ Hiện tượng giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
+ Các gợn sóng có hình các đường hypebol gọi là các vân giao thoa
=> Các phương án:
+ A, C, D – đúng
+ B – sai vì: Sóng kết hợp là sóng có cùng tần số và có độ lệch pha không đổi theo thời gian
Một dây đàn hồi AB đầu A được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết phương trình dao động tại đầu A là \({u_A} = {\rm{ }}acos50\pi t\left( {cm} \right)\). Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ b \((b \ne 0)\) cách đều nhau và cách nhau khoảng \(0,6m\). Giá trị của b và tốc truyền sóng trên sợi dây lần lượt là:
-
A.
\(a\sqrt 2 ;v = 120m/s\)
-
B.
\(a\sqrt 3 ;v = 120m/s\)
-
C.
\(a\sqrt 2 ;v = 60m/s\)
-
D.
\(a\sqrt 3 ;v = 60m/s\)
Đáp án : C
+ Sử dụng vòng tròn lượng giác
+ Áp dụng công thức tính tốc độ truyền sóng: v = lf
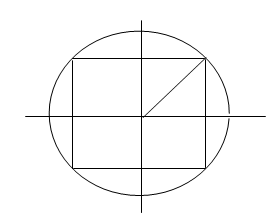
Các điểm dao động với biên độ \(b \ne 0\) và \(b \ne 2a\) (tức là không phải là điểm nút và điểm bụng) cách đều nhau thì khoảng cách giữa hai điểm bằng \(\frac{\lambda }{4} = 0,6m \to \lambda = 2,4m\)
Do đó: \(v = \lambda f = \lambda .\frac{\omega }{{2\pi }} = 2,4.\frac{{50}}{{2\pi }} = 60m/s\)
Theo hình vẽ ta thấy: \(b = \frac{{2a\sqrt 2 }}{2} = a\sqrt 2 \)
(Biên độ của bụng sóng là 2a)
Phát biểu nào sau đây đúng khi nói về sóng âm
-
A.
Là sóng cơ học truyền được trong tất cả các môi trường rắn, lỏng, khí và chân không
-
B.
Sóng âm trong môi trường lỏng, rắn là sóng ngang
-
C.
Sóng âm không truyền được trong chân không
-
D.
Sóng âm trong môi trường lỏng là sóng ngang
Đáp án : C
A – sai vì: sóng âm không truyền được trong chân không
B – sai vì: sóng âm trong môi trường lỏng, khí là sóng dọc
C – đúng
D – sai vì: sóng âm trong môi trường lỏng là sóng dọc
Thuật ngữ âm “trầm” , “bổng” chỉ đặc tính nào của âm dưới đây?
-
A.
Ngưỡng của tai
-
B.
Âm sắc
-
C.
Độ cao
-
D.
Độ to
Đáp án : C
Ta có độ cao phụ thuộc vào tần số của âm.
Tần số lớn \( \to \) âm bổng
Tần số nhỏ \( \to \) âm trầm
Có nhiều nguồn âm điểm giống hệt nhau và cùng công suất. Ban đầu tại điểm O đặt \(2\) nguồn âm. Điểm A cách O một khoảng d có thể thay đổi được. Trên tia vuông góc với OA tại A, lấy điểm B cách A khoảng \(9cm\). Điểm M nằm trong đoạn AB sao cho \(AM = 4,5cm\) và góc MOB có giá trị lớn nhất, lúc này mức cường độ âm tại A là \({L_A} = 60dB\). Cần phải đặt thêm tại O bao nhiêu nguồn nữa để mức cường độ âm tại M là \(80dB\)
-
A.
\(298\)
-
B.
\(302\)
-
C.
\(289\)
-
D.
\(131\)
Đáp án : A
+ Sử dụng công thức \(\tan ({\alpha _1} - {\alpha _2}) = \frac{{\tan {\alpha _1} - \tan {\alpha _2}}}{{1 + \tan {\alpha _1}\tan {\alpha _2}}}\) và BĐT côsi
+ Sử dụng công thức :Hiệu mức cường độ âm: \({L_A} - {L_M} = 10\log \frac{{{I_A}}}{{{I_M}}}\)
+ Sử dụng công thức tính cường độ âm: \(I = \frac{{2P}}{{4\pi {R^2}}}\)
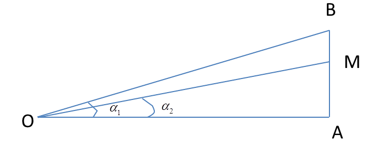
\(\begin{array}{l}\begin{array}{*{20}{l}}{OA = dm}\\{AB = {\rm{ 9}}m}\end{array}\\AM{\rm{ }} = 4,5m\end{array}\)
\(\begin{array}{l}\tan \angle MOB = \tan ({\alpha _1} - {\alpha _2}) = \frac{{\tan {\alpha _1} - \tan {\alpha _2}}}{{1 + \tan {\alpha _1}\tan {\alpha _2}}}\\ = \frac{{\frac{9}{d} - \frac{{4,5}}{d}}}{{1 + \frac{9}{d}.\frac{{4,5}}{d}}} = \frac{{4,5}}{{d + \frac{{81}}{{2d}}}}\end{array}\)
+ Theo BĐT Cosi, ta có:
\(d + \frac{{81}}{{2d}} \ge 2\sqrt {\frac{{81}}{2}} = 9\sqrt 2 \)
Dấu “=” xảy ra khi: \(d = \frac{{81}}{2}d \to d = 4,5\sqrt 2 m\)
Do đó: \(OM = \sqrt {{{(4,5\sqrt 2 )}^2} + 4,{5^2}} = 4,5\sqrt 3 m\)
+ Ta có:
\(\begin{array}{l}{L_A} - {L_M} = 10\log \frac{{{I_A}}}{{{I_M}}}\\ \leftrightarrow 60 - 80 = - 20 = 10\log \frac{{{I_A}}}{{{I_M}}}\\ \to \frac{{{I_A}}}{{{I_M}}} = 0,01\end{array}\)
Mặt khác:
\(\begin{array}{l}\left\{ \begin{array}{l}{I_A} = \frac{{2P}}{{4\pi R_A^2}}\\{I_M} = \frac{{(x + 2)P}}{{4\pi R_M^2}}\end{array} \right.\\ \to \frac{{{I_A}}}{{{I_M}}} = \frac{2}{{x + 2}}\frac{{R_M^2}}{{R_A^2}} = \frac{2}{{x + 2}}\frac{{{{\left( {4,5\sqrt 3 } \right)}^2}}}{{{{\left( {4,5\sqrt 2 } \right)}^2}}} = 0,01\\ \to x = 298\end{array}\)
Ở mặt nước, tại hai điểm A và B cách nhau \(8cm\) có hai nguồn giống nhau dao động theo phương thẳng đứng, phát ra hai sóng có bước sóng \(1cm\). M, N là hai điểm thuộc mặt nước cách nhau \(4cm\) và ABMN là hình thang cân (AB // MN). Để trong đoạn MN có đúng \(5\) điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình thang có giá trị nào sau đây?
-
A.
\(6\sqrt 3 c{m^2}\)
-
B.
\(9\sqrt 5 c{m^2}\)
-
C.
\(18\sqrt 5 c{m^2}\)
-
D.
\(18\sqrt 3 c{m^2}\)
Đáp án : C
Tại M dao động cực đại nên d2 – d1 = kλ
Để trên MN có đúng 5 điểm cực đại thì M và N nằm trên các đường cực đại bậc 2
NB – NA = 2λ = 2cm
\( \Rightarrow \sqrt {H{B^2} + N{H^2}} - \sqrt {H{A^2} + N{H^2}} = 2 \\\Rightarrow \sqrt {{6^2} + N{H^2}} - \sqrt {{2^2} + N{H^2}} = 2cm \\\Rightarrow NH = 3\sqrt{5} cm\)
Diện tích hình thang :
\(S = \dfrac{{AB + MN}}{2}.NH = \dfrac{{8 + 4}}{2}.3\sqrt{5}=18\sqrt 5 c{m^2}\)
Trên một sợi dây đang có sóng dừng với bề rộng của một bụng sóng là \(3 cm\). Biên độ dao động của điểm bụng là
-
A.
\(1,5 cm\).
-
B.
\(0,5 cm\).
-
C.
\(3 cm\).
-
D.
\(0,75 cm\).
Đáp án : A
Biên độ dao động của điểm bụng bằng \(\dfrac{1}{2}\)bề rộng của bụng sóng.
Biên độ dao động của điểm bụng bằng \(\dfrac{1}{2}\) bề rộng của bụng sóng. \(A = \dfrac{3}{2} = 1,5(cm)\)
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận