Đề kiểm tra 1 tiết chương 2: Sóng cơ và sóng âm - Đề số 02
Đề bài
Nguồn sóng ở O dao động với tần số 10Hz, dao động truyền đi với vận tốc 0,4m/s theo phương Oy; trên phương này có hai điểm P và Q với PQ = 15cm. Biên độ sóng bằng a = 1cm và không thay đổi khi lan truyền . Nếu tại thời điểm t nào đó P có li độ 1cm thì li độ tại Q là:
-
A.
1cm
-
B.
-1cm
-
C.
0 cm
-
D.
2cm
Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng có dạng như hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó, điểm N đang chuyển động:
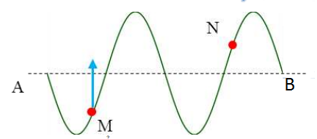
-
A.
Đi xuống
-
B.
Đứng yên
-
C.
Chạy ngang
-
D.
Đi lên
Biểu thức nào sau đây xác định vị trí các cực đại giao thoa với 2 nguồn cùng pha?
-
A.
\({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda \)
-
B.
\({d_2} - {d_1} = \frac{{k\lambda }}{2}\)
-
C.
\({d_2} - {d_1} = k\lambda \)
-
D.
\({d_2} - {d_1} = \left( {k - \frac{1}{2}} \right)\lambda \)
Trên một sợi dây có chiều dài l , hai đầu cố định, đang có sóng dừng. Trên dây có một bụng sóng. Biết vận tốc truyền sóng trên dây là v không đổi. Tần số của sóng là:
-
A.
$\dfrac{v}{{2\ell }}$
-
B.
$\dfrac{v}{{4\ell }}$
-
C.
$\dfrac{{2v}}{\ell }$
-
D.
$\dfrac{v}{\ell }$
Hai âm có âm sắc khác nhau là do chúng có:
-
A.
Cường độ khác nhau
-
B.
Các hoạ âm có tần số và biên độ khác nhau
-
C.
Biên độ khác nhau
-
D.
Tần số khác nhau
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 24 cm, dao động theo phương thẳng đứng với phương trình là uA=uB=acos60πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là v=45cm/s. Gọi MN=4cm là đoạn thẳng trên mặt chất lỏng có chung trung trực với AB. Khoảng cách xa nhất giữa MN với AB là bao nhiêu để có ít nhất 5 điểm dao động cực đại nằm trên MN?
-
A.
12,7 cm
-
B.
10,5 cm
-
C.
14,2 cm
-
D.
6,4 cm
Một sóng có tần số $500 Hz$ và tốc độ lan truyền $350 m/s$. Hỏi hai điểm gần nhất trên phương truyền sóng cách nhau một khoảng bao nhiêu để giữa chúng có độ lệch pha \(\dfrac{\pi }{4}\)?
-
A.
$8,75 cm$
-
B.
$17,5 cm$
-
C.
$35 cm$
-
D.
$70 cm$
Khi nói về sóng cơ, phát biểu nào sau đây sai?
-
A.
Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó ngược pha nhau.
-
B.
Sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng gọi là sóng dọc.
-
C.
Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng gọi là sóng ngang.
-
D.
Tại mỗi điểm của môi trường có sóng truyền qua, biên độ của sóng là biên độ dao động của phần tử môi trường.
Trên một sợi dây đàn hồi có 3 điểm M, N và P là trung điểm của đoạn MB. Trên dây có sóng lan truyền từ M đến P với chu kì T (T > 0,5s). Hình vẽ bên mô tả hình dạng của sợi dây ở thời điểm t1 (nét liền) và t2 = t1 + 0,5s (nét đứt). M, N và P lần lượt là các vị trí cân bằng tương ứng. Lấy \(2\sqrt {11} = 6,6\) và coi biên độ sóng không đổi khi truyền đi. Tại thời điểm \({t_0} = {\rm{ }}{t_1} - \frac{1}{9}s\) vận tốc dao động của phần tử dây tại N là:
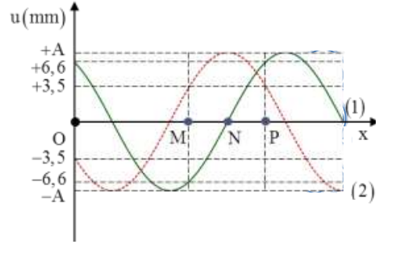
-
A.
3,53 cm/s
-
B.
-3,53 cm/s
-
C.
4,98 cm/s
-
D.
-4,98 cm/s
Một sợi dây đàn hồi rất dài có đầu $A$ dao động với tần số $f$ và theo phương vuông góc với sợi dây. Biên độ dao động là $4 cm$, vận tốc truyền sóng trên dây là $4 (m/s)$. Xét một điểm $M$ trên dây và cách $A$ một đoạn $28 cm$, người ta thấy M luôn luôn dao động lệch pha với $A$ một góc \(\Delta \varphi = (2k + 1)\dfrac{\pi }{2}\) với $k = 0, ±1, ±2,....$. Tính bước sóng $λ$? Biết tần số $f$ có giá trị trong khoảng từ $22 Hz$ đến $26 Hz$.
-
A.
$12 cm$
-
B.
$8 cm$
-
C.
$14 cm$
-
D.
$16 cm$
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, $A$ là một điểm nút, $B$ là một điểm bụng gần $A$ nhất, $C$ là trung điểm của $AB$, với $AC = 10cm$. Biết khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại $B$ bằng biên độ dao động của phần tử tại $C$ là $0,1s$. Tốc độ truyền sóng trên dây là:
-
A.
$2 m/s$
-
B.
$0,5 m/s$
-
C.
$0,25 m/s$
-
D.
$1 m/s$
Chọn câu sai.
-
A.
Sóng ngang có phương dao động vuông góc với phương truyền sóng.
-
B.
Sóng cơ cũng làm lan truyền vật chất trên phương truyền sóng.
-
C.
Sóng cơ truyền trong chất khí là sóng dọc.
-
D.
Bước sóng là quãng đường sóng truyền được trong thời gian bằng một chu kì sóng.
Chọn phát biểu sai khi nói về tốc độ truyền sóng trong một môi trường:
-
A.
Là tốc độ lan truyền dao động trong môi trường
-
B.
Phụ thuộc vào tính đàn hồi và mật độ môi trường
-
C.
Là vận tốc dao động của các phần tử vật chất khi sóng truyền qua
-
D.
\({v_R} > {v_L} > {v_K}\)
Một sóng cơ dao động có bước sóng là \(\lambda \). Khoảng cách giữa 5 ngọn sóng liên tiếp là:
-
A.
\(5\lambda \)
-
B.
\(6\lambda \)
-
C.
\(4\lambda \)
-
D.
\(10\lambda \)
Một sóng hình sin đang truyền trên một sợi dây, theo chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây ở các thời điểm \({t_1}\) và \({t_2} = {\rm{ }}{t_1} + {\rm{ }}0,7s\). Chu kì của sóng là:
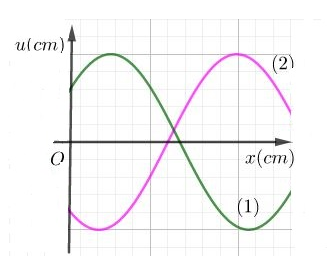
-
A.
0,7 s
-
B.
0,35 s
-
C.
0,8 s
-
D.
1,6 s
Phát biểu nào sau đây là đúng khi nói về hiện tượng giao thoa sóng?
-
A.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau.
-
B.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
-
C.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
-
D.
Là hiện tượng hai sóng khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
Khi có sóng dừng trên dây, khoảng cách giữa hai bụng sóng liên tiếp bằng bao nhiêu? Biết sóng truyền trên dây có bước sóng \(\lambda = 4m\)
-
A.
\(4k\left( m \right)\) với \(k \in Z\)
-
B.
\(1\left( m \right)\)
-
C.
\(2\left( m \right)\)
-
D.
\(4\left( m \right)\)
Một sợi dây AB dài\(60{\rm{ }}cm\). Đầu A dao động với tần số \(f{\rm{ }} = {\rm{ }}50{\rm{ }}Hz\). Đầu B cố định. Trên dây AB có một sóng dừng ổn định, A được coi là nút sóng. Tốc độ truyền sóng trên dây là \(60cm/s\). Hỏi điểm M cách A một khoảng \(3cm\) là nút hay bụng thứ mấy kể từ A và trên dây có bao nhiêu nút, bao nhiêu bụng kể cả A và B.
-
A.
M là nút số 6, trên dây có 100 nút - 100 bụng.
-
B.
M là bụng số 6, trên dây có 100 nút - 100 bụng.
-
C.
M là nút số 6, trên dây có 101 nút - 100 bụng.
-
D.
M là bụng số 6, trên dây có 101 nút - 100 bụng.
Vận tốc truyền âm phụ thuộc vào các yếu tố
-
A.
Cường độ âm, độ to của âm
-
B.
Tính đàn hồi, mật độ môi trường và nhiệt độ của môi trường
-
C.
Tần số âm và nhiệt độ môi trường
-
D.
Tần số âm và cường to của âm
Chọn phương án đúng trong các phương án dưới đây:
-
A.
Đối với tai con người, cường độ âm càng lớn thì âm càng nhỏ
-
B.
Cảm giác nghe cao hay thấp chỉ phụ thuộc vào cường độ âm
-
C.
Cùng một cường độ âm tai con người nghe âm cao to hơn nghe âm trầm
-
D.
Độ to là đặc trưng vật lí phụ thuộc vào tần số âm và mức cường độ âm
Một dây đàn dài 12cm, khi gãy phát ra âm cơ bản với tốc độ truyền sóng trên dây là 270m/s. Tốc độ truyền âm trong không khí là 340m/s. Bước sóng của âm phát ra trong không khí là:
-
A.
0,3m
-
B.
0,076m
-
C.
0,15m
-
D.
0,6m
Một người đứng cách một bức tường 30 m nghe một tiếng súng nổ. Vị trí đặt súng cách tường 165 m. Người và súng cùng trên đường thẳng vuông góc với tường. Sau khi nghe tiếng nổ, người này lại nghe tiếng nổ do âm thanh phản xạ trên bức tường. Tốc độ âm thanh trong không khí là 330 m/s. Khoảng thời gian giữa hai tiếng nổ là:
-
A.
\(\frac{1}{3}s\)
-
B.
\(\frac{3}{{11}}s\)
-
C.
\(\frac{1}{{11}}s\)
-
D.
\(\frac{2}{{11}}s\)
Trên mặt nước tại hai điểm \({S_1},{\rm{ }}{S_2}\) người ta đặt hai nguồn sóng cơ kết hợp, dao động điều hoà theo phương thẳng đứng với phương trình \({u_A} = 6cos50\pi t\) và \({u_B} = 8cos50\pi t\) (\({u_A}\) và \({u_B}\) tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt nước là \(40cm/s\), coi biên độ sóng không đổi khi truyền đi. Trên đoạn thẳng \({S_1}{S_2}\), điểm dao động với biên độ \(1cm\) và cách trung điểm của đoạn \({S_1}{S_2}\) một đoạn gần nhất là:
-
A.
0,25 cm
-
B.
0,5 cm
-
C.
0,197 cm
-
D.
1 cm
Tại điểm \(O\) đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm \(A\) cách \(O\) một đoạn \(d\) (\(m\)) có mức cường độ âm là \(L_A = 40 dB\). Trên tia vuông góc với \(OA\) tại \(A\), lấy điểm \(B\) cách \(A\) một khoảng \(6 m\). Điểm \(M\) thuộc đoạn \(AB\) sao cho \(AM = 4,5 m\) và góc \(\widehat {MOB}\)có giá trị lớn nhất. Để mức cường độ âm tại \(M\) là \(50 dB\) thì cần đặt thêm tại \(O\) bao nhiêu nguồn âm nữa?
-
A.
\(35\)
-
B.
\(25\)
-
C.
\(15\)
-
D.
\(33\)
Hiện tượng giao thoa ánh sáng chứng tỏ rằng ánh sáng
-
A.
là sóng ngang.
-
B.
có bản chất sóng.
-
C.
gồm các hạt phôtôn.
-
D.
là sóng dọc.
Lời giải và đáp án
Nguồn sóng ở O dao động với tần số 10Hz, dao động truyền đi với vận tốc 0,4m/s theo phương Oy; trên phương này có hai điểm P và Q với PQ = 15cm. Biên độ sóng bằng a = 1cm và không thay đổi khi lan truyền . Nếu tại thời điểm t nào đó P có li độ 1cm thì li độ tại Q là:
-
A.
1cm
-
B.
-1cm
-
C.
0 cm
-
D.
2cm
Đáp án : C
+ Áp dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\)
+ Vận dụng công thức tính độ lệch pha: \(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda }\)
+ Sử dụng vòng tròn lượng giác.
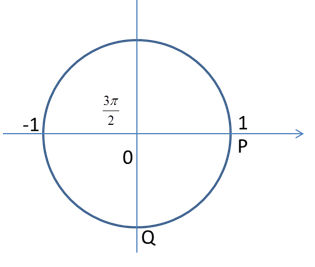
Ta có:
\(\lambda = \frac{v}{f} = \frac{{0,4}}{{10}} = 0,04m = 4cm\)
Độ lệch pha giữa hai điểm P và Q là:
\(\Delta \varphi = \frac{{2\pi \Delta d}}{\lambda } = \frac{{2\pi 15}}{4} = \frac{{15\pi }}{2} = 6\pi + \frac{{3\pi }}{2}\)
Từ vòng tròn lượng giác, ta có li độ tại Q là 0cm
Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng có dạng như hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó, điểm N đang chuyển động:

-
A.
Đi xuống
-
B.
Đứng yên
-
C.
Chạy ngang
-
D.
Đi lên
Đáp án : D
Theo phương truyền sóng, các phần tử trước đỉnh sóng sẽ đi xuống, sau đỉnh sóng sẽ đi lên.
Từ đồ thị ta có, điểm M sau đỉnh sóng đang đi lên
=> Sóng truyền từ B đến A và N cũng đang đi lên
Biểu thức nào sau đây xác định vị trí các cực đại giao thoa với 2 nguồn cùng pha?
-
A.
\({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda \)
-
B.
\({d_2} - {d_1} = \frac{{k\lambda }}{2}\)
-
C.
\({d_2} - {d_1} = k\lambda \)
-
D.
\({d_2} - {d_1} = \left( {k - \frac{1}{2}} \right)\lambda \)
Đáp án : C
Vị trí các cực đại giao thoa với 2 nguồn cùng pha (∆φ = 0): \({d_2} - {d_1} = k\lambda \)
Trên một sợi dây có chiều dài l , hai đầu cố định, đang có sóng dừng. Trên dây có một bụng sóng. Biết vận tốc truyền sóng trên dây là v không đổi. Tần số của sóng là:
-
A.
$\dfrac{v}{{2\ell }}$
-
B.
$\dfrac{v}{{4\ell }}$
-
C.
$\dfrac{{2v}}{\ell }$
-
D.
$\dfrac{v}{\ell }$
Đáp án : A
Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Điều kiện để có sóng dừng trên dây hai đầu cố định:
$l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k=1
$l = \dfrac{\lambda }{2}{\text{ = }}\dfrac{v}{{2f}} \to f = \dfrac{v}{{2l}}$
Hai âm có âm sắc khác nhau là do chúng có:
-
A.
Cường độ khác nhau
-
B.
Các hoạ âm có tần số và biên độ khác nhau
-
C.
Biên độ khác nhau
-
D.
Tần số khác nhau
Đáp án : B
Hai âm có âm sắc khác nhau khi chúng có các họa âm có tần số và biên độ khác nhau
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 24 cm, dao động theo phương thẳng đứng với phương trình là uA=uB=acos60πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là v=45cm/s. Gọi MN=4cm là đoạn thẳng trên mặt chất lỏng có chung trung trực với AB. Khoảng cách xa nhất giữa MN với AB là bao nhiêu để có ít nhất 5 điểm dao động cực đại nằm trên MN?
-
A.
12,7 cm
-
B.
10,5 cm
-
C.
14,2 cm
-
D.
6,4 cm
Đáp án : B
+ Áp dụng biểu thức xác định bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Áp dụng điều kiện dao động cực đại của 2 nguồn cùng pha: d2 - d1 = kλ
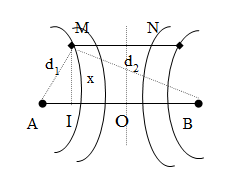
Bước sóng \(\lambda = \dfrac{v}{f} = \dfrac{{45}}{{30}} = 1,5cm\)
Muốn trên MN có ít nhất 5 điểm dao động với biên độ cực đại thì M và N phải thuộc đường cực đại thứ 2 tính từ cực đại trung tâm.
Xét M ta có \({d_2} - {d_1} = 2\lambda = 2.1,5 = 3cm\) (1) (cực đại thứ 2 nên k=2)
Ta có : \(OA = OB = \dfrac{{AB}}{2} = \dfrac{{24}}{2} = 12cm\)
\(OI = \dfrac{{MN}}{2} = \dfrac{4}{2} = 2cm\)
\( \Rightarrow \left\{ \begin{array}{l}BI = OB + OI = 12 + 2 = 14cm\\AI = AB - BI = 24 - 14 = 10cm\end{array} \right.\)
Suy ra : \(\left\{ \begin{array}{l}{d_2} = \sqrt {M{I^2} + B{I^2}} = \sqrt {{x^2} + {{14}^2}} \\{d_1} = \sqrt {M{I^2} + A{I^2}} = \sqrt {{x^2} + {{10}^2}} \end{array} \right.\)
Thay vào (1), ta được :
\(\begin{array}{l}\sqrt {{x^2} + {{14}^2}} - \sqrt {{x^2} + {{10}^2}} = 3\\ \Rightarrow x = 10,5cm\end{array}\)
Một sóng có tần số $500 Hz$ và tốc độ lan truyền $350 m/s$. Hỏi hai điểm gần nhất trên phương truyền sóng cách nhau một khoảng bao nhiêu để giữa chúng có độ lệch pha \(\dfrac{\pi }{4}\)?
-
A.
$8,75 cm$
-
B.
$17,5 cm$
-
C.
$35 cm$
-
D.
$70 cm$
Đáp án : A
+ Áp dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Bước sóng:
\(\lambda = \dfrac{v}{f} = \dfrac{{350}}{{500}} = 0,7m\)
Để độ lệch pha giữa 2 điểm gần nhất là \(\dfrac{\pi }{4}\)
\( \leftrightarrow \Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{\pi }{4} \to d = \dfrac{\lambda }{8} = \dfrac{{0,7}}{8} = 0,0875m = 8,75cm\)
Khi nói về sóng cơ, phát biểu nào sau đây sai?
-
A.
Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó ngược pha nhau.
-
B.
Sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng gọi là sóng dọc.
-
C.
Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng gọi là sóng ngang.
-
D.
Tại mỗi điểm của môi trường có sóng truyền qua, biên độ của sóng là biên độ dao động của phần tử môi trường.
Đáp án : A
A - sai vì: Bước sóng $\lambda $ là khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng dao động cùng pha
Trên một sợi dây đàn hồi có 3 điểm M, N và P là trung điểm của đoạn MB. Trên dây có sóng lan truyền từ M đến P với chu kì T (T > 0,5s). Hình vẽ bên mô tả hình dạng của sợi dây ở thời điểm t1 (nét liền) và t2 = t1 + 0,5s (nét đứt). M, N và P lần lượt là các vị trí cân bằng tương ứng. Lấy \(2\sqrt {11} = 6,6\) và coi biên độ sóng không đổi khi truyền đi. Tại thời điểm \({t_0} = {\rm{ }}{t_1} - \frac{1}{9}s\) vận tốc dao động của phần tử dây tại N là:

-
A.
3,53 cm/s
-
B.
-3,53 cm/s
-
C.
4,98 cm/s
-
D.
-4,98 cm/s
Đáp án : B
+ Đọc đồ thị và áp dụng các công thức sóng cơ học.
+ Viết phương trình dao động sóng
+ Áp dụng công thức tính khoảng cách giữa hai phần tử sóng: \(d = \sqrt {{x^2} + \Delta {u^2}} \)
Từ đồ thị ta thấy rằng 2 thời điểm t1 và t2 vuông pha nhau, do đó:
\(\Delta \varphi = \omega \Delta t = \omega 0,5 = \left( {2k + 1} \right)\frac{\pi }{2} \to \omega = \left( {2k + 1} \right)\pi ra{\rm{d}}/s\) \({\left( {\frac{{{u_{1N}}}}{A}} \right)^2} + {\left( {\frac{{{u_{2N}}}}{A}} \right)^2} = 1 \to A = \sqrt {{u_{1N}}^2 + {u_{2N}}^2} = \sqrt {{{\left( {6,6} \right)}^2} + {{\left( { - 3,5} \right)}^2}} = 7,5mm\)
- Tại thời điểm t1 điểm N đang đi qua vị trí cân bằng theo chiều âm do vậy tốc độ của N sẽ là:
\({v_{{N_1}}} = \omega A = 7,5\pi \left( {2k + 1} \right)mm/s\)
- Vận tốc của N tại thời điểm
\({t_0} = {t_1} - \frac{1}{9}s\) là
\({v_{{N_0}}} = - {v_{{N_1}}}{\rm{cos}}\left( {2k + 1} \right)\frac{\pi }{9}mm/s\)
Với k = 1
\( \to {v_{{N_0}}} = - 7,5\pi .3{\rm{cos}}\frac{{3\pi }}{9}mm/s = - 35,3mm/s = - 3,53cm/s\)
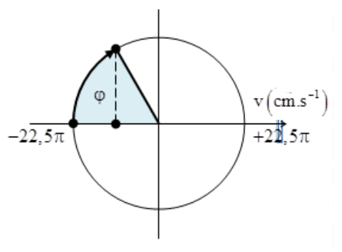
Một sợi dây đàn hồi rất dài có đầu $A$ dao động với tần số $f$ và theo phương vuông góc với sợi dây. Biên độ dao động là $4 cm$, vận tốc truyền sóng trên dây là $4 (m/s)$. Xét một điểm $M$ trên dây và cách $A$ một đoạn $28 cm$, người ta thấy M luôn luôn dao động lệch pha với $A$ một góc \(\Delta \varphi = (2k + 1)\dfrac{\pi }{2}\) với $k = 0, ±1, ±2,....$. Tính bước sóng $λ$? Biết tần số $f$ có giá trị trong khoảng từ $22 Hz$ đến $26 Hz$.
-
A.
$12 cm$
-
B.
$8 cm$
-
C.
$14 cm$
-
D.
$16 cm$
Đáp án : D
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Áp dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
Độ lệch pha:
\(\begin{array}{l}\Delta \varphi = (2k + 1)\dfrac{\pi }{2} = \dfrac{{2\pi d}}{\lambda }\\ \to f = \left( {2k + 1} \right)\dfrac{v}{{4d}}\end{array}\)
Mặt khác: $22 Hz < f < 26 Hz$
\(\begin{array}{l} \to 22 < f = \left( {2k + 1} \right)\dfrac{v}{{4d}} < 26 \\\leftrightarrow 22 < \left( {2k + 1} \right)\dfrac{4}{{4.0,28}} < 26\\ \to 2,58 < k < 3,14 \\\to k = 3\\ \to f = \left( {2.3 + 1} \right)\dfrac{4}{{4.0,28}} = 25H{\rm{z}} \\\to \lambda {\rm{ = }}\dfrac{v}{f} = \dfrac{4}{{25}} = 0,16m = 16cm\end{array}\)
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, $A$ là một điểm nút, $B$ là một điểm bụng gần $A$ nhất, $C$ là trung điểm của $AB$, với $AC = 10cm$. Biết khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại $B$ bằng biên độ dao động của phần tử tại $C$ là $0,1s$. Tốc độ truyền sóng trên dây là:
-
A.
$2 m/s$
-
B.
$0,5 m/s$
-
C.
$0,25 m/s$
-
D.
$1 m/s$
Đáp án : A
- Khoảng cách giữa trung điểm của một nút và bụng gần nhất với nút đó là: $\dfrac{\lambda }{8}$
- Khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại bụng sóng bằng biên độ dao động của phần tử tại trung điểm của bụng và nút sóng liền kề là: $\dfrac{T}{4}$
- Áp dụng công thức tính vận tốc truyền sóng: $v = \dfrac{\lambda }{T}$
Vì $B$ là điểm bụng gần nút $A$ nhất
$C$- là trung điểm của $AB$ =>
$AC = \dfrac{\lambda }{8} = 10cm \to \lambda = 80cm$
Biên độ dao động của phần tử tại $C$:
${A_C} = \sqrt 2 A$
Khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại $B$ bằng biên độ dao động của phần tử tại $C$ là:
$\dfrac{T}{4} = 0,1{\text{s}} \to T = 0,4{\text{s}}$
Vận tốc truyền sóng:
$v = \dfrac{\lambda }{T} = \dfrac{{0,8}}{{0,4}} = 2m/s$
Chọn câu sai.
-
A.
Sóng ngang có phương dao động vuông góc với phương truyền sóng.
-
B.
Sóng cơ cũng làm lan truyền vật chất trên phương truyền sóng.
-
C.
Sóng cơ truyền trong chất khí là sóng dọc.
-
D.
Bước sóng là quãng đường sóng truyền được trong thời gian bằng một chu kì sóng.
Đáp án : B
A, C, D - đúng
B - sai vì: Quá trình truyền sóng cơ là quá trình truyền các dao động, không phải là quá trình truyền các phần tử môi trường.
Chọn phát biểu sai khi nói về tốc độ truyền sóng trong một môi trường:
-
A.
Là tốc độ lan truyền dao động trong môi trường
-
B.
Phụ thuộc vào tính đàn hồi và mật độ môi trường
-
C.
Là vận tốc dao động của các phần tử vật chất khi sóng truyền qua
-
D.
\({v_R} > {v_L} > {v_K}\)
Đáp án : C
A, B, D – đúng
C – sai vì: Tốc độ truyền sóng khác vận tốc dao động của các phần tử vật chất khi sóng truyền qua.
Một sóng cơ dao động có bước sóng là \(\lambda \). Khoảng cách giữa 5 ngọn sóng liên tiếp là:
-
A.
\(5\lambda \)
-
B.
\(6\lambda \)
-
C.
\(4\lambda \)
-
D.
\(10\lambda \)
Đáp án : C
Khoảng cách giữa n ngọn sóng liên tiếp là: n - 1 bước sóng
Ta có: Khoảng cách giữa n ngọn sóng liên tiếp là: n - 1 bước sóng
=> Khoảng cách giữa 5 ngọn sóng liên tiếp là \(4\lambda \)
Một sóng hình sin đang truyền trên một sợi dây, theo chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây ở các thời điểm \({t_1}\) và \({t_2} = {\rm{ }}{t_1} + {\rm{ }}0,7s\). Chu kì của sóng là:

-
A.
0,7 s
-
B.
0,35 s
-
C.
0,8 s
-
D.
1,6 s
Đáp án : D
+ Sử dụng phương pháp đọc đồ thị dao động sóng
+ Áp dụng công thức tính vận tốc truyền sóng: \(v = \dfrac{{\Delta x}}{{\Delta t}}\)
+ Áp dụng công thức tính chu kì dao động sóng: \(T = \dfrac{\lambda }{v}\)
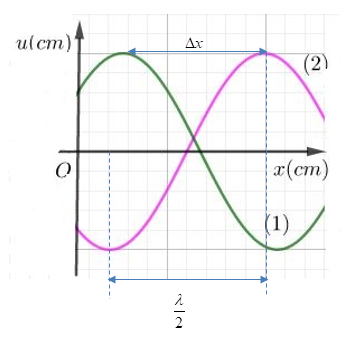
Từ đồ thị dao động sóng ta có:
+ \(\Delta x = \) 7ô
+ \(\dfrac{\lambda }{2} = \) 8ô
Vận tốc truyền sóng: \(v = \dfrac{{\Delta x}}{{\Delta t}} = \dfrac{{7{ô} }}{{0,7}}\)
Chu kì dao động sóng: \(T = \dfrac{\lambda }{v} = \dfrac{{16{ô} }}{{\dfrac{{7{ô} }}{{0,7}}}} = 1,6{\rm{s}}\)
Phát biểu nào sau đây là đúng khi nói về hiện tượng giao thoa sóng?
-
A.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau.
-
B.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
-
C.
Là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
-
D.
Là hiện tượng hai sóng khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
Đáp án : C
Hiện tượng giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.
Khi có sóng dừng trên dây, khoảng cách giữa hai bụng sóng liên tiếp bằng bao nhiêu? Biết sóng truyền trên dây có bước sóng \(\lambda = 4m\)
-
A.
\(4k\left( m \right)\) với \(k \in Z\)
-
B.
\(1\left( m \right)\)
-
C.
\(2\left( m \right)\)
-
D.
\(4\left( m \right)\)
Đáp án : C
Khoảng cách giữa 2 nút hoặc 2 bụng liền kề của sóng dừng là \(\frac{\lambda }{2} = \frac{4}{2} = 2m\)
Một sợi dây AB dài\(60{\rm{ }}cm\). Đầu A dao động với tần số \(f{\rm{ }} = {\rm{ }}50{\rm{ }}Hz\). Đầu B cố định. Trên dây AB có một sóng dừng ổn định, A được coi là nút sóng. Tốc độ truyền sóng trên dây là \(60cm/s\). Hỏi điểm M cách A một khoảng \(3cm\) là nút hay bụng thứ mấy kể từ A và trên dây có bao nhiêu nút, bao nhiêu bụng kể cả A và B.
-
A.
M là nút số 6, trên dây có 100 nút - 100 bụng.
-
B.
M là bụng số 6, trên dây có 100 nút - 100 bụng.
-
C.
M là nút số 6, trên dây có 101 nút - 100 bụng.
-
D.
M là bụng số 6, trên dây có 101 nút - 100 bụng.
Đáp án : C
+ Sử dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\)
+ Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2}{\rm{ }}(k \in {N^*})\)
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
+ Ta có, bước sóng: \(\lambda = \frac{v}{f} = \frac{{60}}{{50}} = 1,2{\rm{ }}cm\)
+ Ta có điều kiện để có sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2}{\rm{ }}(k \in {N^*})\)
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
AM = 5\(\frac{\lambda }{2}\) = 3 cm
=> M là nút số 6
\(l = k\frac{\lambda }{2}{\rm{ }} \leftrightarrow 60 = {\rm{k}}\frac{{1,2}}{2} \to k = 100\)
=> Trên dây có 100 bụng, 101 nút
Vận tốc truyền âm phụ thuộc vào các yếu tố
-
A.
Cường độ âm, độ to của âm
-
B.
Tính đàn hồi, mật độ môi trường và nhiệt độ của môi trường
-
C.
Tần số âm và nhiệt độ môi trường
-
D.
Tần số âm và cường to của âm
Đáp án : B
Ta có: Vận tốc truyền âm phụ thuộc vào tính đàn hồi, mật độ của môi trường và nhiệt độ của môi trường.
vR > vL > vK
Chọn phương án đúng trong các phương án dưới đây:
-
A.
Đối với tai con người, cường độ âm càng lớn thì âm càng nhỏ
-
B.
Cảm giác nghe cao hay thấp chỉ phụ thuộc vào cường độ âm
-
C.
Cùng một cường độ âm tai con người nghe âm cao to hơn nghe âm trầm
-
D.
Độ to là đặc trưng vật lí phụ thuộc vào tần số âm và mức cường độ âm
Đáp án : C
A – sai vì: Đối với tai con người, cường độ âm càng lớn thì âm càng to
B – sai vì: Cảm giác cao hay thấp phụ thuộc vào tần số âm
C – đúng
D – sai vì: Độ to là đặc trưng sinh lí phụ thuộc vào tần số âm và mức cường độ âm
Một dây đàn dài 12cm, khi gãy phát ra âm cơ bản với tốc độ truyền sóng trên dây là 270m/s. Tốc độ truyền âm trong không khí là 340m/s. Bước sóng của âm phát ra trong không khí là:
-
A.
0,3m
-
B.
0,076m
-
C.
0,15m
-
D.
0,6m
Đáp án : A
+ Sử dụng công thức chiều dài dây đàn: \(l = k\frac{\lambda }{2}\)
+ Sử dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\)
+ Do dây dàn (2 đầu cố định) chiều dài của dây: \(l = k\frac{\lambda }{2} = k\frac{v}{{2f}} \to f = k\frac{v}{{2l}}\)
+ Tần số của âm cơ bản (ứng với k = 1) : \({f_1} = \frac{v}{{2l}} = \frac{{270}}{{2.0,12}} = 1125H{\rm{z}}\)
+ Bước sóng của âm phát ra trong không khí: \(\lambda = \frac{{{v_{kk}}}}{{{f_1}}} = \frac{{340}}{{1125}} = 0,3m\)
Một người đứng cách một bức tường 30 m nghe một tiếng súng nổ. Vị trí đặt súng cách tường 165 m. Người và súng cùng trên đường thẳng vuông góc với tường. Sau khi nghe tiếng nổ, người này lại nghe tiếng nổ do âm thanh phản xạ trên bức tường. Tốc độ âm thanh trong không khí là 330 m/s. Khoảng thời gian giữa hai tiếng nổ là:
-
A.
\(\frac{1}{3}s\)
-
B.
\(\frac{3}{{11}}s\)
-
C.
\(\frac{1}{{11}}s\)
-
D.
\(\frac{2}{{11}}s\)
Đáp án : D
Sử dụng công thức \(S{\rm{ }} = {\rm{ }}v.t\)
Khoảng cách giữa người và súng là: L = 165 – 30 = 135 m
Gọi \({t_1}\) là thời gian lúc súng bắt đầu nổ đến tai người: \({t_1} = \frac{{{S_1}}}{v} = \frac{{135}}{v}\)
\({t_2}\) là thời gian do âm thanh phản xạ trên bức tường sau khi nghe tiếng nổ: \({t_2} = \frac{{{S_2}}}{v} = \frac{{30 + 165}}{v}\)
Thời gian giữa hai lần tiếng nổ đến tai người là: \(\Delta t = {t_2} - {t_1} = \frac{{30 + 165}}{v} - \frac{{135}}{v} = \frac{{60}}{v} = \frac{{60}}{{330}} = \frac{2}{{11}}s\)
Trên mặt nước tại hai điểm \({S_1},{\rm{ }}{S_2}\) người ta đặt hai nguồn sóng cơ kết hợp, dao động điều hoà theo phương thẳng đứng với phương trình \({u_A} = 6cos50\pi t\) và \({u_B} = 8cos50\pi t\) (\({u_A}\) và \({u_B}\) tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt nước là \(40cm/s\), coi biên độ sóng không đổi khi truyền đi. Trên đoạn thẳng \({S_1}{S_2}\), điểm dao động với biên độ \(1cm\) và cách trung điểm của đoạn \({S_1}{S_2}\) một đoạn gần nhất là:
-
A.
0,25 cm
-
B.
0,5 cm
-
C.
0,197 cm
-
D.
1 cm
Đáp án : C
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Sử dụng vòng tròn lượng giác và công thức: \(\Delta \varphi = \dfrac{{2\pi }}{\lambda }d\)
+ Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{v}{{\frac{\omega }{{2\pi }}}} = \dfrac{{40}}{{\dfrac{{50}}{{2\pi }}}} = 1,6cm\)
+ Hai nguồn cùng pha nên trung điểm I dao động cực đại: Amax = 6 + 8 = 14 mm
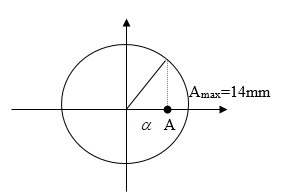
\(\cos \alpha = \dfrac{A}{{{A_{\max }}}} = \dfrac{{10}}{{14}} \\\to \alpha = 0,7751933733rad = \Delta \varphi \)
Độ lệch pha giữa I và M cần tìm là \(\Delta \varphi = \dfrac{{2\pi }}{\lambda }d = 0,77519 \to d = 0,197cm\)
Tại điểm \(O\) đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm \(A\) cách \(O\) một đoạn \(d\) (\(m\)) có mức cường độ âm là \(L_A = 40 dB\). Trên tia vuông góc với \(OA\) tại \(A\), lấy điểm \(B\) cách \(A\) một khoảng \(6 m\). Điểm \(M\) thuộc đoạn \(AB\) sao cho \(AM = 4,5 m\) và góc \(\widehat {MOB}\)có giá trị lớn nhất. Để mức cường độ âm tại \(M\) là \(50 dB\) thì cần đặt thêm tại \(O\) bao nhiêu nguồn âm nữa?
-
A.
\(35\)
-
B.
\(25\)
-
C.
\(15\)
-
D.
\(33\)
Đáp án : D
Ta sử dụng công thức:
\(\tan ({\varphi _2} - {\varphi _1}) = \dfrac{{\tan {\varphi _2} - \tan {\varphi _1}}}{{1 + \tan {\varphi _2}\tan {\varphi _1}}}\), góc MOB có giá trị lớn nhất khi tan MOB lớn nhất
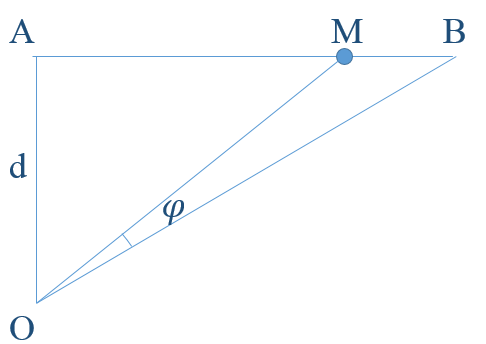
\(\tan \widehat {MOB} = \dfrac{{\tan \widehat {AOB} - \tan \widehat {AOM}}}{{1 + \tan \widehat {AOB}\tan \widehat {AOM}}} = \dfrac{{\dfrac{{AB}}{{AO}} - \dfrac{{AM}}{{AO}}}}{{1 + \dfrac{{AB}}{{AO}}.\dfrac{{AM}}{{AO}}}}\)
\( \Rightarrow \tan \varphi = \dfrac{{\dfrac{{AB}}{d} - \dfrac{{AM}}{d}}}{{1 + \dfrac{{AB}}{d}.\dfrac{{AM}}{d}}} = \dfrac{{AB - AM}}{{d + \dfrac{{AB.AM}}{d}}}\)
\( \Rightarrow \tan \varphi \) đạt cực đại khi \(\left( {d + \dfrac{{AB.AM}}{d}} \right)\) đạt min \(d = \dfrac{{AB.AM}}{d} \Leftrightarrow d = \sqrt {AB.AM} = 3\sqrt 3 (m)\)
\( \Rightarrow OM = \sqrt {A{O^2} + A{M^2}} = \dfrac{{3\sqrt {21} }}{2}(m)\)
\( \Rightarrow {L_A} - {L_M} = 20\lg \dfrac{{{r_M}}}{{{r_A}}} = 2,43(dB) \Rightarrow {L_M} = 37,57(dB)\)
Để mức cường độ âm tại M là 50 dB thì:
\({L_2} - {L_1} = 10\lg \dfrac{{{P_2}}}{{{P_1}}} = 50 - 37,57 = 12,43 \Rightarrow {P_2} \approx 35P\)
Trong đó P là công suất của một nguồn âm.
Suy ra cần thêm 33 nguồn âm nữa
Hiện tượng giao thoa ánh sáng chứng tỏ rằng ánh sáng
-
A.
là sóng ngang.
-
B.
có bản chất sóng.
-
C.
gồm các hạt phôtôn.
-
D.
là sóng dọc.
Đáp án : B
Sử dụng lí thuyết về giao thoa sóng ánh sáng
Hiện tượng giao thoa ánh sáng chứng tỏ rằng ánh sáng có bản chất sóng.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận