Đề kiểm tra 1 tiết chương 3: Dòng điện xoay chiều - Đề số 03

Làm đề thi

Đề bài

Câu 1 :

Đặt điện áp $u{\rm{ }} = {\rm{ }}{U_0}cos(\omega t)$ vào hai đầu cuộn cảm thuần có độ tự cảm L thì cường độ dòng điện qua cuộn cảm thuần là:

A.

$i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t + \dfrac{\pi }{2}} \right)$
B.

$i{\rm{ }} = {U_0}{\rm{ }}\omega Lcos\left( {\omega t + \dfrac{\pi }{2}} \right)$
C.

$i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t - \dfrac{\pi }{2}} \right)$
D.

$i{\rm{ }} = {U_0}{\rm{ }}\omega Lcos\left( {\omega t - \dfrac{\pi }{2}} \right)$

Câu 2 :

Ở máy phát điện xoay chiều một pha phần quay gọi là:

A.

Phần cảm
B.

Phần ứng
C.

Rôto
D.

Stato

Câu 3 :

Một mạch điện xoay chiều chỉ chứa cuộn cảm, $i$ là cường độ dòng điện tức thời qua mạch và $u$ là điện áp tức thời. Chọn câu đúng:

A.

i sớm pha hơn u là $\dfrac{\pi }{2}$
B.

u trễ pha hơn i là $\dfrac{\pi }{4}$
C.

u sớm pha hơn i là $\dfrac{\pi }{2}$
D.

i trễ pha hơn u là $\dfrac{\pi }{4}$

Câu 4 :

Một máy biến áp có số vòng dây cuộn sơ cấp là $2000$ vòng được mắc vào mạng điện xoay chiều có tần số $50Hz$. Cường độ dòng điện hiệu dụng cuộn sơ cấp là $2 A$ và cuộn thứ cấp là $10A$. Số vòng dây cuộn thức cấp là:

A.

10000 vòng
B.

4000 vòng
C.

400 vòng
D.

200 vòng

Câu 5 :

Một khung dây gồm N vòng dây, quay đều trong từ trường đều B với tốc độ góc $\omega $, tiết diện khung dây là S, trục quay vuông góc với đường sức từ. Suất điện động trong khung dây có giá trị hiệu dụng là:

A.

$NBS\omega \sqrt 2 $
B.

$\dfrac{1}{2}NBS\omega \sqrt 2 $
C.

$NBS\omega $
D.

$NBS/\omega $

Câu 6 :

Cho mạch điện xoay chiều RLC mắc nối tiếp. Điện áp xoay chiều đặt vào hai đầu đoạn mạch có biểu thức u= U√2cosωt tần số góc ω biến đổi. Khi ω = ω₁=40π (rad/s) và khi ω = ω₂=360π (rad/s) thì cường độ dòng điện hiệu dụng qua mạch điện có giá trị bằng nhau. Để cường độ dòng điện trong mạch đạt giá trị lớn nhất thì tần số góc ω bằng

A.

100 π (rad/s).
B.

110 π (rad/s).
C.

200 π (rad/s).
D.

120 π (rad/s)

Câu 7 :

Đặt điện áp $u = 200\sqrt 2 c{\text{os}}100\pi t(V)$ vào hai đầu một mạch điện. Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch là:

A.

$200V$
B.

$400V$
C.
$100\sqrt 2 V$
D.
$200\sqrt 2 V$

Câu 8 :

Một máy tăng áp có cuộn thứ cấp mắc với điện trở thuần, cuộn sơ cấp mắc với nguồn điện xoay chiều. Tần số dòng điện trong cuộn thứ cấp

A.

có thể nhỏ hơn hoặc lớn hơn tần số trong cuộn sơ cấp.
B.

bằng tần số dòng điện trong cuộn sơ cấp.
C.

luôn nhỏ hơn tần số dòng điện trong cuộn sơ cấp.
D.

luôn lớn hơn tần số dòng điện trong cuộn sơ cấp.

Câu 9 :

Trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Cho $L,{\rm{ }}R,\omega $ không đổi. Thay đổi C đến khi C=C₀ thì điện áp U_Lmax. Khi đó:

A.

${C_0} = \dfrac{1}{{{\omega ^2}L}}$
B.

${C_0} = \dfrac{{{R^2} + Z_C^2}}{{\omega L}}$
C.

${C_0} = \dfrac{1}{{{{(\omega L)}^2}}}\dfrac{{{R^2} + Z_C^2}}{{\omega L}}$
D.

${C_0} = \dfrac{1}{{{{(\omega L)}^2}}}$

Câu 10 :

Công suất tỏa nhiệt của dòng điện xoay chiều được tính theo công thức:

A.

$P = UI\sin \varphi $
B.

$P = UI\cos \varphi $
C.

$P = UI$
D.

$P = ui\cos \varphi $

Câu 11 :

Đoạn mạch RLC nối tiếp có hệ số công suất lớn nhất. Hệ thức nào sau đây không đúng:

A.

$P = U.I$
B.

$T = 2\pi \sqrt {L.C} $
C.

$Z = R$
D.

$U = {U_L} = {U_C}$

Câu 12 :

Trong mạch $RLC$ mắc nối tiếp, độ lệch pha giữa dòng điện và hiệu điện thế ở hai đầu đoạn mạch phụ thuộc:

A.

Cường độ dòng điện hiệu dụng trong mạch
B.

Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch
C.

Cách chọn gốc tính thời gian
D.

Tính chất của mạch điện

Câu 13 :

Trong đoạn mạch AB có ba phần tử R, L, C không phân nhánh, gọi ${u_{AB}},{\rm{ }}{u_R},{\rm{ }}{u_L},{\rm{ }}{u_C}$ lần lượt là các điện áp tức thời giữa hai đầu đoạn mạch, điện trở R, cuộn dây thuần cảm và tụ điện, i là dòng điện qua đoạn mạch. Chọn phát biểu đúng:

A.

Độ lệch pha giữa u_L và u_AB là $\frac{\pi }{2}$.
B.

u_L sớm pha hơn u_R là $\frac{\pi }{2}$
C.

u_C sớm pha hơn i là $\frac{\pi }{2}$.
D.

u_C chậm pha hơn u_AB là $\frac{\pi }{2}$.

Câu 14 :

Đặt điện áp xoay chiều có giá trị hiệu dụng $U=120V$, tần số $f=60Hz$ vào hai đầu một bóng đèn huỳnh quang. Biết đèn chỉ sáng lên khi điện áp đặt vào đèn không nhỏ hơn $60\sqrt 2 V$. Thời gian đèn sáng trong mỗi giây là:

A.

$\dfrac{1}{2}s$
B.

$\dfrac{1}{3}s$
C.

$\dfrac{2}{3}s$
D.

$\dfrac{1}{4}s$

Câu 15 :

Đoạn mạch RLC nối tiếp $R = 40\Omega $; $L = \dfrac{{0,4}}{\pi }(H)$và $C = \dfrac{{{{10}^{ - 3}}}}{\pi }(F)$. Cho tần số dòng điện là $50{\rm{ }}Hz$ và điện áp hiệu dụng ở hai đầu R là $40{\rm{ }}V$. Điện áp ở hai đầu đoạn mạch là:

A.

100 V
B.

150 V
C.

200 V
D.

50 V

Câu 16 :

Mạch điện xoay chiều chỉ chứa tụ điện $C = \frac{1}{{7200\pi }}{\rm{ }}F$ , hiệu điện thế xoay chiều ổn định đặt vào hai đầu mạch là $u = {U_0}cos\left( {\omega t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V$ . Tại thời điểm t₁ ta có ${u_1} = 60\sqrt 2 {\rm{ }}V$ và ${i_1} = \frac{{\sqrt 2 }}{2}A$ , tại thời điểm t₂ ta có ${u_2} = - {\rm{ }}60\sqrt 3 {\rm{ }}V$ và và ${i_2} = - 0,5A$ . Hãy hoàn thiện biểu thức của điện áp u.

A.

$u{\rm{ }} = 120cos\left( {100{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V$
B.

$u{\rm{ }} = 60cos\left( {120{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V$
C.

$u{\rm{ }} = 60cos\left( {50{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V$
D.

$u = 120cos\left( {60{\rm{ }}\pi {\rm{ }}t{\rm{ }} + {\rm{ }}\frac{\pi }{4}{\rm{ }}} \right){\rm{ }}V$

Câu 17 :

Đoạn mạch điện xoay chiều có điện áp ở hai đầu $u = 100\cos \left( {100\pi t + \pi /2} \right)(V)$ và dòng điện xoay chiều qua mạch $i = 2\cos \left( {100\pi t + \pi /6} \right)(A)$. Công suất tiêu thụ của mạch điện là:

A.

200 W
B.

100 W
C.

50 W
D.

86,6 W

Câu 18 :

Cho mạch điện RLC nối tiếp. Trong đó $R = 100\sqrt 3 \Omega $ , $C = \dfrac{{{{10}^{ - 4}}}}{\pi }F$ và cuộn dây thuần cảm có độ tự cảm L thay đổi được. Điện áp giữa hai đầu đoạn mạch là $u = 200cos(100\pi t){\rm{ }}V.$ Độ tự cảm của cuộn dây để điện áp hiệu dụng trên cuộn cảm L cực đại là:

A.

$L = \dfrac{{1,5}}{\pi }H$
B.

$L = \dfrac{{2,5}}{\pi }H$
C.

$L = \dfrac{3}{\pi }H$
D.

$L = \dfrac{4}{\pi }H$

Câu 19 :

Một đoạn mạch gồm tụ điện mắc nối tiếp với một cuộn dây. Điện áp giữa hai đầu cuộn dây lệch pha $\dfrac{\pi }{3}$ so với cường độ dòng điện và lệch pha $\dfrac{\pi }{2}$ so với điện áp hai đầu đoạn mạch. Biết điện áp hiệu dụng giữa hai đầu đoạn mạch bằng $100V$, khi đó điện áp hiệu dụng trên tụ điện và trên cuộn dây lần lượt là:

A.

$60V$ và $60\sqrt 3 V$
B.

$200V$ và $100\sqrt 3 V$
C.

$60\sqrt 3 V$ và $100V$
D.

$100\sqrt 3 V$ và $200V$

Câu 20 :

Đặt một điện áp xoay chiều $u = 60\sin \left( {100\pi t} \right)V$ vào hai đầu đoạn mạch gồm cuộn thuần cảm có hệ số tự cảm $L = \dfrac{1}{\pi }H$ và tụ điện có điện dung $C = \dfrac{{50}}{\pi }\mu F$ mắc nối tiếp. Biểu thức của cường độ dòng điện chạy trong mạch là:

A.

$i = 0,2\sin \left( {100\pi t + \dfrac{\pi }{2}} \right)A$
B.

$i = 0,2\sin \left( {100\pi t - \dfrac{\pi }{2}} \right)A$
C.

$i = 0,6\sin \left( {100\pi t + \dfrac{\pi }{2}} \right)A$
D.

$i = 0,6\sin \left( {100\pi t - \dfrac{\pi }{2}} \right)A$

Câu 21 :

Mạch X có hai phần tử, u nhanh pha hơn $i$, Ghép X với Y thì thấy trong mạch có biểu thức $i = \dfrac{u}{Z}$. Hãy xác định phần tử có thể có của Y?

A.

C
B.

R, C
C.

R, L
D.

A, B đúng

Câu 22 :

Một máy phát điện xoay chiều với một khung dây có 1000 vòng, quay đều trong từ trường đều có B = 0,11T, diện tích mỗi vòng dây là 90cm², suất điện động cảm ứng trong khung có giá trị hiệu dụng là 220V. Chu kì của suất điện động là:

A.

0,02s
B.

0,028s
C.

0,014s
D.

0,01s

Câu 23 :

Hiệu điện thế do nhà máy phát ra $10 kV$. Nếu truyền tải ngay hao phí truyền tải sẽ là $5kW$. Nhưng nếu trước khi truyền tải hiệu điện thế được nâng lên $40kV$ thì hao phí trên đường truyền tải là bao nhiêu?

A.

$1,25 kW$
B.

$0,3125 kW$
C.

$25 kW$
D.

$1 kW$

Câu 24 :

Lần lượt mắc một điện trở $R$, một cuộn dây, một tụ điện $C$ vào cùng một nguồn điện ổn định và đo cường đọ dòng điện qua chúng thì được các giá trị ( theo thứ tự ) là $1A,{\rm{ }}1A$, và $0A$; điện năng tiêu thụ trên $R$ trong thời gian $\Delta t$ khi đó là $Q$. Sau đó mắc nối tiếp các linh kiện trên cùng với một ampe kế nhiệt lí tưởng vào một nguồn ổn định thứ hai thì số chỉ ampe kế là $1A$. Biết nếu xét trong cùng thời gian $\Delta t$ thì: điện năng tiêu thụ trên $R$ khi chỉ mắc nó vào nguồn thứ hai là $4Q$; còn khi mắc cuộn dây vào nguồn này thì điện năng tiêu thụ trong thời gian này cũng là $Q$. Hỏi nếu mắc điện trở $R$ nối tiếp với tụ và ampe kế nhiệt vào nguồn thứ hai thì ampe kế chỉ bao nhiêu?

A.

$1A$
B.

$2A$
C.

$\sqrt 2 A$
D.

$0,5A$

Câu 25 :

Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi $u = 120\sqrt 2 {\rm{cos100}}\pi {\rm{t}}\left( V \right)$ vào đoạn mạch $AB$ gồm đoạn $AM$chỉ chứa điện trở $R$, đoạn mạch $MB$ chứa tụ điện có điện dung $C$ thay đổi được mắc nối tiếp với một cuộn cảm thuần. Biết sau khi thay đổi $C$ thì điện áp hiệu dụng hai đầu mạch $MB$ tăng $\sqrt 2 $ lần và dòng điện tức thời trong mạch trước và sau khi thay đổi $C$ lệch pha nhau một góc $\dfrac{{5\pi }}{{12}}$. Điện áp hiệu dụng hai đầu mạch $AM$ khi chưa thay đổi $C$ có giá trị bằng:

A.

$60\sqrt 3 V$
B.

$60\sqrt 2 V$
C.

$120{\rm{ }}V$
D.

$60{\rm{ }}V$

Lời giải và đáp án

Câu 1 :

Đặt điện áp $u{\rm{ }} = {\rm{ }}{U_0}cos(\omega t)$ vào hai đầu cuộn cảm thuần có độ tự cảm L thì cường độ dòng điện qua cuộn cảm thuần là:

A.

$i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t + \dfrac{\pi }{2}} \right)$
B.

$i{\rm{ }} = {U_0}{\rm{ }}\omega Lcos\left( {\omega t + \dfrac{\pi }{2}} \right)$
C.

$i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t - \dfrac{\pi }{2}} \right)$
D.

$i{\rm{ }} = {U_0}{\rm{ }}\omega Lcos\left( {\omega t - \dfrac{\pi }{2}} \right)$

Đáp án : C

Lời giải chi tiết :

Ta có:

+ u_L nhanh pha hơn i một góc $\dfrac{\pi }{2}$

+ Cường độ dòng điện cực đại:

${I_0} = \dfrac{{{U_0}}}{{{Z_L}}} = \dfrac{{{U_0}}}{{\omega L}}$

=> Biểu thức cường độ dòng điện qua cuộn cảm thuần là:

$i{\rm{ }} = {\rm{ }}\dfrac{{{U_0}}}{{\omega L}}cos\left( {\omega t - \dfrac{\pi }{2}} \right)$

Câu 2 :

Ở máy phát điện xoay chiều một pha phần quay gọi là:

A.

Phần cảm
B.

Phần ứng
C.

Rôto
D.

Stato

Đáp án : C

Phương pháp giải :

Xem lí thuyết phần 1

Lời giải chi tiết :

Ở máy phát điện xoay chiều một pha phần quay gọi là rôto

Câu 3 :

Một mạch điện xoay chiều chỉ chứa cuộn cảm, $i$ là cường độ dòng điện tức thời qua mạch và $u$ là điện áp tức thời. Chọn câu đúng:

A.

i sớm pha hơn u là $\dfrac{\pi }{2}$
B.

u trễ pha hơn i là $\dfrac{\pi }{4}$
C.

u sớm pha hơn i là $\dfrac{\pi }{2}$
D.

i trễ pha hơn u là $\dfrac{\pi }{4}$

Đáp án : C

Lời giải chi tiết :

Trong mạch xoay chiều chỉ có cuộn cảm thì điện áp nhanh pha hơn dòng điện góc π/2:

$\varphi $_u = $\varphi $_i + π/2

Câu 4 :

A.

10000 vòng
B.

4000 vòng
C.

400 vòng
D.

200 vòng

Đáp án : C

Phương pháp giải :

Vận dụng biểu thức: $\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}} = \dfrac{{{I_2}}}{{{I_1}}}$

Lời giải chi tiết :

Ta có:

$\dfrac{{{I_2}}}{{{I_1}}} = \dfrac{{{N_1}}}{{{N_2}}} \leftrightarrow \dfrac{{10}}{2} = \dfrac{{2000}}{{{N_2}}} = 10 \to {N_2} = 400$

=> Số vòng dây ở cuộn thứ cấp là 400 vòng

Câu 5 :

A.

$NBS\omega \sqrt 2 $
B.

$\dfrac{1}{2}NBS\omega \sqrt 2 $
C.

$NBS\omega $
D.

$NBS/\omega $

Đáp án : B

Lời giải chi tiết :

Suất điện động trong khung dây có giá trị cực đại là: E₀ = ωNBS

=> Giá trị hiệu dụng của suất điện động trong khung dây là: $E = \dfrac{{{E_0}}}{{\sqrt 2 }} = \dfrac{{NBS\omega }}{{\sqrt 2 }}$

Câu 6 :

A.

100 π (rad/s).
B.

110 π (rad/s).
C.

200 π (rad/s).
D.

120 π (rad/s)

Đáp án : D

Lời giải chi tiết :

$\omega = \sqrt {{\omega _1}{\omega _2}} = 120\pi \left( {rad/s} \right)$

Câu 7 :

Đặt điện áp $u = 200\sqrt 2 c{\text{os}}100\pi t(V)$ vào hai đầu một mạch điện. Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch là:

A.

$200V$
B.

$400V$
C.
$100\sqrt 2 V$
D.
$200\sqrt 2 V$

Đáp án : A

Phương pháp giải :

+ Đọc phương trình điện áp

+ Sử dụng biểu thức tính hiệu điện thế hiệu dụng $U = \dfrac{{{U_0}}}{{\sqrt 2 }}$

Lời giải chi tiết :

Hiệu điện thế hiệu dụng: $U = \dfrac{{200\sqrt 2 }}{{\sqrt 2 }} = 200V$

Câu 8 :

Một máy tăng áp có cuộn thứ cấp mắc với điện trở thuần, cuộn sơ cấp mắc với nguồn điện xoay chiều. Tần số dòng điện trong cuộn thứ cấp

A.

có thể nhỏ hơn hoặc lớn hơn tần số trong cuộn sơ cấp.
B.

bằng tần số dòng điện trong cuộn sơ cấp.
C.

luôn nhỏ hơn tần số dòng điện trong cuộn sơ cấp.
D.

luôn lớn hơn tần số dòng điện trong cuộn sơ cấp.

Đáp án : B

Lời giải chi tiết :

Máy biến thế là những thiết bị có khả năng biến đổi điện áp (xoay chiều) và không làm thay đổi tần số của nó.

Câu 9 :

Trong mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Cho $L,{\rm{ }}R,\omega $ không đổi. Thay đổi C đến khi C=C₀ thì điện áp U_Lmax. Khi đó:

A.

${C_0} = \dfrac{1}{{{\omega ^2}L}}$
B.

${C_0} = \dfrac{{{R^2} + Z_C^2}}{{\omega L}}$
C.

${C_0} = \dfrac{1}{{{{(\omega L)}^2}}}\dfrac{{{R^2} + Z_C^2}}{{\omega L}}$
D.

${C_0} = \dfrac{1}{{{{(\omega L)}^2}}}$

Đáp án : A

Lời giải chi tiết :

Ta có: C biến thiên để U_L max <=> mạch xảy ra hiện tượng cộng hưởng điện

$\begin{array}{l} \leftrightarrow {Z_C} = {Z_L} \leftrightarrow \frac{1}{{\omega {C_0}}} = \omega L\\ \to {C_0} = \frac{1}{{{\omega ^2}L}}\end{array}$

Câu 10 :

Công suất tỏa nhiệt của dòng điện xoay chiều được tính theo công thức:

A.

$P = UI\sin \varphi $
B.

$P = UI\cos \varphi $
C.

$P = UI$
D.

$P = ui\cos \varphi $

Đáp án : B

Lời giải chi tiết :

Công suất của dòng điện xoay chiều được tính theo công thức:

$P = UI\cos \varphi $

Câu 11 :

Đoạn mạch RLC nối tiếp có hệ số công suất lớn nhất. Hệ thức nào sau đây không đúng:

A.

$P = U.I$
B.

$T = 2\pi \sqrt {L.C} $
C.

$Z = R$
D.

$U = {U_L} = {U_C}$

Đáp án : D

Lời giải chi tiết :

Ta có, mạch RLC mắc nối tiếp có hệ số công suất lớn nhất khi:

${Z_L} = {Z_C}$

Khi đó, ta có:

+ $\omega = \frac{1}{{\sqrt {LC} }} \to T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {LC} $

+ Công suất cực đại:

${P_{{\rm{max}}}} = UI$

+ Tổng trở khi đó:

$Z = R$

+ $U = {U_R}$

=> Phương án D - sai

Câu 12 :

Trong mạch $RLC$ mắc nối tiếp, độ lệch pha giữa dòng điện và hiệu điện thế ở hai đầu đoạn mạch phụ thuộc:

A.

Cường độ dòng điện hiệu dụng trong mạch
B.

Hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch
C.

Cách chọn gốc tính thời gian
D.

Tính chất của mạch điện

Đáp án : D

Phương pháp giải :

Sử dụng biểu thức tính độ lệch pha giữa điện áp và dòng điện trong mạch điện xoay chiều: $\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}$

Lời giải chi tiết :

+ Độ lệch pha $\varphi $ giữa $u$ và $v$ được tính bởi công thức: $\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}$

+ Vì điện trở: $R > 0 \to \tan \varphi $ phụ thuộc vào ${Z_L}$ và ${Z_C}$ => Phụ thuộc vào tính chất của mạch điện (mạch có tính dung kháng hay cảm kháng)

Câu 13 :

A.

Độ lệch pha giữa u_L và u_AB là $\frac{\pi }{2}$.
B.

u_L sớm pha hơn u_R là $\frac{\pi }{2}$
C.

u_C sớm pha hơn i là $\frac{\pi }{2}$.
D.

u_C chậm pha hơn u_AB là $\frac{\pi }{2}$.

Đáp án : B

Lời giải chi tiết :

A, C, D - sai

B - đúng

Câu 14 :

A.

$\dfrac{1}{2}s$
B.

$\dfrac{1}{3}s$
C.

$\dfrac{2}{3}s$
D.

$\dfrac{1}{4}s$

Đáp án : C

Phương pháp giải :

+ Sử dụng vòng tròn lượng giác

+ Vận dụng biểu thức tính tần số góc: $\omega = 2\pi f$

+ Vận dụng biểu thức: $\Delta \varphi = \omega \Delta t$

Lời giải chi tiết :

Ta có:

+ Hiệu điện thế cực đại:

${U_0} = 120\sqrt 2 (V)$

+ Tần số góc:

$\omega = 2\pi f = 2\pi .60 = 120\pi (ra{\text{d}}/s)$

+ Vẽ trên vòng tròn lượng giác, ta được:

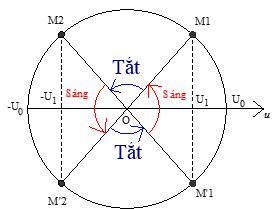
Biết đèn chỉ sáng lên khi u ≥ U₁

Ta có:

+ $c{\text{os}}\Delta \varphi = \dfrac{{{U_1}}}{{{U_0}}} = \dfrac{{60\sqrt 2 }}{{120\sqrt 2 }} = 0,5 \to \Delta \varphi = \dfrac{\pi }{3}$

Thời gian đèn sáng trong 1 chu kì:

$\Delta t = \dfrac{{4\Delta \varphi }}{\omega } = \dfrac{{4\dfrac{\pi }{3}}}{{120\pi }} = \dfrac{1}{{90}}s$

Ta có:

+ Chu kì: $T = \dfrac{1}{f} = \dfrac{1}{{60}}s$

+ $1{\text{s}} = 60T$

=> Thời gian đèn sáng trong 1s là:

$t = \Delta t.60 = 60.\dfrac{1}{{90}} = \dfrac{2}{3}s$

Câu 15 :

A.

100 V
B.

150 V
C.

200 V
D.

50 V

Đáp án : D

Phương pháp giải :

+ Vận dụng biêu thức tính hiệu điện thế: $U = I.Z$

+ Vận dụng biểu thức tính cảm kháng, dung kháng: ${Z_L} = \omega L;{Z_C} = \dfrac{1}{{\omega C}}$

+ Vận dụng biểu thức tính hiệu điện thế hiệu dụng toàn mạch: $U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} $

Lời giải chi tiết :

Ta có:

Cường độ dòng điện trong mạch: $I = \dfrac{{{U_R}}}{R} = \dfrac{{40}}{{40}} = 1(A)$

Cảm kháng: ${Z_L} = \omega L = 2\pi fL = 2\pi .50.\dfrac{{0,4}}{\pi } = 40\Omega $

Hiệu điện thế hiệu dụng hai đầu cuộn cảm: ${U_L} = I.{Z_L} = 1.40 = 40(V)$

Dung kháng: ${Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 3}}}}{\pi }}} = 10\Omega $

Hiệu điện thế hiệu dụng hai đầu tụ điện: ${U_C} = I.{Z_C} = 1.10 = 10(V)$

Hiệu điện thế hiệu dụng toàn mạch: $U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = \sqrt {{{40}^2} + {{\left( {40 - 10} \right)}^2}} = 50(V)$

Câu 16 :

A.

$u{\rm{ }} = 120cos\left( {100{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V$
B.

$u{\rm{ }} = 60cos\left( {120{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V$
C.

$u{\rm{ }} = 60cos\left( {50{\rm{ }}\pi {\rm{ }}t{\rm{ }} + \frac{\pi }{4}} \right){\rm{ }}V$
D.

$u = 120cos\left( {60{\rm{ }}\pi {\rm{ }}t{\rm{ }} + {\rm{ }}\frac{\pi }{4}{\rm{ }}} \right){\rm{ }}V$

Đáp án : D

Phương pháp giải :

Vận dụng biểu thức: $\frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1$

Lời giải chi tiết :

Do mạch chỉ có C nên: $u \bot i \to \frac{{{u^2}}}{{U_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1$

Thay các giá trị, ta có:

$\begin{array}{l}\left\{ \begin{array}{l}\frac{{{{(60\sqrt 2 )}^2}}}{{U_0^2}} + \frac{{{{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2}}}{{I_0^2}} = 1{\rm{ (1)}}\\\frac{{{{\left( {60\sqrt 3 } \right)}^2}}}{{U_0^2}} + \frac{{{{\left( {0,5} \right)}^2}}}{{I_0^2}} = 1{\rm{ (2)}}\end{array} \right.\\ \to \frac{{3600}}{{U_0^2}} = \frac{{0,25}}{{I_0^2}} \to \frac{{{U_0}}}{{{I_0}}} = 120 = {Z_C}\end{array}$

Lại có, ${Z_C} = \frac{1}{{\omega C}} \to \omega = \frac{1}{{{Z_C}C}} = \frac{1}{{120.C}} = \frac{1}{{120.\frac{1}{{7200\pi }}}} = 60\pi $

Thay ${I_0} = \frac{{{U_0}}}{{120}}$ vào (1) , ta được: $\frac{{{{(60\sqrt 2 )}^2}}}{{U_0^2}} + \frac{{{{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2}}}{{\frac{{U_0^2}}{{{{120}^2}}}}} = 1 \to {U_0} = 120(V)$

$ \to u = 120cos\left( {60{\rm{ }}\pi {\rm{ }}t{\rm{ }} + {\rm{ }}\frac{\pi }{4}{\rm{ }}} \right){\rm{ }}V$

Câu 17 :

A.

200 W
B.

100 W
C.

50 W
D.

86,6 W

Đáp án : C

Phương pháp giải :

Áp dụng biểu thức xác định công suất tiêu thụ của mạch điện: $P = UIcos\varphi $

Lời giải chi tiết :

Ta có:

+ Độ lệch pha giữa u và i:

$\varphi = \dfrac{\pi }{2} - \dfrac{\pi }{6} = \dfrac{\pi }{3}(ra{\rm{d}})$

+ Công suất tiêu thụ của mạch điện:

$P = UIcos\varphi = \dfrac{{100}}{{\sqrt 2 }}.\dfrac{2}{{\sqrt 2 }}.c{\rm{os}}\dfrac{\pi }{3} = 50{\rm{W}}$

Câu 18 :

A.

$L = \dfrac{{1,5}}{\pi }H$
B.

$L = \dfrac{{2,5}}{\pi }H$
C.

$L = \dfrac{3}{\pi }H$
D.

$L = \dfrac{4}{\pi }H$

Đáp án : D

Lời giải chi tiết :

Ta có: ${Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega $

L biến thiên để U_L max khi đó: ${Z_L} = \dfrac{{{R^2} + Z_C^2}}{{{Z_C}}}$

$ \to {Z_L} = \dfrac{{{{(100\sqrt 3 )}^2} + {{100}^2}}}{{100}} = 400\Omega $

Mặt khác: ${Z_L} = \omega L \to L = \dfrac{{{Z_L}}}{\omega } = \dfrac{{400}}{{100\pi }} = \dfrac{4}{\pi }(H)$

Câu 19 :

A.

$60V$ và $60\sqrt 3 V$
B.

$200V$ và $100\sqrt 3 V$
C.

$60\sqrt 3 V$ và $100V$
D.

$100\sqrt 3 V$ và $200V$

Đáp án : B

Phương pháp giải :

Sử dụng giản đồ véc-tơ và các hệ thức trong tam giác

Lời giải chi tiết :

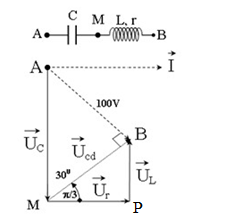
Từ giản đồ, ta có:

+ Xét $\Delta AMB$ vuông tại B, có:

$\begin{array}{l}\tan {30^0} = \dfrac{{AB}}{{MB}} = \dfrac{U}{{{U_{cd}}}}\\ \Rightarrow {U_{cd}} = \dfrac{U}{{\tan {{30}^0}}} = \dfrac{{100}}{{\dfrac{1}{{\sqrt 3 }}}} = 100\sqrt 3 V\end{array}$

$\begin{array}{l}\sin {30^0} = \dfrac{{AB}}{{AM}} = \dfrac{U}{{{U_C}}}\\ \Rightarrow {U_C} = \dfrac{U}{{\sin {{30}^0}}} = \dfrac{{100}}{{\dfrac{1}{2}}} = 200V\end{array}$

Câu 20 :

A.

$i = 0,2\sin \left( {100\pi t + \dfrac{\pi }{2}} \right)A$
B.

$i = 0,2\sin \left( {100\pi t - \dfrac{\pi }{2}} \right)A$
C.

$i = 0,6\sin \left( {100\pi t + \dfrac{\pi }{2}} \right)A$
D.

$i = 0,6\sin \left( {100\pi t - \dfrac{\pi }{2}} \right)A$

Đáp án : C

Phương pháp giải :

Sử dụng máy tính casio

Lời giải chi tiết :

Cài đặt máy tính ở chế độ radian SHIFT MODE 4

Bấm máy tính MODE 2 (Chọn CMPLX)

Cảm kháng của cuộn dây Z_L = ωL = 100 Ω

Dung kháng của tụ điện Z_C = 1/ωC = 200 Ω

Tổng trở của đoạn mạch là $\overline Z = \left( {{Z_L} - {Z_C}} \right)i = (100-200)i= - 100i$

Cường độ dòng điện trong mạch là $\overline I = \dfrac{{\overline U }}{{\overline Z }} = \dfrac{{60\angle 0}}{{ - 100i}}$ SHIFT 2 3 =

Ta đọc kết quả $\overline I = \dfrac{3}{5}\angle \dfrac{\pi }{2}$

Biểu thức cường độ dòng điện trong mạch $i = 0,6\sin \left( {100\pi t + \dfrac{\pi }{2}} \right)A$

Câu 21 :

Mạch X có hai phần tử, u nhanh pha hơn $i$, Ghép X với Y thì thấy trong mạch có biểu thức $i = \dfrac{u}{Z}$. Hãy xác định phần tử có thể có của Y?

A.

C
B.

R, C
C.

R, L
D.

A, B đúng

Đáp án : D

Phương pháp giải :

Vận dụng các phương pháp giải bài toán hộp đen (Xem lí thuyết phần 1)

Lời giải chi tiết :

Do u nhanh pha hơn i nên trong mạch X có R,L .

Mặt khác, khi nối tiếp với đoạn mạch Y thì $i = \dfrac{u}{Z}$

=> i cùng pha vơi u

=> Trong mạch xảy ra hiện tượng cộng hưởng

=> Trong mạch Y có thể chứa phần tử C sao cho $Z_L=Z_C$ hoặc chứa R, C sao cho $Z_L=Z_C$

$\to$ Phương án A, B đúng

Câu 22 :

A.

0,02s
B.

0,028s
C.

0,014s
D.

0,01s

Đáp án : A

Phương pháp giải :

+ Vận dụng biểu thức tính biên độ suất điện động: ${E_0} = \omega NBS = \omega N{\Phi _0}$

+ Vận dụng biêu thức tính chu kì: $T = \frac{{2\pi }}{\omega }$

Lời giải chi tiết :

Ta có:

+ Biên độ suất điện động:

${E_0} = \omega NBS \to \omega = \frac{{{E_0}}}{{NBS}} = \frac{{E\sqrt 2 }}{{NBS}} = \frac{{220\sqrt 2 }}{{1000.0,11.({{90.10}^{ - 4}})}} = 314,27(ra{\rm{d}}/s)$

+ Chu kì : $T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{314,27}} = 0,01999 \approx 0,02{\rm{s}}$

Câu 23 :

A.

$1,25 kW$
B.

$0,3125 kW$
C.

$25 kW$
D.

$1 kW$

Đáp án : B

Phương pháp giải :

Áp dụng công thức hao phí: $\Delta P = \dfrac{{{P^2}R}}{{{U^2}co{s^2}\varphi }}$

Lời giải chi tiết :

+ Khi $U = 10kV$ thì $\Delta P = \dfrac{{{P^2}R}}{{{U^2}co{s^2}\varphi }}$

+ Khi $U' = 40kV$ thì $\Delta P' = \dfrac{{{P^2}R}}{{U{'^2}co{s^2}\varphi }}$

$\begin{array}{l} \Rightarrow \dfrac{{\Delta P}}{{\Delta P'}} = \dfrac{{U{'^2}}}{{{U^2}}} = \dfrac{{{{\left( {{{40.10}^3}} \right)}^2}}}{{{{\left( {{{10.10}^3}} \right)}^2}}} = 16\\ \Rightarrow \Delta P' = \dfrac{{\Delta P}}{{16}} = \dfrac{5}{{16}}kW = 0,3125kW\end{array}$

Câu 24 :

A.

$1A$
B.

$2A$
C.

$\sqrt 2 A$
D.

$0,5A$

Đáp án : A

Phương pháp giải :

Sử dụng công thức tính điện năng tiêu thụ: $Q = {I^2}Rt$

Lời giải chi tiết :

+ Ban đầu cường độ dòng điện qua R. cuộn dây và C lần lượt là $1A,1A,0A$, chứng tỏ dòng điện ban đầu là dòng điện không đổi, và cuộn dây có điện trở thuần bằng R sau đó dùng dòng điện xoay chiều.

Điện năng tiêu thụ ban đầu là : $Q = \frac{{{U^2}}}{R}.\Delta t$

Điện năng tiêu thụ khi đặt vào dòng điện lúc sau và chỉ có R là: $Q' = \frac{{{U^2}}}{R}\Delta t = 4Q = 4.\frac{{{U^2}}}{R}{\rm{ }} = > U' = 2U{\rm{ }}$

+ Khi cho dòng điện qua cuộn dây ta có:

$\begin{array}{l}Q'' = \frac{{U{'^2}}}{{{{(R)}^2} + Z_L^2}}R.\Delta t = Q = \frac{{{U^2}}}{R}\Delta t\\ \leftrightarrow \frac{{4{U^2}}}{{{R^2} + Z_L^2}} = \frac{{{U^2}}}{R} \to {Z_L} = \sqrt 3 .R\end{array}$

Khi mắc cả ba linh kiện vào dòng điện thừ 2 thì cường độ dòng điện là $1A$.

Ta có: $\frac{{U'}}{{\sqrt {{{\left( {2R} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{U}{R}{\rm{ }} = > {Z_C} = {Z_L} = \sqrt 3 R{\rm{ }}$

Khi mắc điện trở với tụ vào mạch thứ hai thì cường độ dòng điện là: $I = \frac{{U'}}{{\sqrt {{R^2} + Z_C^2} }} = \frac{{2U}}{{2R}} = 1A$

Câu 25 :

A.

$60\sqrt 3 V$
B.

$60\sqrt 2 V$
C.

$120{\rm{ }}V$
D.

$60{\rm{ }}V$

Đáp án : A

Phương pháp giải :

+ Vận dụng biểu thức tính độ lệch pha của i so với u

+ Vận dụng các công thức lượng giác

+ Vận dụng máy tính giải phương trình

Lời giải chi tiết :

Ta có ${\varphi _{i1}} - {\varphi _{12}} = \left( {{\varphi _u} - {\varphi _1}} \right) - \left( {{\varphi _u} - {\varphi _2}} \right) = {\varphi _2} - {\varphi _1} = \dfrac{{5\pi }}{{12}}\left( 1 \right)$

(Giả sử trường hợp một mạch có tính dung kháng và trường hợp hai mạch có tính cảm kháng).

*Trước và sau khi thay đổi C ta có hai trường hợp, trong đó một trường hợp mạch có tính cảm kháng và một trường hợp mạch có tính dung kháng $\left\{ \begin{array}{l}\sin {\varphi _1} = \dfrac{{{U_{1LC}}}}{U}\\\sin {\varphi _2} = \dfrac{{{U_{2LC}}}}{U}\end{array} \right. = > \left\{ \begin{array}{l}{\varphi _1} = - \arcsin \dfrac{{{U_{1LC}}}}{U} = - \arcsin \dfrac{{{U_{1LC}}}}{{120}}\\{\varphi _2} = \arcsin \dfrac{{{U_{2LC}}}}{U} = \arcsin \dfrac{{\sqrt 2 {U_{1LC}}}}{{120}}\end{array} \right.$

Thế vào (1), ta được:

$\begin{array}{l}\arcsin \dfrac{{\sqrt 2 {U_{1LC}}}}{{120}} + \arcsin \dfrac{{{U_{1LC}}}}{{120}} = \dfrac{{5\pi }}{{12}} \Rightarrow {U_{1LC}} = 60V\\ \Rightarrow {U_{1R}} = \sqrt {{U^2} - U_{1LC}^2} = \sqrt {{{120}^2} + {{60}^2}} = 60\sqrt 3 V\end{array}$

Đề kiểm tra 1 tiết chương 4: Dao động và sóng điện từ - Đề số 1

Xem chi tiết

Đề kiểm tra 1 tiết chương 5: Sóng ánh sáng - Đề số 1

Xem chi tiết

Đề kiểm tra 1 tiết chương 5: Sóng ánh sáng - Đề số 2

Xem chi tiết

Đề kiểm tra 1 tiết chương 5: Sóng ánh sáng - Đề số 3

Xem chi tiết

Đề kiểm tra 1 tiết chương 6: Lượng tử ánh sáng - Đề số 1

Xem chi tiết

Đề kiểm tra 1 tiết chương 6: Lượng tử ánh sáng - Đề số 2

Xem chi tiết

Đề kiểm tra 1 tiết chương 6: Lượng tử ánh sáng - Đề số 3

Xem chi tiết

Đề kiểm tra 1 tiết chương 7: Hạt nhân nguyên tử - Đề số 2

Xem chi tiết

Đề kiểm tra 1 tiết chương 7: Hạt nhân nguyên tử - Đề số 3

Xem chi tiết

Đề kiểm tra 1 tiết chương 7: Hạt nhân nguyên tử - Đề số 1

Xem chi tiết

Đề kiểm tra 1 tiết chương 3: Dòng điện xoay chiều - Đề số 02

Xem chi tiết

Đề kiểm tra 1 tiết chương 3: Dòng điện xoay chiều - Đề số 01

Xem chi tiết

Đề kiểm tra 1 tiết chương 2: Sóng cơ và sóng âm - Đề số 03

Xem chi tiết

Đề kiểm tra 1 tiết chương 2: Sóng cơ và sóng âm - Đề số 02

Xem chi tiết

Đề kiểm tra 1 tiết chương 2: Sóng cơ và sóng âm - Đề số 01

Xem chi tiết

Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 03

Xem chi tiết

Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 02

Xem chi tiết

Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 01

Xem chi tiết

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục

Đề kiểm tra 1 tiết chương 3: Dòng điện xoay chiều - Đề số 03

Bài giải mới nhất

Báo lỗi góp ý