Đề kiểm tra 1 tiết chương 1: Dao động cơ - Đề số 02
Đề bài
Phát biểu nào sau đây là đúng khi nói về dao động tắt dần?
-
A.
Cơ năng của vật dao động tắt dần giảm dần theo thời gian.
-
B.
Biên độ của vật dao động tắt dần không đổi theo thời gian.
-
C.
Lực cản môi trường tác dụng lên vật luôn sinh công dương.
-
D.
Dao động tắt dần là dao động chỉ chịu tác dụng của nội lực.
Phát biểu nào sau đây là đúng khi nói về độ lệch pha giữa hai dao động:
-
A.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \): hai dao động ngược pha
-
B.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \): hai dao động cùng pha
-
C.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \) : hai dao động vuông pha
-
D.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \) : Biên độ tổng hợp A = A1+A2
Phương trình dao động điều hòa của một chất điểm có dạng \(x = {\rm{ }}Acos\left( a \right)t\) .Độ dài quỹ đạo của dao động là:
-
A.
A
-
B.
2A
-
C.
4A
-
D.
A/2
Khi nói về một vật dao động điều hòa có biên độ $A$ và chu kì $T$, với mốc thời gian $(t = 0)$ là lúc vật ở vị trí biên, phát biểu nào sau đây là sai?
-
A.
Sau thời gian $T/8$, vật đi được quãng đường bằng $0,5A$
-
B.
Sau thời gian $T/2$, vật đi được quãng đường bằng $2A$
-
C.
Sau thời gian $T/4$, vật đi được quãng đường bằng $A$
-
D.
Sau thời gian $T$, vật đi được quãng đường bằng $4A$
Lấy g = π2 = 10 m/s2. Treo con lắc đơn có độ dài ℓ = 100 cm trong thang máy, cho thang máy chuyển động nhanh dần đều đi lên với gia tốc a = 2 m/s2 thì chu kì dao động của con lắc đơn là:
-
A.
Tăng 11,8%.
-
B.
Giảm 16,67%.
-
C.
Giảm 8,7 %.
-
D.
Tăng 25%.
Cho một chất điểm dao động điều hòa với tần số $1Hz$, thời điểm đầu vật qua vị trí $x = 5cm$ theo chiều dương với tốc độ \(v = 10\pi cm/s\). Viết phương trình dao động.
-
A.
\(x{\text{ }} = {\text{ }}5\sqrt 2 sin(2\pi t{\text{ }} + \frac{\pi }{4}){\text{ }}cm\)
-
B.
\(x = 5\cos (2\pi t - \frac{\pi }{6})cm\)
-
C.
\(x{\text{ }} = {\text{ }}5sin(2\pi t{\text{ }} + \frac{\pi }{4}){\text{ }}cm\)
-
D.
\(x{\text{ }} = {\text{ }}5\sqrt 2 sin(2\pi t{\text{ }} - \frac{\pi }{6}){\text{ }}cm\)
Một con lắc đơn đang dao động điều hòa với biên độ góc α0 tại nơi có gia tốc trọng trường là g. Biết lực căng dây lớn nhất bằng 1.02 lần lực căng dây nhỏ nhất. Giá trị của α0 là ?
-
A.
3,30
-
B.
6,60
-
C.
5,60
-
D.
9,60
Một vật dao động điều hòa với phương trình: \(x = 10c{\rm{os}}\left( {20\pi t - \dfrac{\pi }{6}} \right)cm\). Xác định thời điểm thứ $2016$ vật có gia tốc bằng không?
-
A.
$100,767s$
-
B.
$100,783s$
-
C.
$100,8s$
-
D.
$100,733s$
Một lò xo có độ cứng \(k = 25(N/m)\). Một đầu của lò xo gắn vào điểm O cố định. Treo vào lò xo hai vật có khối lượng \(m = 100g\) và \(∆m = 60g\). Tính độ dãn của lò xo khi vật cân bằng và tần số góc dao động của con lắc.
-
A.
\(\Delta {l_0} = 4,4\left( {cm} \right);\omega = 12,5\left( {rad/s} \right)\)
-
B.
\(\Delta {l_0} = 6,4\left( {cm} \right);\omega = 12,5\left( {rad/s} \right)\)
-
C.
\(\Delta {l_0} = 6,4\left( {cm} \right);\omega = 10,5\left( {rad/s} \right)\)
-
D.
\(\Delta {l_0} = 6,4\left( {cm} \right);\omega = 13,5\left( {rad/s} \right)\)
Treo một vật có khối lượng m1 vào con lắc lò xo có độ cứng k thì nó dao động với chu kì T1. Nếu treo quả nặng có khối lượng m2 vào lò xo trên thì nó dao động với chu kì T2. Khi treo cả hai vật vào lò xo thì chúng sẽ dao động với chu kì
-
A.
T = T1 + T2
-
B.
\(T = T_1^2 + T_2^2\)
-
C.
\(T = \sqrt {{T_1} + {T_2}} \)
-
D.
\(T = \sqrt {T_1^2 + T_2^2} \)
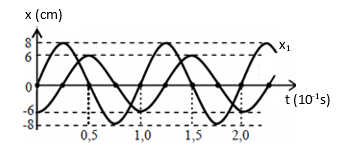
Cho hai dao động điều hoà với li độ x1 và x2 có đồ thị như hình vẽ. Tổng tốc độ của hai dao động ở cùng một thời điểm có giá trị lớn nhất là:
-
A.
140π cm/s
-
B.
200π cm/s
-
C.
280π cm/s
-
D.
20π cm/s.
Một người xách một xô nước đi trên đường, mỗi bước dài 45cm. Chu kì dao động riêng của nước trong xô là 0,3s. Để nước trong xô bị dao động mạnh nhất người đó phải đi với tốc độ
-
A.
3,6m/s.
-
B.
4,2km/s.
-
C.
4,8km/h.
-
D.
5,4km/h.
Một vật dao động điều hòa với chu kỳ T và biên độ là A. Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là?
-
A.
\(\dfrac{T}{2}\)
-
B.
\(\dfrac{T}{4}\)
-
C.
\(\dfrac{T}{6}\)
-
D.
\(\dfrac{T}{8}\)
Dao động điều hoà có vận tốc cực đại là \({v_{max}} = 16\pi cm/s\) và gia tốc cực đại \({a_{max}} = 64{\pi ^2}cm/{s^2}\) thì biên độ của dao động là:
-
A.
$0,25 cm$
-
B.
$2 cm$
-
C.
$4 cm$
-
D.
$16 cm$
Trạng thái của dao động gồm yếu tố nào?
-
A.
Biên độ
-
B.
Li độ \(x\)
-
C.
Chiều chuyển động \(\overrightarrow v \)
-
D.
Cả B và C
Tại một nơi xác định, chu kì dao động điều hòa của con lắc đơn tỉ lệ nghịch với:
-
A.
Căn bậc hai chiều dài con lắc
-
B.
Chiều dài con lắc
-
C.
Căn bậc hai gia tốc trọng trường
-
D.
Gia tốc trọng trường
Chọn phát biểu đúng khi nói về dao động tự do?
-
A.
Tần số của hệ dao động tự do không phụ thuộc vào đặc tính bên trong của hệ
-
B.
Dao động tự do xảy ra dưới tác dụng của ngoại lực kéo về
-
C.
Tần số dao động của hệ dao động tự do phụ thuộc vào đặc tính bên trong của hệ
-
D.
Dao động tự do xảy ra dưới tác dụng của ngoại lực kéo về và tần số của dao động phụ thuộc vào đặc tính bên trong của hệ
Hai dao động vuông pha khi:
-
A.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \)
-
B.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \)
-
C.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \)
-
D.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \alpha \) bất kì
Cho 3 dao động điều hòa cùng phương, cùng tần số \({x_1} = 1,5cos\left( {100\pi t} \right)cm\), \({x_2} = \frac{{\sqrt 3 }}{2}cos\left( {100\pi t + \frac{\pi }{2}} \right)cm\) và \({x_3} = \sqrt 3 cos\left( {100\pi t + \frac{{5\pi }}{6}} \right)cm\). Phương trình dao động tổng hợp của 3 dao động trên là:
-
A.
\(x = \sqrt 3 cos\left( {100\pi t + \frac{\pi }{2}} \right)cm\)
-
B.
\(x = \sqrt 3 cos\left( {200\pi t} \right)cm\)
-
C.
\(x = \sqrt 3 cos\left( {200\pi t + \frac{\pi }{2}} \right)cm\)
-
D.
\(x = \sqrt 3 cos\left( {100\pi t} \right)cm\)
Phát biểu nào sau đây là đúng?
-
A.
Con lắc lò xo dao động điều hòa, cơ năng của con lắc không được bảo toàn
-
B.
Động năng và thế năng của con lắc lò xo dao động điều hòa là không đổi
-
C.
Động năng và thế năng hoặc cùng tăng hoặc cùng giảm
-
D.
Cơ năng của con lắc lò xo dao động điều hòa được bảo toàn, động năng tăng bao nhiêu thì thế năng giảm bấy nhiêu và ngược lại
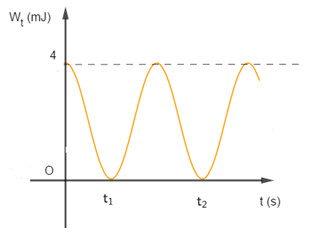
Một con lắc lò xo dao động điều hòa gồm vật nặng có khối lượng \(m = 160g\), đồ thị thế năng theo thời gian của con lắc như hình vẽ. Biết \({t_2} - {t_1} = 0,02s\), lấy \({\pi ^2} = 10\) . Biên độ và chu kì dao động của con lắc là:
-
A.
\(A = 0,8cm,T = 0,04s\)
-
B.
\(A = \sqrt 2 mm,T = 0,04s\)
-
C.
\(A = 0,8cm,T = 0,08s\)
-
D.
\(A = \sqrt 2 mm,T = 0,08s\)
Một con lắc lò xo có độ cứng \(k = 160N/m\), đầu trên cố định còn đầu dưới gắn vật nặng \(m = 1,2kg\). Cho vật \(m\) dao động điều hòa theo phương thẳng đứng thì thấy thời gian lò xo nén trong một chu kì là \(0,14s\). Cho \(g = {\pi ^2} = 10m/{s^2}\). Biên độ dao động của vật là:
-
A.
\(7,5\sqrt 2 cm\)
-
B.
\(7,5 cm\)
-
C.
\(4\sqrt 2 cm\)
-
D.
\(4\sqrt 3 cm\)
Ở một nơi trên Trái Đất, hai con lắc đơn có cùng chiều dài đang dao động điều hòa với cùng biên độ. Gọi \({m_1},{F_1}\) và \({m_2},{F_2}\) lần lượt là khối lượng, độ lớn lực kéo về cực đại của con lắc thứ nhất và con lắc thứ hai. Biết \({m_1} + {m_2} = 1,2\) kg và \(2{F_2} = 3{F_1}\). Giá trị của m1 là
-
A.
720 g.
-
B.
400g
-
C.
480g
-
D.
600g
Cho một vật dao động điều hòa với phương trình \(x = A\cos (\omega t + \varphi )\), giá trị cực tiểu của vận tốc là
-
A.
\(0\)
-
B.
\( - \omega A\)
-
C.
\( - 2\omega A\)
-
D.
\(\omega A\)
Một con lắc lò xo gồm vật nhỏ khối lượng \(m\) và lò xo có độ cứng \(k\) đang dao động điều hòa với biên độ \(A\).Tốc độ cực đại của vật là:
-
A.
\(A.\sqrt {\dfrac{k}{m}} .\)
-
B.
\(\dfrac{{Am}}{k}.\)
-
C.
\(A\sqrt {\dfrac{m}{k}} .\)
-
D.
\(\dfrac{{Ak}}{m}.\)
Lời giải và đáp án
Phát biểu nào sau đây là đúng khi nói về dao động tắt dần?
-
A.
Cơ năng của vật dao động tắt dần giảm dần theo thời gian.
-
B.
Biên độ của vật dao động tắt dần không đổi theo thời gian.
-
C.
Lực cản môi trường tác dụng lên vật luôn sinh công dương.
-
D.
Dao động tắt dần là dao động chỉ chịu tác dụng của nội lực.
Đáp án : A
Ta có: Dao động tắt dần là dao động có biên độ giảm dần theo thời gian
Mặt khác: Cơ năng tỉ lệ thuận với bình phương biên độ:
\({\text{W}} = \frac{1}{2}k{A^2}\)
=> Cơ năng của dao động tắt dần giảm dần theo thời gian
Phát biểu nào sau đây là đúng khi nói về độ lệch pha giữa hai dao động:
-
A.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \): hai dao động ngược pha
-
B.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \): hai dao động cùng pha
-
C.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \) : hai dao động vuông pha
-
D.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \) : Biên độ tổng hợp A = A1+A2
Đáp án : C
Ta có:
+ 2 dao động cùng pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \)
+ 2 dao động ngược pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \)
+ 2 dao động vuông pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \)
Biên độ dao động khi 2 dao động vuông pha:
\({A^2} = A_1^2 + A_2^2\)
Phương trình dao động điều hòa của một chất điểm có dạng \(x = {\rm{ }}Acos\left( a \right)t\) .Độ dài quỹ đạo của dao động là:
-
A.
A
-
B.
2A
-
C.
4A
-
D.
A/2
Đáp án : B
Đồng bộ hóa với phương trình dao động điều hòa và sử dụng công thức xác định quỹ đạo của vật trong dao động điều hòa.
$x = A\cos \left( {\omega t + \varphi } \right)$
Ta có:
+ \(x = Acos\left( a \right)t\)
+ Độ dài quỹ đạo của dao động là: \(L = 2A\)
Khi nói về một vật dao động điều hòa có biên độ $A$ và chu kì $T$, với mốc thời gian $(t = 0)$ là lúc vật ở vị trí biên, phát biểu nào sau đây là sai?
-
A.
Sau thời gian $T/8$, vật đi được quãng đường bằng $0,5A$
-
B.
Sau thời gian $T/2$, vật đi được quãng đường bằng $2A$
-
C.
Sau thời gian $T/4$, vật đi được quãng đường bằng $A$
-
D.
Sau thời gian $T$, vật đi được quãng đường bằng $4A$
Đáp án : A
+ Sử dụng trục thời gian suy ra từ đường tròn
+ Sử phương pháp đại số xác định quãng đường đi được của vật
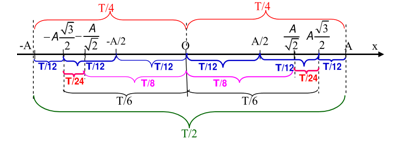
Ta có: t = 0, x0 = A
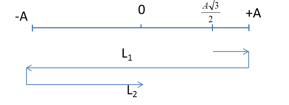
A - sai vì sau T/8 vật ở vị trí có li độ
\(x = \frac{{A\sqrt 2 }}{2} \to S = A - \frac{{A\sqrt 2 }}{2}\)
B, C, D - đúng
Lấy g = π2 = 10 m/s2. Treo con lắc đơn có độ dài ℓ = 100 cm trong thang máy, cho thang máy chuyển động nhanh dần đều đi lên với gia tốc a = 2 m/s2 thì chu kì dao động của con lắc đơn là:
-
A.
Tăng 11,8%.
-
B.
Giảm 16,67%.
-
C.
Giảm 8,7 %.
-
D.
Tăng 25%.
Đáp án : C
+ Áp dụng công thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
+ Áp dụng bài toán con lắc đơn chịu thêm tác dụng của lực quán tính
+ Chu kì dao động của con lắc khi thang máy đứng yên: \(T = 2\pi \sqrt {\frac{l}{g}} \)
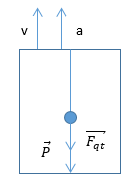
+ Khi thang máy đi lên nhanh dần đều => v,a hướng lên, Fqt hướng xuống
Chu kì dao động của con lắc khi đó:
\(T' = 2\pi \sqrt {\frac{l}{{g'}}} \)
\(\begin{array}{l}g' = g + a = 10 + 2 = 12m/{s^2}\\ \to \frac{{T'}}{T} = \sqrt {\frac{g}{{g'}}} = \sqrt {\frac{{10}}{{12}}} = 0,913 \to T' = 0,913T\end{array}\)
=> Chu kì T’ giảm 1 lượng bằng:
\(\frac{{\Delta T}}{T} = (1 - 0,913) = 0,087 = 8,7\% \)
Cho một chất điểm dao động điều hòa với tần số $1Hz$, thời điểm đầu vật qua vị trí $x = 5cm$ theo chiều dương với tốc độ \(v = 10\pi cm/s\). Viết phương trình dao động.
-
A.
\(x{\text{ }} = {\text{ }}5\sqrt 2 sin(2\pi t{\text{ }} + \frac{\pi }{4}){\text{ }}cm\)
-
B.
\(x = 5\cos (2\pi t - \frac{\pi }{6})cm\)
-
C.
\(x{\text{ }} = {\text{ }}5sin(2\pi t{\text{ }} + \frac{\pi }{4}){\text{ }}cm\)
-
D.
\(x{\text{ }} = {\text{ }}5\sqrt 2 sin(2\pi t{\text{ }} - \frac{\pi }{6}){\text{ }}cm\)
Đáp án : A
- Xác định \(\omega = 2\pi f\)
- Sử dụng hệ thức độc lập xác định biên độ \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)
- Xác định pha ban đầu: Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi \\{\rm{v = - A}}\omega {\rm{sin}}\varphi \end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{{{x_0}}}{A}\\\sin \varphi = - \frac{v}{{A\omega }}\end{array} \right. \to \varphi = ?\)
- Sử dụng công thức lượng giác: \({\rm{cos}}\alpha {\rm{ = sin}}\left( {\alpha + \frac{\pi }{2}} \right)\)
Ta có:
Tốc độ góc: $\omega = 2\pi f = 2\pi .1 = 2\pi (ra{\rm{d}}/s)$
Biên độ dao động:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {5^2} + {\left( {\frac{{10\pi }}{{2\pi }}} \right)^2} \to A = 5\sqrt 2 cm\)
Tại t=0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi = 5\\{\rm{v = - A}}\omega {\rm{sin}}\varphi > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{5}{{5\sqrt 2 }}\\\sin \varphi < 0\end{array} \right. \to \varphi = - \frac{\pi }{4}\)
=> \(x = 5\sqrt 2 {\rm{cos}}\left( {2\pi t - \frac{\pi }{4}} \right)cm = 5\sqrt 2 \sin \left( {2\pi t - \frac{\pi }{4} + \frac{\pi }{2}} \right) = 5\sqrt 2 \sin \left( {2\pi t + \frac{\pi }{4}} \right)cm\)
Một con lắc đơn đang dao động điều hòa với biên độ góc α0 tại nơi có gia tốc trọng trường là g. Biết lực căng dây lớn nhất bằng 1.02 lần lực căng dây nhỏ nhất. Giá trị của α0 là ?
-
A.
3,30
-
B.
6,60
-
C.
5,60
-
D.
9,60
Đáp án : B
+ Áp dụng biểu thức xác định lực căng dây cực đại tại vị trí α = 0:
\({T_{{\rm{max}}}} = mg(3{\rm{ - 2cos}}{\alpha _0})\)
+ Áp dụng biểu thức xác định lực căng dây cực tiểu tại vị trí α = α0:
\({T_{\min }} = mg.c{\rm{os}}{\alpha _0}\)
Ta có:
+ lực căng dây cực đại tại vị trí α = 0:
\({T_{{\rm{max}}}} = mg(3{\rm{ - 2cos}}{\alpha _0})\)
+ lực căng dây cực tiểu tại vị trí α = α0:
\({T_{\min }} = mg.c{\rm{os}}{\alpha _0}\)
\( \to \frac{{{T_{{\rm{max}}}}}}{{{T_{\min }}}} = \frac{{3 - 2c{\rm{os}}{\alpha _0}}}{{{\rm{cos}}{\alpha _0}}} = 1,02 \to c{\rm{os}}{\alpha _0} = 0,993 \to {\alpha _0} = 6,{6^0}\)
Một vật dao động điều hòa với phương trình: \(x = 10c{\rm{os}}\left( {20\pi t - \dfrac{\pi }{6}} \right)cm\). Xác định thời điểm thứ $2016$ vật có gia tốc bằng không?
-
A.
$100,767s$
-
B.
$100,783s$
-
C.
$100,8s$
-
D.
$100,733s$
Đáp án : B
+ Sử dụng công thức xác định chu kỳ $T$: \(T = \dfrac{{2\pi }}{\omega }\)
+ Sử dụng công thức xác định thời điểm vật đi qua li độ x lần thứ $n$ (với $n$ chẵn) : \(t = \dfrac{{n - 2}}{2}T + {t_2}\)
+ Xác định vị trí tại thời điểm $t=0 (x,v)$
Ta có:
Chu kỳ: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{20\pi }} = 0,1s\)
\(\left\{ \begin{gathered}
a = - {\omega ^2}x \hfill \\
a = 0 \hfill \\
\end{gathered} \right. \to x = 0\)
Bài toán đưa về dạng xác định thời điểm vật qua li độ $x=0$ lần thứ $n$ ($n$ chẵn)
=> \({t_{2016}} = \frac{{2016 - 2}}{2}T + {t_2} = 1007T + {t_2}\)
Tại $t=0$: \(\left\{ \begin{array}{l}x = 10c{\rm{os}}\left( {\dfrac{{ - \pi }}{6}} \right) = 5\sqrt 3 cm\\v = - 10.20\pi sin\left( {\dfrac{{ - \pi }}{6}} \right) = 100\pi > 0\end{array} \right.\)
$t_2$ là khoảng thời gian từ lúc bắt đầu đến khi qua $x=0$ lần thứ $2$
=> \({t_2} = \dfrac{T}{{12}} + \dfrac{{3T}}{4} = \dfrac{{5T}}{6}\)
\( \to {t_{2016}} = 1007T + {t_2} = 1007T + \dfrac{{5T}}{6} = \dfrac{{6047T}}{6} = \dfrac{{6047.0,1}}{6} = 100,783{\rm{s}}\)
Một lò xo có độ cứng \(k = 25(N/m)\). Một đầu của lò xo gắn vào điểm O cố định. Treo vào lò xo hai vật có khối lượng \(m = 100g\) và \(∆m = 60g\). Tính độ dãn của lò xo khi vật cân bằng và tần số góc dao động của con lắc.
-
A.
\(\Delta {l_0} = 4,4\left( {cm} \right);\omega = 12,5\left( {rad/s} \right)\)
-
B.
\(\Delta {l_0} = 6,4\left( {cm} \right);\omega = 12,5\left( {rad/s} \right)\)
-
C.
\(\Delta {l_0} = 6,4\left( {cm} \right);\omega = 10,5\left( {rad/s} \right)\)
-
D.
\(\Delta {l_0} = 6,4\left( {cm} \right);\omega = 13,5\left( {rad/s} \right)\)
Đáp án : B
+ Áp dụng biểu thức xác định độ dãn của lò xo treo thẳng đứng tại vị trí cân bằng: \(\Delta l = \dfrac{{mg}}{k}\)
+ Áp dụng biểu thức xác định tần số góc dao động của con lắc lò xo: \(\omega = \sqrt {\dfrac{k}{m}} \)
Ta có, độ dãn của lò xo tại vị trí cân bằng:
\(\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,16.10}}{{25}} = 0,064m = 6,4cm\)
Tần số góc dao động của con lắc:
\(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{25}}{{0,16}}} = 12,5(ra{\rm{d}}/s)\)
Treo một vật có khối lượng m1 vào con lắc lò xo có độ cứng k thì nó dao động với chu kì T1. Nếu treo quả nặng có khối lượng m2 vào lò xo trên thì nó dao động với chu kì T2. Khi treo cả hai vật vào lò xo thì chúng sẽ dao động với chu kì
-
A.
T = T1 + T2
-
B.
\(T = T_1^2 + T_2^2\)
-
C.
\(T = \sqrt {{T_1} + {T_2}} \)
-
D.
\(T = \sqrt {T_1^2 + T_2^2} \)
Đáp án : D
Xem nội dung mục 3 - phần II : Sự thay đổi chu kì - tần số - tần số góc theo khối lượng vật nặng
Ta có: \(T = 2\pi \sqrt {\frac{m}{k}} \to {T^2} \sim m\)
=> Khi treo cả hai vật vào lò xo thì chu kì dao động là: \(T = \sqrt {T_1^2 + T_2^2} \)
Cho hai dao động điều hoà với li độ x1 và x2 có đồ thị như hình vẽ. Tổng tốc độ của hai dao động ở cùng một thời điểm có giá trị lớn nhất là:

-
A.
140π cm/s
-
B.
200π cm/s
-
C.
280π cm/s
-
D.
20π cm/s.
Đáp án : B
+ Sử dụng lí thuyết về hai dao động điều hoà cùng tần số
+ Áp dụng biểu thức tính vận tốc cực đại: \({v_{m{\rm{ax}}}} = \omega .A\)
Phương trình chất điểm 1 : là \({x_1} = 8\cos \left( {20\pi t - \frac{\pi }{2}} \right)cm\)
Phương trình chất điểm 2 là :
\({x_2} = 6\cos \left( {20\pi t + \pi } \right)cm\)
Hai chất điểm vuông pha :
\( \Rightarrow A = \sqrt {A_1^2 + A_2^2} = 10\)
Vận tốc lớn nhất :
\({v_{m{\rm{ax}}}} = \omega .A = 20\pi .10 = 200\pi cm/s\)
Một người xách một xô nước đi trên đường, mỗi bước dài 45cm. Chu kì dao động riêng của nước trong xô là 0,3s. Để nước trong xô bị dao động mạnh nhất người đó phải đi với tốc độ
-
A.
3,6m/s.
-
B.
4,2km/s.
-
C.
4,8km/h.
-
D.
5,4km/h.
Đáp án : D
+ Vận dụng lí thuyết cộng hưởng
+ Áp dụng công thức \(v = \frac{S}{t}\)
Để nước trong xô bị dao động mạnh nhất thì phải xảy ra cộng hưởng cơ
=> T = T0 = 0,3s
Tốc độ khi đó:
\(v = \frac{S}{t} = \frac{{0,45}}{{0,3}} = 1,5m/s = 5,4km/h\)
Một vật dao động điều hòa với chu kỳ T và biên độ là A. Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là?
-
A.
\(\dfrac{T}{2}\)
-
B.
\(\dfrac{T}{4}\)
-
C.
\(\dfrac{T}{6}\)
-
D.
\(\dfrac{T}{8}\)
Đáp án : B
+ Áp dụng biểu thức xác định cơ năng:
\({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\)
+ Sử dụng trục thời gian suy ra từ vòng tròn
Ta có:
\({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x = \pm \dfrac{A}{{\sqrt 2 }}\)
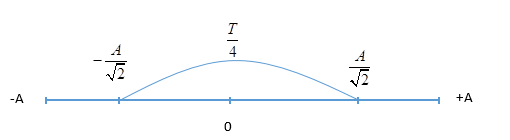
Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\dfrac{T}{4}\)
Dao động điều hoà có vận tốc cực đại là \({v_{max}} = 16\pi cm/s\) và gia tốc cực đại \({a_{max}} = 64{\pi ^2}cm/{s^2}\) thì biên độ của dao động là:
-
A.
$0,25 cm$
-
B.
$2 cm$
-
C.
$4 cm$
-
D.
$16 cm$
Đáp án : C
Sử dụng công thức xác định gia tốc cực đại và vận tốc cực đại trong dao động điều hòa:
\({v_{max}} = A\omega ,{\rm{ }}{a_{max}} = {\omega ^2}A\)
Ta có: $\left\{ \begin{gathered}{v_{{\text{max}}}} = \omega A \hfill \\{a_{{\text{max}}}} = {\omega ^2}A \hfill \\\end{gathered} \right. \to \dfrac{{{v^2}_{{\text{max}}}}}{{{a_{{\text{max}}}}}} = \dfrac{{{{(\omega A)}^2}}}{{{\omega ^2}A}} = A = \dfrac{{{{\left( {16\pi } \right)}^2}}}{{64\pi^2 }} = 4cm$
Trạng thái của dao động gồm yếu tố nào?
-
A.
Biên độ
-
B.
Li độ \(x\)
-
C.
Chiều chuyển động \(\overrightarrow v \)
-
D.
Cả B và C
Đáp án : D
Pha của dao động \(\left( {\omega t + \varphi } \right)\)cho biết trạng thái dao động (gồm li độ \(x\) và chiều chuyển động \(\overrightarrow v \) )
Tại một nơi xác định, chu kì dao động điều hòa của con lắc đơn tỉ lệ nghịch với:
-
A.
Căn bậc hai chiều dài con lắc
-
B.
Chiều dài con lắc
-
C.
Căn bậc hai gia tốc trọng trường
-
D.
Gia tốc trọng trường
Đáp án : C
Vận dụng biểu thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
Ta có chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
=> Chu kì dao động của con lăc đơn tỉ lệ thuận với căn bậc 2 chiều dài con lắc và tỉ lệ nghịch với căn bậc hai gia tốc trọng trường
Chọn phát biểu đúng khi nói về dao động tự do?
-
A.
Tần số của hệ dao động tự do không phụ thuộc vào đặc tính bên trong của hệ
-
B.
Dao động tự do xảy ra dưới tác dụng của ngoại lực kéo về
-
C.
Tần số dao động của hệ dao động tự do phụ thuộc vào đặc tính bên trong của hệ
-
D.
Dao động tự do xảy ra dưới tác dụng của ngoại lực kéo về và tần số của dao động phụ thuộc vào đặc tính bên trong của hệ
Đáp án : C
Ta có: Dao động tự do là hệ dao động xảy ra dưới tác dụng của nội lực kéo về và tần số dao động của hệ chỉ phụ thuộc vào đặc tính bên trong của hệ.
=> Các phương án
+ A, B, D – sai
+ C - đúng
Hai dao động vuông pha khi:
-
A.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \)
-
B.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \)
-
C.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \)
-
D.
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \alpha \) bất kì
Đáp án : C
Hai dao động vuông pha khi: \(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \)
Cho 3 dao động điều hòa cùng phương, cùng tần số \({x_1} = 1,5cos\left( {100\pi t} \right)cm\), \({x_2} = \frac{{\sqrt 3 }}{2}cos\left( {100\pi t + \frac{\pi }{2}} \right)cm\) và \({x_3} = \sqrt 3 cos\left( {100\pi t + \frac{{5\pi }}{6}} \right)cm\). Phương trình dao động tổng hợp của 3 dao động trên là:
-
A.
\(x = \sqrt 3 cos\left( {100\pi t + \frac{\pi }{2}} \right)cm\)
-
B.
\(x = \sqrt 3 cos\left( {200\pi t} \right)cm\)
-
C.
\(x = \sqrt 3 cos\left( {200\pi t + \frac{\pi }{2}} \right)cm\)
-
D.
\(x = \sqrt 3 cos\left( {100\pi t} \right)cm\)
Đáp án : A
+ Sử dụng lí thuyết về tổng hợp hai dao động điều cùng phương, cùng tần số
+ Tổng hợp từng 2 dao động một: \(x{\rm{ }} = {\rm{ }}{x_1} + {\rm{ }}{x_2} + {\rm{ }}{x_3} = {\rm{ }}{x_{12}} + {\rm{ }}{x_3}\)
Phương trình dao động tổng hợp của 3 dao động trên: \(x{\rm{ }} = {\rm{ }}{x_1} + {\rm{ }}{x_2} + {\rm{ }}{x_3} = {\rm{ }}{x_{12}} + {\rm{ }}{x_3}\)
Phương trình dao động tổng hợp của 1 và 2 có dạng: \({x_{12}} = {A_{12}}\cos (100\pi t + {\varphi _{12}})\) trong đó:
\({A_{12}} = \sqrt {A_1^2 + A_2^2} = \sqrt 3 (cm)\)(vì hai dao động vuông pha)
\(\tan {\varphi _{12}} = \frac{{{A_2}}}{{{A_1}}} = \frac{{\sqrt 3 }}{3} = > {\varphi _{12}} = \frac{\pi }{6}(rad)\)
Vậy \({x_{12}} = \sqrt 3 \cos (100\pi t + \frac{\pi }{6})cm\)
- Dao động tổng hợp của ba dao động có phương trình \(x = {x_{12}} + {x_3} = A\cos (100\pi t + \varphi )\) trong đó:
\(A = \sqrt {A_{12}^2 + A_3^2 + 2{A_{12}}{A_3}\cos ({\varphi _3} - {\varphi _{12}})} = \sqrt {3 + 3 + 2\sqrt 3 \sqrt 3 \cos (\frac{{5\pi }}{6} - \frac{\pi }{6})} = \sqrt 3 (cm)\)
\(\tan \varphi = \frac{{{A_{12}}\sin {\varphi _{12}} + {A_2}\sin {\varphi _3}}}{{{A_{12}}\cos {\varphi _{12}} + {A_2}\cos {\varphi _3}}}\)(không xác định)
\( \to \varphi = \frac{\pi }{2}\left( {rad} \right)\)
Vậy phương trình dao động tổng hợp là: \(x = \sqrt 3 \cos (100\pi t + \frac{\pi }{2})cm\)
Phát biểu nào sau đây là đúng?
-
A.
Con lắc lò xo dao động điều hòa, cơ năng của con lắc không được bảo toàn
-
B.
Động năng và thế năng của con lắc lò xo dao động điều hòa là không đổi
-
C.
Động năng và thế năng hoặc cùng tăng hoặc cùng giảm
-
D.
Cơ năng của con lắc lò xo dao động điều hòa được bảo toàn, động năng tăng bao nhiêu thì thế năng giảm bấy nhiêu và ngược lại
Đáp án : D
Sử dụng lí thuyết và biểu thức tính cơ năng
A – sai vì: Cơ năng của con lắc lò xo dao động điều hòa được bảo toàn
B – sai vì: Động năng và thế năng của con lắc lò xo luôn thay đổi
C – sai vì: Trong dao động điều hòa của con lắc lò xo, động năng tăng bao nhiêu thì thế năng giảm bấy nhiêu.
D - đúng
Một con lắc lò xo dao động điều hòa gồm vật nặng có khối lượng \(m = 160g\), đồ thị thế năng theo thời gian của con lắc như hình vẽ. Biết \({t_2} - {t_1} = 0,02s\), lấy \({\pi ^2} = 10\) . Biên độ và chu kì dao động của con lắc là:

-
A.
\(A = 0,8cm,T = 0,04s\)
-
B.
\(A = \sqrt 2 mm,T = 0,04s\)
-
C.
\(A = 0,8cm,T = 0,08s\)
-
D.
\(A = \sqrt 2 mm,T = 0,08s\)
Đáp án : B
+ Đọc đồ thị \({W_t} - {\rm{ }}t\)
+ Thế năng dao động tuần hoàn với chu kì: \(T' = \dfrac{T}{2}\)
+ Áp dụng biểu thức tính thế năng cực đại: \({{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2}\)
Gọi \(T'\): chu kì tuần hoàn của thế năng
\(T\): chu kì dao động của vật
Ta có: \(T' = \dfrac{T}{2}\)
Từ đồ thị Wt - t, ta có:
\(\begin{array}{l}{t_2} - {t_1} = {\rm{ }}0,02s = T' = \dfrac{T}{2} \to T = 0,04s\\ \to \omega = \dfrac{{2\pi }}{T} = 50\pi \left( {rad/s} \right)\end{array}\)
\(\begin{array}{l}{{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2} = {4.10^{ - 3}}\\ \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{t_{{\rm{max}}}}}}}}{{m{\omega ^2}}}} = \sqrt {\dfrac{{{{2.4.10}^{ - 3}}}}{{0,16{{(50\pi )}^2}}}} = \sqrt 2 {.10^{ - 3}}m = \sqrt 2 mm\end{array}\)
Một con lắc lò xo có độ cứng \(k = 160N/m\), đầu trên cố định còn đầu dưới gắn vật nặng \(m = 1,2kg\). Cho vật \(m\) dao động điều hòa theo phương thẳng đứng thì thấy thời gian lò xo nén trong một chu kì là \(0,14s\). Cho \(g = {\pi ^2} = 10m/{s^2}\). Biên độ dao động của vật là:
-
A.
\(7,5\sqrt 2 cm\)
-
B.
\(7,5 cm\)
-
C.
\(4\sqrt 2 cm\)
-
D.
\(4\sqrt 3 cm\)
Đáp án : A
+ Sử dụng công thức tính độ dãn của lò xo ở VTCB: \(\Delta l = \dfrac{{mg}}{k}\)
+ Sử dụng công thức tính chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{m}{k}} \)
+ Vận dụng tỉ số thời gian nén trên chu kì => tỉ lệ => Biên độ
Ta có:
+ Độ dãn của lò xo ở VTCB: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{{1,2.10}}{{160}} = 0,075m = 7,5cm\)
Chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{m}{k}} = 2\pi \sqrt {\dfrac{{1,2}}{{160}}} \approx 0,55{\rm{s}}\)
\(\dfrac{{{t_n}}}{T} = \dfrac{{0,14}}{{0,55}} \approx 0,25 \to {t_n} = 0,25T = \dfrac{T}{4}\)
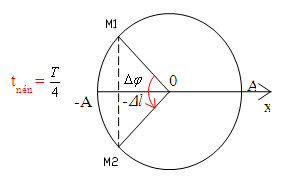
Ta có: \(\Delta \varphi = \omega \Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{4} = \dfrac{\pi }{2}\)
\(\begin{array}{l} \to \Delta l = Acos\dfrac{{\Delta \varphi }}{2} = Acos\dfrac{\pi }{4} = \dfrac{A}{{\sqrt 2 }}\\ \to A = \sqrt 2 \Delta l = 7,5\sqrt 2 cm\end{array}\)
Ở một nơi trên Trái Đất, hai con lắc đơn có cùng chiều dài đang dao động điều hòa với cùng biên độ. Gọi \({m_1},{F_1}\) và \({m_2},{F_2}\) lần lượt là khối lượng, độ lớn lực kéo về cực đại của con lắc thứ nhất và con lắc thứ hai. Biết \({m_1} + {m_2} = 1,2\) kg và \(2{F_2} = 3{F_1}\). Giá trị của m1 là
-
A.
720 g.
-
B.
400g
-
C.
480g
-
D.
600g
Đáp án : C
Áp dụng công thức của lực kéo về:
\(\begin{array}{l}{F_{kv}} = - mg\sin \alpha \approx - mg\alpha = - mg\dfrac{s}{\ell } = - m{\omega ^2}s\\ \Rightarrow {F_{kv\max }} = m{\omega ^2}s_o\end{array}\)
Ta có, lực kéo về cực đại: \({F_{kv\max }} = m{\omega ^2}s_o\)
\(\begin{array}{l}\left\{ \begin{array}{l}{F_{1\max }} = {m_1}{\omega ^2}s_0\\{F_{2\max }} = {m_2}{\omega ^2}s_0\end{array} \right.\\ \Rightarrow \dfrac{{{F_{1\max }}}}{{{F_{2\max }}}} = \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{{m_1}}}{{1,2 - {m_1}}} = \dfrac{2}{3}\\ \Rightarrow {m_1} = 0,48kg = 480g\end{array}\)
Cho một vật dao động điều hòa với phương trình \(x = A\cos (\omega t + \varphi )\), giá trị cực tiểu của vận tốc là
-
A.
\(0\)
-
B.
\( - \omega A\)
-
C.
\( - 2\omega A\)
-
D.
\(\omega A\)
Đáp án : B
Giá trị cực tiểu của vận tốc là: \( - \omega A\)
Giá trị cực tiểu của vận tốc là: \( - \omega A\)
Một con lắc lò xo gồm vật nhỏ khối lượng \(m\) và lò xo có độ cứng \(k\) đang dao động điều hòa với biên độ \(A\).Tốc độ cực đại của vật là:
-
A.
\(A.\sqrt {\dfrac{k}{m}} .\)
-
B.
\(\dfrac{{Am}}{k}.\)
-
C.
\(A\sqrt {\dfrac{m}{k}} .\)
-
D.
\(\dfrac{{Ak}}{m}.\)
Đáp án : A
Sử dụng biểu thức tính tốc độ cực đại: \(v = \omega A\)
Tốc độ góc của con lắc: \(\omega = \sqrt {\dfrac{k}{m}} \)
Tốc độ cực đại của vật là \({v_{{\rm{max}}}} = \omega A = A.\sqrt {\dfrac{k}{m}} \)
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận