Đề kiểm tra 1 tiết chương 3: Dòng điện xoay chiều - Đề số 01
Đề bài
Mạch điện nối tiếp gồm R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C thay đổi. Điện áp hai đầu ổn định là U, tần số f. Khi UC cực đại, dung kháng ZC có giá trị là:
-
A.
\({Z_C} = \dfrac{{\sqrt {{R^2} + Z_L^2} }}{{{Z_L}}}\)
-
B.
\({Z_C} = R + {Z_L}\)
-
C.
\({Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}\)
-
D.
\({Z_C} = \dfrac{{{R^2} + Z_L^2}}{R}\)
Nguyên tắc hoạt động của máy phát điện xoay chiều một pha dựa vào
-
A.
Hiện tượng cảm ứng điện từ
-
B.
Hiện tượng cộng hưởng
-
C.
Hiện tượng tự cảm
-
D.
Hiện tượng giao thoa.
Trong mạch R, L, C nối tiếp với điện áp hai đầu đoạn mạch là u và cường độ dòng điện qua mạch là i. Chọn phát biểu đúng:
-
A.
Nếu ZL > ZC thì u sớm pha hơn i là \(\frac{\pi }{2}\)
-
B.
Nếu ZL < ZC thì i chậm pha hơn u \(\frac{\pi }{2}\)
-
C.
Nếu R = 0 thì u cùng pha với i.
-
D.
Nếu ZL = ZC thì u cùng pha với i.
Phát biểu nào sau đây sai về máy biến áp:
-
A.
Là dụng cụ dùng để thay đổi điện áp của dòng điện xoay chiều.
-
B.
Cấu tạo gồm hai cuộn dây đồng quấn trên lõi thép.
-
C.
Cường độ dòng điện qua mỗi dây tỉ lệ thuận với số vòng dây.
-
D.
Nguyên tắc hoạt động dựa vào hiện tượng cảm ứng điện từ.
Một khung dây dẫn có diện tích $S = 50 cm^2$ gồm $150$ vòng dây quay đều với vận tốc n vòng/phút trong một từ trường đều \(\vec B\) vuông góc trục quay \(\Delta \) và có độ lớn $B = 0,02 T$. Từ thông cực đại gửi qua khung là:
-
A.
$0,015 Wb$
-
B.
$0,15 Wb$
-
C.
$1,5 Wb$
-
D.
$15 Wb$
Một mạch điện xoay chiều RLC nối tiếp. Điện áp ở hai đầu đoạn mạch \(u = {U_0}\cos \omega t\), cho biết \(LC{\omega ^2} = 1\). Nếu ta tăng tần số góc \(\omega \) của u thì
-
A.
Công suất tiêu thụ của mạch điện tăng
-
B.
Cường độ hiệu dụng qua mạch giảm
-
C.
Tổng trở của đoạn mạch giảm
-
D.
Hệ số công suất của mạch tăng.
Mạch điện xoay chiều nối tiếp AB theo đúng thứ tự gồm cuộn cảm thuần L, điện trở thuần R và tụ điện C. Cho biết điện áp hiệu dụng \({U_{RL}} = {U_{RC}}\sqrt 3 \) và R2 = L/C. Tính hệ số công suất của đoạn mạch AB.
-
A.
\(\dfrac{{\sqrt 2 }}{7}\)
-
B.
\(\dfrac{{\sqrt 3 }}{5}\)
-
C.
\(\sqrt {\dfrac{3}{7}} \)
-
D.
\(\dfrac{{\sqrt 2 }}{5}\)
Cho đoạn mạch RLC mắc nối tiếp , cuộn dây cảm thuần, điện trở R thay đổi được. Đặt hai đầu đoạn mạch một điện áp xoay chiều có điện áp hiệu dụng là 200V. Khi R = R1 và R = R2 thì mạch có cùng công suất. Biết \({R_1} + {\rm{ }}{R_2} = {\rm{ }}100\Omega .\) Khi R = R1 công suất của mạch là:
-
A.
400 W
-
B.
220 W
-
C.
440W
-
D.
880 W
Một chiếc đèn neon đặt dưới một điện áp xoay chiều $119V-50Hz$. Nó chỉ sáng lên khi điện áp tức thời giữa hai đầu bóng đèn có trị tuyệt đối lớn hơn $84V$. Thời gian bóng đèn sáng trong một chu kì là bao nhiêu?
-
A.
\(\Delta t = 0,0100s\)
-
B.
\(\Delta t = 0,0133s\)
-
C.
\(\Delta t = 0,0200s\)
-
D.
\(\Delta t = 0,0233s\)
Người ta cần truyền một công suất điện một pha 100kW dưới một hiệu điện thế hiệu dụng 5kV đi xa. Mạch điện có hệ số công suất \(cos\varphi = {\rm{ }}0,8\Omega \) . Muốn cho tỷ lệ năng lượng mất trên đường dây không quá 10% thì điện trở của đường dây phải có giá trị trong khoảng nào?
-
A.
10Ω≤ R ≤12Ω
-
B.
R ≤ 14 Ω
-
C.
R ≤16 Ω
-
D.
16Ω ≤ R ≤ 18 Ω
Cho một đoạn mạch điện xoay chiều chỉ có cuộn cảm thuần. Tại thời điểm t1 điện áp và dòng điện qua cuộn cảm có giá trị lần lượt là 25 V; 0,3 A. Tại thời điểm t2 điện áp và dòng điện qua cuộn cảm có giá trị lần lượt là 15 V; 0,5 A. Cảm kháng của mạch có giá trị là:
-
A.
30 Ω.
-
B.
50 Ω.
-
C.
40 Ω.
-
D.
100 Ω.
Xét một mạch điện gồm một động cơ điện ghép nối tiếp với một tụ điện. Đặt vào hai đầu mạch một điện áp xoay chiều có giá trị hiệu dụng U= 100V thì mạch có hệ số công suất là 0,9. Lúc này động cơ hoạt động bình thường với hiệu suất 80% và hệ số công suất 0,75. Biết điện trở trong của động cơ là 10Ω. Điện áp hiệu dụng hai đầu động cơ và cường độ dòng điện hiệu dụng qua động cơ lần lượt:
-
A.
120V,6A
-
B.
125V,6A
-
C.
120V,1,8A
-
D.
125V, 1,8A
Cho đoạn mạch AB gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp; trong đó R và C không đổi, còn L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = U\sqrt 2 {\rm{cos(}}\omega {\rm{t + }}{\varphi _u})\) (với \(U,\omega \) không đổi). Điều chỉnh L tới giá trị L1 thì hiệu điện thế hiệu dụng hai đầu cuộn cảm đạt giá trị cực đại và bằng ULmax. Gọi UCmax là giá trị hiệu điện thế hiệu dụng cực đại ở hai đầu tụ điện. Cho biết \({U_{L\max }} = \sqrt 5 {U_{Rm{\rm{ax}}}}\) . Hệ thức nào sau đây là đúng?
-
A.
\(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{2}{{\sqrt 5 }}\)
-
B.
\(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{{\sqrt 5 }}{2}\)
-
C.
\(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{1}{{\sqrt 5 }}\)
-
D.
\(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{1}{{2\sqrt 5 }}\)
Một mạch điện xoay chiều có u là điện áp tức thời ở hai đầu đoạn mạch và i là cường độ tức thời qua mạch. Chọn phát biểu sai.
-
A.
u và i luôn biến thiên cùng tần số
-
B.
Mạch chỉ có điện trở u và i vuông pha
-
C.
Mạch chỉ có cuộn cảm thuần u sớm pha hơn i một góc \(\frac{\pi }{2}\)
-
D.
Mạch chỉ có tụ điện u trễ pha hơn i một góc \(\frac{\pi }{2}\)
Khái niệm cường độ dòng điện hiệu dụng được xây dựng dựa trên tác dụng nào của dòng điện?
-
A.
Tác dụng hóa học của dòng điện.
-
B.
Tác dụng nhiệt của dòng điện.
-
C.
Tác dụng từ của dòng điện.
-
D.
Tác dụng phát quang của dòng điện.
Trường hợp nào sau đây có thể dùng dòng điện xoay chiều để sử dụng?
-
A.
Mạ điện
-
B.
Đúc điện
-
C.
Đèn điện dây tóc
-
D.
Điều chế kim loại bằng điện phân
Đoạn mạch RLC nối tiếp \(R = 40\Omega \); \(L = \dfrac{{0,4}}{\pi }(H)\)và \(C = \dfrac{{{{10}^{ - 3}}}}{\pi }(F)\). Cho tần số dòng điện là \(50{\rm{ }}Hz\) và điện áp hiệu dụng ở hai đầu R là \(40{\rm{ }}V\). Điện áp ở hai đầu đoạn mạch là:
-
A.
100 V
-
B.
150 V
-
C.
200 V
-
D.
50 V
Biết cường độ dòng điện qua đoạn mạch chỉ có điện trở có biểu thức \(i = {I_0}cos\left( {\omega t} \right)A\). Biểu thức điện áp đặt vào hai đầu đoạn mạch là:
-
A.
\(u = {I_0}Rcos\left( {\omega t + \dfrac{\pi }{2}} \right)V\)
-
B.
\(u = \dfrac{{{I_0}}}{R}cos\left( {\omega t} \right)V\)
-
C.
\(u = \dfrac{{{I_0}}}{R}cos\left( {\omega t + \dfrac{\pi }{2}} \right)V\)
-
D.
\(u = {I_0}Rcos\left( {\omega t} \right)V\)
Đồ thị cường độ dòng điện như hình vẽ
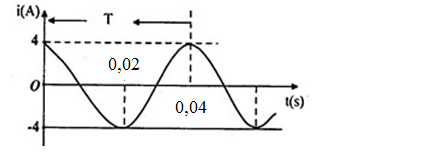
Cường độ dòng điện tức thời có biểu thức
-
A.
\(i = 4c{\rm{os}}\left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
-
B.
\(i = 4c{\rm{os}}\left( {50\pi t} \right)A\)
-
C.
\(i = 4c{\rm{os}}\left( {100\pi t} \right)A\)
-
D.
\(i = 4c{\rm{os}}\left( {50\pi t + \dfrac{\pi }{2}} \right)A\)
Cuộn dây có điện trở thuần \(R = 50\Omega \) và độ tự cảm L mắc vào điện áp xoay chiều \(U = 110{\rm{ }}V\) có tần số \(f = 60Hz\). Cho biết công suất của mạch điện là \(100W\). Giá trị của L là:
-
A.
\(0,637H\)
-
B.
\(0,318H\)
-
C.
\(0,5H\)
-
D.
\(0,158H\)
Mạch điện nối tiếp gồm điện trở \(R\), cuộn dây thuần cảm có độ tự cảm \(L\) và tụ điện có điện dung \(C\) thay đổi được . Điện áp hai đầu là \(U\) ổn định, tần số \(f\). Thay đổi \(C\) để \({U_{Cmax}}\). Chọn hệ thức sai?
-
A.
\(U_{Cm{\rm{ax}}}^2 = {U^2} + U_R^2 + U_L^2\)
-
B.
\(U_{Cm{\rm{ax}}}^2 = {U^2} + U_{RL}^2\)
-
C.
\({U_{{C_{max}}}}.{U_R} = U.{U_{RL}}\)
-
D.
\(\dfrac{1}{{U_{{C_{max}}}^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\)
Trên đoạn mạch xoay chiều không phân nhánh có 4 điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có cuộn cảm thuần, giữa hai điểm M và N chỉ có điện trở thuần, giữa hai điểm N và B chỉ có tụ điện. Điện áp hiệu dụng giữa hai điểm A và N là \(400{\rm{ }}V\) và điện áp hiệu dụng giữa hai điểm M và B là \(300{\rm{ }}V\). Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau \({90^0}\). Biết cường độ dòng điện hiệu dụng trong mạch có giá trị \(3\sqrt 2 A\). Giá trị của điện trở R là:
-
A.
\(80\Omega \)
-
B.
\(25\sqrt 2 \Omega \)
-
C.
\(30\sqrt 2 \Omega \)
-
D.
\(40\sqrt 2 \Omega \)
Một đoạn mạch điện gồm một cuộn dây thuần cảm có độ tự cảm \(L = 1/π (H)\) và điện trở thuần \(R = 100 Ω\). Đặt vào hai đầu mạch một điện áp xoay chiều \(u = 200cos(100πt + π/4) V\) thì biểu thức nào sau đây là của điện áp hai đầu cuộn cảm thuần ?
-
A.
\({u_L} = 100\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{4}} \right)V\)
-
B.
\({u_L} = 100cos\left( {100\pi t + \dfrac{\pi }{2}} \right)V\)
-
C.
\({u_L} = 100\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{2}} \right)V\)
-
D.
\({u_L} = 100\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{2}} \right)V\)
Cuộn sơ cấp và cuộn thứ cấp của một máy biến áp lí tưởng có số vòng dây lần lượt là N1 và N2. Đặt điện áp xoay chiều có giá trị hiệu dụng U1 vào hai đầu cuộn sơ cấp thì điện áp hiệu dụng giữa hai đầu cuộn thứ cấp để hở là U2. Hệ thức đúng là:
-
A.
\(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_2}}}{{{N_1}}}\)
-
B.
\(\dfrac{{{U_1}}}{{{N_1}}} = {U_2}{N_2}\)
-
C.
\({U_1}{U_2} = {N_1}{N_2}\).
-
D.
\(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}}\)
Đặt điện áp xoay chiều \(u = {U_0}\cos \omega t\) vào hai đầu đoạn mạch chỉ có điện trở thuần. Gọi U là điện áp hiệu dụng giữa hai đầu đoạn mạch; i, I0 và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường độ dòng điện trong đoạn mạch. Hệ thức nào sau đây sai?
-
A.
\(\dfrac{U}{{{U_0}}} - \dfrac{I}{{{I_0}}} = 0\)
-
B.
\(\dfrac{U}{{{U_0}}} + \dfrac{I}{{{I_0}}} = \sqrt 2 \)
-
C.
\(\dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1\)
-
D.
\(\dfrac{u}{U} - \dfrac{i}{I} = 0\)
Lời giải và đáp án
Mạch điện nối tiếp gồm R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C thay đổi. Điện áp hai đầu ổn định là U, tần số f. Khi UC cực đại, dung kháng ZC có giá trị là:
-
A.
\({Z_C} = \dfrac{{\sqrt {{R^2} + Z_L^2} }}{{{Z_L}}}\)
-
B.
\({Z_C} = R + {Z_L}\)
-
C.
\({Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}\)
-
D.
\({Z_C} = \dfrac{{{R^2} + Z_L^2}}{R}\)
Đáp án : C
C thay đổi để UC max, khi đó: \({Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}\)
Nguyên tắc hoạt động của máy phát điện xoay chiều một pha dựa vào
-
A.
Hiện tượng cảm ứng điện từ
-
B.
Hiện tượng cộng hưởng
-
C.
Hiện tượng tự cảm
-
D.
Hiện tượng giao thoa.
Đáp án : A
Xem lí thuyết phần 1
Nguyên tắc hoạt động máy phát điện xoay chiều dựa trên hiện tượng cảm ứng điện từ
Trong mạch R, L, C nối tiếp với điện áp hai đầu đoạn mạch là u và cường độ dòng điện qua mạch là i. Chọn phát biểu đúng:
-
A.
Nếu ZL > ZC thì u sớm pha hơn i là \(\frac{\pi }{2}\)
-
B.
Nếu ZL < ZC thì i chậm pha hơn u \(\frac{\pi }{2}\)
-
C.
Nếu R = 0 thì u cùng pha với i.
-
D.
Nếu ZL = ZC thì u cùng pha với i.
Đáp án : D
A - sai vì ZL > ZC ta chỉ có thể kểt luận là u sớm pha hơn i
B- sai vì ZL < ZC ta chỉ có thể kết luận là u chậm pha hơn i
C - sai vì R = 0 thì u và i không thể cùng pha
D- đúng
Phát biểu nào sau đây sai về máy biến áp:
-
A.
Là dụng cụ dùng để thay đổi điện áp của dòng điện xoay chiều.
-
B.
Cấu tạo gồm hai cuộn dây đồng quấn trên lõi thép.
-
C.
Cường độ dòng điện qua mỗi dây tỉ lệ thuận với số vòng dây.
-
D.
Nguyên tắc hoạt động dựa vào hiện tượng cảm ứng điện từ.
Đáp án : C
A, B, D - đúng
C - sai vì cường độ dòng điện qua mỗi dây tỉ lệ nghịch với số vòng dây
Một khung dây dẫn có diện tích $S = 50 cm^2$ gồm $150$ vòng dây quay đều với vận tốc n vòng/phút trong một từ trường đều \(\vec B\) vuông góc trục quay \(\Delta \) và có độ lớn $B = 0,02 T$. Từ thông cực đại gửi qua khung là:
-
A.
$0,015 Wb$
-
B.
$0,15 Wb$
-
C.
$1,5 Wb$
-
D.
$15 Wb$
Đáp án : A
Áp dụng dụng biểu thức xác định từ thông cực đại qua khung: $Φo = NBS$
Ta có từ thông cực đại qua khung:
\(\Phi o = NBS = 150.0,02.({50.10^{ - 4}}) = 0,015{\rm{W}}b\)
Đổi đơn vị của diện tích: cm2 sang m2
Một mạch điện xoay chiều RLC nối tiếp. Điện áp ở hai đầu đoạn mạch \(u = {U_0}\cos \omega t\), cho biết \(LC{\omega ^2} = 1\). Nếu ta tăng tần số góc \(\omega \) của u thì
-
A.
Công suất tiêu thụ của mạch điện tăng
-
B.
Cường độ hiệu dụng qua mạch giảm
-
C.
Tổng trở của đoạn mạch giảm
-
D.
Hệ số công suất của mạch tăng.
Đáp án : B
Theo đầu bài, ta có:
\(LC{\omega ^2} = 1 \to {Z_L} = {Z_C}\)
=> Công suất của mạch cực đại
Nếu ta tăng tần số góc \(\omega \)thì:
+ Công suất tiêu thụ của mạch giảm
+ Cường độ hiệu dụng qua mạch giảm:
\(I = \frac{U}{Z}\)
+ Tổng trở của đoạn mạch tăng
+ Hệ số công suất của mạch giảm
Ta suy ra:
A, C, D - sai
B- đúng
Mạch điện xoay chiều nối tiếp AB theo đúng thứ tự gồm cuộn cảm thuần L, điện trở thuần R và tụ điện C. Cho biết điện áp hiệu dụng \({U_{RL}} = {U_{RC}}\sqrt 3 \) và R2 = L/C. Tính hệ số công suất của đoạn mạch AB.
-
A.
\(\dfrac{{\sqrt 2 }}{7}\)
-
B.
\(\dfrac{{\sqrt 3 }}{5}\)
-
C.
\(\sqrt {\dfrac{3}{7}} \)
-
D.
\(\dfrac{{\sqrt 2 }}{5}\)
Đáp án : C
Sử dụng giản đồ véctơ
Theo đầu bài, ta có:
\(\begin{array}{l}{R^2} = \dfrac{L}{C} = \omega L\dfrac{1}{{\omega C}} = {Z_L}{Z_C}\\ \to \dfrac{{{Z_L}}}{R}\dfrac{{\left( { - {Z_L}} \right)}}{R} = - 1\\ \to \tan {\varphi _{RL}}\tan {\varphi _{RC}} = - 1\\ \Rightarrow {u_{RL}} \bot {u_{RC}}\end{array}\)
Vẽ giản đồ véctơ, ta được:
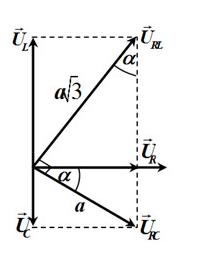
Từ giản đồ véctơ, ta có:
\(\begin{array}{l}\tan \alpha = \dfrac{{{U_{RC}}}}{{{U_{RL}}}} = \dfrac{a}{{a\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }} \to \alpha = {30^0}\\\left\{ \begin{array}{l}{U_R} = ac{\rm{os}}\alpha = \dfrac{{a\sqrt 3 }}{2}\\{U_C}{\rm{ = asin}}\alpha = \dfrac{a}{2}\\{U_L} = a\sqrt 3 {\rm{cos}}\alpha = \dfrac{{3a}}{2}\end{array} \right. \\\to c{\rm{os}}\varphi {\rm{ = }}\dfrac{{{U_R}}}{U} = \dfrac{{{U_R}}}{{\sqrt {{U_R}^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} }} = \sqrt {\dfrac{3}{7}} \end{array}\)
Cho đoạn mạch RLC mắc nối tiếp , cuộn dây cảm thuần, điện trở R thay đổi được. Đặt hai đầu đoạn mạch một điện áp xoay chiều có điện áp hiệu dụng là 200V. Khi R = R1 và R = R2 thì mạch có cùng công suất. Biết \({R_1} + {\rm{ }}{R_2} = {\rm{ }}100\Omega .\) Khi R = R1 công suất của mạch là:
-
A.
400 W
-
B.
220 W
-
C.
440W
-
D.
880 W
Đáp án : A
Vận dụng biểu thức khi R1 ; R2 có cùng P:
\(\left\{ \begin{array}{l}{R_1} + {R_2} = \frac{{{U^2}}}{P}\\{R_1}{R_2} = {\left( {{Z_L} - {Z_C}} \right)^2} = {R_{Pm{\rm{ax}}}}^2\end{array} \right.\)
Vì có 2 giá trị R1, R2 cho cùng công suất
Nên theo vi- et ta có:
\({R_1} + {\text{ }}{R_2} = {\text{ }}U^2/P\)
\( \to P = \dfrac{{{\text{ }}U^2}}{{\left( {{\text{ }}{R_1} + {\text{ }}{R_2}} \right)}} = {\text{ }}400W\)
Một chiếc đèn neon đặt dưới một điện áp xoay chiều $119V-50Hz$. Nó chỉ sáng lên khi điện áp tức thời giữa hai đầu bóng đèn có trị tuyệt đối lớn hơn $84V$. Thời gian bóng đèn sáng trong một chu kì là bao nhiêu?
-
A.
\(\Delta t = 0,0100s\)
-
B.
\(\Delta t = 0,0133s\)
-
C.
\(\Delta t = 0,0200s\)
-
D.
\(\Delta t = 0,0233s\)
Đáp án : B
+ Nhận biết cách ghi các thông số trên đèn
+ Sử dụng vòng tròn lượng giác
+ Vận dụng biểu thức tính tần số góc:
$\omega = 2\pi f$
+ Vận dụng biểu thức:
\(\Delta \varphi = \omega \Delta t\)
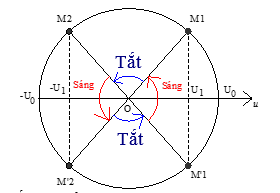
Ta có:
+ Hiệu điện thế cực đại:
${U_0} = 119\sqrt 2 (V)$
+ Tần số góc:
$\omega = 2\pi f = 2\pi .50 = 100\pi (ra{\text{d}}/s)$
+ Vẽ trên vòng tròn lượng giác, ta được:
Biết đèn chỉ sáng lên khi u ≥ U1
Ta có:
+ $c{\text{os}}\Delta \varphi = \frac{{{U_1}}}{{{U_0}}} = \frac{{84}}{{119\sqrt 2 }} \approx 0,5 \to \Delta \varphi = \frac{\pi }{3}$
Thời gian đèn sáng trong 1 chu kì:
$\Delta t = \frac{{4\Delta \varphi }}{\omega } = \frac{{4\frac{\pi }{3}}}{{100\pi }} = \frac{1}{{75}}s \approx 0,01333(s)$
Người ta cần truyền một công suất điện một pha 100kW dưới một hiệu điện thế hiệu dụng 5kV đi xa. Mạch điện có hệ số công suất \(cos\varphi = {\rm{ }}0,8\Omega \) . Muốn cho tỷ lệ năng lượng mất trên đường dây không quá 10% thì điện trở của đường dây phải có giá trị trong khoảng nào?
-
A.
10Ω≤ R ≤12Ω
-
B.
R ≤ 14 Ω
-
C.
R ≤16 Ω
-
D.
16Ω ≤ R ≤ 18 Ω
Đáp án : C
Vận dụng công thức tính công suất hao phí: \({P_{hp}} = \Delta P = \dfrac{{{P^2}}}{{{{\left( {U\cos \varphi } \right)}^2}}}R\)
Muốn cho tỉ lệ năng lượng mất trên đường dây không quá 10 thì công suất hao phí trên đường dây không quá công suất cần truyền đi.
Php ≤ 10% P
lại có :
\(\begin{array}{l}{P_{hp}} = {\left( {\dfrac{P}{{U\cos \varphi }}} \right)^2}.R \Leftrightarrow {P_{hp}} = {\left( {\dfrac{P}{{U\cos \varphi }}} \right)^2}.R \le 10\% .P\\ \Leftrightarrow R \le 10\% = 10\% .\dfrac{{{{\left( {U.\cos \varphi } \right)}^2}}}{P} = \dfrac{{{{\left( {{{5.10}^3}.0,8} \right)}^2}}}{{{{100.10}^3}}} = 16\Omega \end{array}\)
Cho một đoạn mạch điện xoay chiều chỉ có cuộn cảm thuần. Tại thời điểm t1 điện áp và dòng điện qua cuộn cảm có giá trị lần lượt là 25 V; 0,3 A. Tại thời điểm t2 điện áp và dòng điện qua cuộn cảm có giá trị lần lượt là 15 V; 0,5 A. Cảm kháng của mạch có giá trị là:
-
A.
30 Ω.
-
B.
50 Ω.
-
C.
40 Ω.
-
D.
100 Ω.
Đáp án : B
+ Áp dụng hệ thức: \({\left( {\dfrac{u}{{{U_0}}}} \right)^2} + {\left( {\dfrac{i}{I}} \right)^2} = 1\)
+ Áp dụng công thức tính cảm kháng:
\({Z_L} = \dfrac{{{U_0}}}{{{I_0}}}\)
Ta có:
Mạch chỉ có cuộn cảm nên điện áp nhanh pha hơn dòng điện góc π/2.
Khi đó ta có: \({\left( {\dfrac{u}{{{U_0}}}} \right)^2} + {\left( {\dfrac{i}{I}} \right)^2} = 1\)
Tại thời điểm t1:
\({\left( {\dfrac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{i{}_1}}{{{I_0}}}} \right)^2} = 1\)
Tại thời điểm t2:
\({\left( {\dfrac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{i{}_2}}{{{I_0}}}} \right)^2} = 1\)
Từ đó ta được:
\({\left( {\dfrac{{{u_1}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{i{}_1}}{{{I_0}}}} \right)^2} = {\left( {\dfrac{{{u_2}}}{{{U_0}}}} \right)^2} + {\left( {\dfrac{{i{}_2}}{{{I_0}}}} \right)^2} \to \dfrac{{u_1^2 - u_2^2}}{{U_0^2}} = \dfrac{{i_2^2 - i_1^2}}{{I_0^2}} \to \dfrac{{{U_0}}}{{{I_0}}} = \sqrt {\dfrac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \)
Mặt khác, ta có:
\({Z_L} = \dfrac{{{U_0}}}{{{I_0}}} = \sqrt {\dfrac{{u_1^2 - u_2^2}}{{i_2^2 - i_1^2}}} \) .
Thay số ta được ZL = 50 W
Xét một mạch điện gồm một động cơ điện ghép nối tiếp với một tụ điện. Đặt vào hai đầu mạch một điện áp xoay chiều có giá trị hiệu dụng U= 100V thì mạch có hệ số công suất là 0,9. Lúc này động cơ hoạt động bình thường với hiệu suất 80% và hệ số công suất 0,75. Biết điện trở trong của động cơ là 10Ω. Điện áp hiệu dụng hai đầu động cơ và cường độ dòng điện hiệu dụng qua động cơ lần lượt:
-
A.
120V,6A
-
B.
125V,6A
-
C.
120V,1,8A
-
D.
125V, 1,8A
Đáp án : C
Vận dụng biểu thức tính công suất: \(P = UIc{\rm{os}}\varphi \)
vì khi động cơ hoạt động bình thường thì \(H{\rm{ }} = {\rm{ }}80{\rm{ }}\% \)
\(\begin{array}{l} \Rightarrow {P_{hp}} = 0,2P\\ \Rightarrow {I^2}R = 0,2UIcos\varphi \\ \Rightarrow I.R = 0,2Ucos\varphi \\ \Leftrightarrow 10I = 0,2.100.0,9\\ \Rightarrow I = 1,8A\end{array}\)
Lại có \(I{'^2}R{\rm{ }} = 0,2U'Icos\varphi '\)
Vì I không đổi, nên khi động cơ hoạt động bình thường với hiệu suất \(80\% \) và hệ số công suất \(0,75\)
\(I = I' = 1,8A\)
\(\begin{array}{l}{P_{hp}} = 0,2P'\\ \Leftrightarrow I{'^2}R = 0,2U'I'cos\varphi '\\ \Leftrightarrow I'R = 0,2U'cos\varphi '\\ \Leftrightarrow 1,8.10 = 0,2.U'.0,75\\ \Rightarrow U' = 120V\end{array}\)
Cho đoạn mạch AB gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp; trong đó R và C không đổi, còn L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = U\sqrt 2 {\rm{cos(}}\omega {\rm{t + }}{\varphi _u})\) (với \(U,\omega \) không đổi). Điều chỉnh L tới giá trị L1 thì hiệu điện thế hiệu dụng hai đầu cuộn cảm đạt giá trị cực đại và bằng ULmax. Gọi UCmax là giá trị hiệu điện thế hiệu dụng cực đại ở hai đầu tụ điện. Cho biết \({U_{L\max }} = \sqrt 5 {U_{Rm{\rm{ax}}}}\) . Hệ thức nào sau đây là đúng?
-
A.
\(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{2}{{\sqrt 5 }}\)
-
B.
\(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{{\sqrt 5 }}{2}\)
-
C.
\(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{1}{{\sqrt 5 }}\)
-
D.
\(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{1}{{2\sqrt 5 }}\)
Đáp án : A
- L biến thiên để URmax, UCmax<=> cộng hưởng điện
Khi đó: \(\left\{ \begin{array}{l}{U_{{R_{{\rm{max}}}}}} = U\\{U_{{C_{{\rm{max}}}}}} = \frac{U}{R}{Z_C}\end{array} \right.\)
- L biến thiên để ULmax
Khi đó: \({U_{{L_{{\rm{max}}}}}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R}\)
Theo đề bài, ta có:
\(\begin{array}{l}{U_{{L_{{\rm{max}}}}}} = \sqrt 5 {U_{{R_{{\rm{max}}}}}} = \sqrt 5 U\\ \to \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{R} = \sqrt 5 U \to \sqrt {{R^2} + Z_C^2} = \sqrt 5 R\\ \to Z_C^2 = 4{R^2} \to {Z_C} = 2R\end{array}\)
=> Tỉ số: \(\dfrac{{{U_{{C_{{\rm{max}}}}}}}}{{{U_{{L_{{\rm{max}}}}}}}} = \dfrac{{\dfrac{U}{R}{Z_C}}}{{\sqrt 5 U}} = \dfrac{{{Z_C}}}{{\sqrt 5 R}} = \dfrac{{2R}}{{\sqrt 5 R}} = \dfrac{2}{{\sqrt 5 }}\)
Một mạch điện xoay chiều có u là điện áp tức thời ở hai đầu đoạn mạch và i là cường độ tức thời qua mạch. Chọn phát biểu sai.
-
A.
u và i luôn biến thiên cùng tần số
-
B.
Mạch chỉ có điện trở u và i vuông pha
-
C.
Mạch chỉ có cuộn cảm thuần u sớm pha hơn i một góc \(\frac{\pi }{2}\)
-
D.
Mạch chỉ có tụ điện u trễ pha hơn i một góc \(\frac{\pi }{2}\)
Đáp án : B
A, C, D – đúng
B – sai vì: Mạch chỉ có điện trở thì u và i cùng pha với nhau
Khái niệm cường độ dòng điện hiệu dụng được xây dựng dựa trên tác dụng nào của dòng điện?
-
A.
Tác dụng hóa học của dòng điện.
-
B.
Tác dụng nhiệt của dòng điện.
-
C.
Tác dụng từ của dòng điện.
-
D.
Tác dụng phát quang của dòng điện.
Đáp án : B
Định nghĩa về cường độ dòng điện hiệu dụng như sau: Cường độ dòng điện hiệu dụng của dòng điện xoay chiều là cường độ dòng điện một chiều không đổi khi cho chúng lần lượt đi qua cùng một điện trở trong cùng một khoảng thời gian thì chúng toả ra những nhiệt lượng bằng nhau.
Vậy khái niệm cường độ dòng điện hiệu dụng được xây dựng dựa vào tác dụng nhiệt của dòng điện.
Trường hợp nào sau đây có thể dùng dòng điện xoay chiều để sử dụng?
-
A.
Mạ điện
-
B.
Đúc điện
-
C.
Đèn điện dây tóc
-
D.
Điều chế kim loại bằng điện phân
Đáp án : C
Vận dụng lí thuyết và ứng dụng của dòng điện xoay chiều
Ta có:
+ Mạ điện, đúc điện và điều chế kim loại bằng điện phân chỉ có thể dùng dòng điện một chiều
+ Bếp điện, đèn dây tóc có thể dùng đồng thời cả hai loại dòng điện xoay chiều và dòng điện không đổi
Đoạn mạch RLC nối tiếp \(R = 40\Omega \); \(L = \dfrac{{0,4}}{\pi }(H)\)và \(C = \dfrac{{{{10}^{ - 3}}}}{\pi }(F)\). Cho tần số dòng điện là \(50{\rm{ }}Hz\) và điện áp hiệu dụng ở hai đầu R là \(40{\rm{ }}V\). Điện áp ở hai đầu đoạn mạch là:
-
A.
100 V
-
B.
150 V
-
C.
200 V
-
D.
50 V
Đáp án : D
+ Vận dụng biêu thức tính hiệu điện thế: \(U = I.Z\)
+ Vận dụng biểu thức tính cảm kháng, dung kháng: \({Z_L} = \omega L;{Z_C} = \dfrac{1}{{\omega C}}\)
+ Vận dụng biểu thức tính hiệu điện thế hiệu dụng toàn mạch: \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} \)
Ta có:
Cường độ dòng điện trong mạch: \(I = \dfrac{{{U_R}}}{R} = \dfrac{{40}}{{40}} = 1(A)\)
Cảm kháng: \({Z_L} = \omega L = 2\pi fL = 2\pi .50.\dfrac{{0,4}}{\pi } = 40\Omega \)
Hiệu điện thế hiệu dụng hai đầu cuộn cảm: \({U_L} = I.{Z_L} = 1.40 = 40(V)\)
Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 3}}}}{\pi }}} = 10\Omega \)
Hiệu điện thế hiệu dụng hai đầu tụ điện: \({U_C} = I.{Z_C} = 1.10 = 10(V)\)
Hiệu điện thế hiệu dụng toàn mạch: \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = \sqrt {{{40}^2} + {{\left( {40 - 10} \right)}^2}} = 50(V)\)
Biết cường độ dòng điện qua đoạn mạch chỉ có điện trở có biểu thức \(i = {I_0}cos\left( {\omega t} \right)A\). Biểu thức điện áp đặt vào hai đầu đoạn mạch là:
-
A.
\(u = {I_0}Rcos\left( {\omega t + \dfrac{\pi }{2}} \right)V\)
-
B.
\(u = \dfrac{{{I_0}}}{R}cos\left( {\omega t} \right)V\)
-
C.
\(u = \dfrac{{{I_0}}}{R}cos\left( {\omega t + \dfrac{\pi }{2}} \right)V\)
-
D.
\(u = {I_0}Rcos\left( {\omega t} \right)V\)
Đáp án : D
+ Trong mạch chỉ có R: u và i cùng pha với nhau
+ Sử dụng biểu thức tính hiệu điện thế cực đại
Ta có:
+ \({u_R}\) luôn luôn cùng pha với \(i\)
+ Hiệu điện thế cực đại: \({U_0} = {I_0}R\)
=> Biểu thức điện áp đặt vào hai đầu đoạn mạch: \(u = {I_0}Rcos\left( {\omega t} \right)V\)
Đồ thị cường độ dòng điện như hình vẽ

Cường độ dòng điện tức thời có biểu thức
-
A.
\(i = 4c{\rm{os}}\left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
-
B.
\(i = 4c{\rm{os}}\left( {50\pi t} \right)A\)
-
C.
\(i = 4c{\rm{os}}\left( {100\pi t} \right)A\)
-
D.
\(i = 4c{\rm{os}}\left( {50\pi t + \dfrac{\pi }{2}} \right)A\)
Đáp án : B
Đọc đồ thị cường độ dòng điện theo thời gian
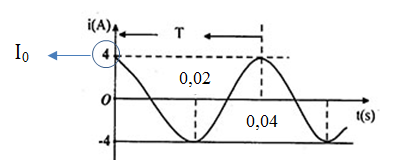
Từ đồ thị ta có:
+ Chu kì: \(T = 0,04{\rm{s}} \to \omega {\rm{ = }}\dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,04}} = 50\pi (ra{\rm{d}}/s)\)
+ Cường độ dòng điện cực đại: \({I_0} = 4(A)\)
+ Tại t = 0: \(i = 4 \leftrightarrow {I_0}{\rm{cos}}\varphi {\rm{ = 4}} \to c{\rm{os}}\varphi {\rm{ = 1}} \to \varphi {\rm{ = 0}}\)
=> Biểu thức cường độ dòng điện tức thời: \(i = 4c{\rm{os}}\left( {50\pi t} \right)A\)
Cuộn dây có điện trở thuần \(R = 50\Omega \) và độ tự cảm L mắc vào điện áp xoay chiều \(U = 110{\rm{ }}V\) có tần số \(f = 60Hz\). Cho biết công suất của mạch điện là \(100W\). Giá trị của L là:
-
A.
\(0,637H\)
-
B.
\(0,318H\)
-
C.
\(0,5H\)
-
D.
\(0,158H\)
Đáp án : D
+ Vận dụng biểu thức tính công suất: \(P = \dfrac{{{U^2}}}{{{Z^2}}}R\)
+ Vận dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)
+ Áp dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
Ta có:
+ Công suất tiêu thụ của mạch điện: \(P = \dfrac{{{U^2}}}{{{Z^2}}}R\)
+ Do mạch là cuộn dây có điện trở thuần và độ tự cảm L => tổng trở của mạch: \(Z = \sqrt {{R^2} + {Z_L}^2} \)
\( \to P = \dfrac{{{U^2}}}{{{R^2} + Z_L^2}}R \leftrightarrow 100 = \dfrac{{{{110}^2}}}{{{{50}^2} + {Z_L}^2}}50 \to {Z_L} = 59,6\Omega \)
+ Mặt khác, ta có: \({Z_L} = \omega L = 2\pi fL \to L = \dfrac{{{Z_L}}}{{2\pi f}} = \dfrac{{59,6}}{{2\pi .60}} = 0,158(H)\)
Mạch điện nối tiếp gồm điện trở \(R\), cuộn dây thuần cảm có độ tự cảm \(L\) và tụ điện có điện dung \(C\) thay đổi được . Điện áp hai đầu là \(U\) ổn định, tần số \(f\). Thay đổi \(C\) để \({U_{Cmax}}\). Chọn hệ thức sai?
-
A.
\(U_{Cm{\rm{ax}}}^2 = {U^2} + U_R^2 + U_L^2\)
-
B.
\(U_{Cm{\rm{ax}}}^2 = {U^2} + U_{RL}^2\)
-
C.
\({U_{{C_{max}}}}.{U_R} = U.{U_{RL}}\)
-
D.
\(\dfrac{1}{{U_{{C_{max}}}^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\)
Đáp án : D
Ta có C thay đổi để UC max, khi đó:\({U_{Cm{\rm{ax}}}} = \dfrac{{U_R^2 + U_L^2}}{{{U_L}}} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{R}\)
\(\left\{ \begin{array}{l}{U_{RL}} \bot {U_{AB}}\\U_{C\max }^2 = {U^2} + U_{RL}^2 = {U^2} + U_R^2 + U_L^2\\U_{C\max }^{}.{U_R} = U.{U_{RL}}\\\dfrac{1}{{U_R^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\end{array} \right.\)
=> Các phương án:
+ A, B, C – đúng
+ D – sai vì: \(\dfrac{1}{{U_R^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\)
Trên đoạn mạch xoay chiều không phân nhánh có 4 điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có cuộn cảm thuần, giữa hai điểm M và N chỉ có điện trở thuần, giữa hai điểm N và B chỉ có tụ điện. Điện áp hiệu dụng giữa hai điểm A và N là \(400{\rm{ }}V\) và điện áp hiệu dụng giữa hai điểm M và B là \(300{\rm{ }}V\). Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau \({90^0}\). Biết cường độ dòng điện hiệu dụng trong mạch có giá trị \(3\sqrt 2 A\). Giá trị của điện trở R là:
-
A.
\(80\Omega \)
-
B.
\(25\sqrt 2 \Omega \)
-
C.
\(30\sqrt 2 \Omega \)
-
D.
\(40\sqrt 2 \Omega \)
Đáp án : D
+ Sử dụng giản đồ véctơ và các hệ thức trong tam giác
+ Sử dụng biểu thức: \(R = \dfrac{{{U_R}}}{I}\)
Vẽ lại mạch điện và vẽ giản đồ véctơ, ta được:
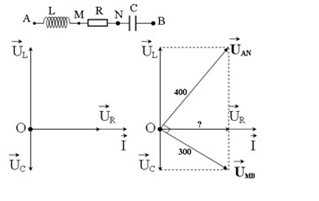
Từ giản đồ véctơ, ta có: \(\dfrac{1}{{U_R^2}} = \dfrac{1}{{U_{AN}^2}} + \dfrac{1}{{U_{MB}^2}} = \dfrac{1}{{{{300}^2}}} + \dfrac{1}{{{{400}^2}}} \to {U_R} = 240V\)
=> Điện trở \(R = \dfrac{{{U_R}}}{I} = \dfrac{{240}}{{3\sqrt 2 }} = 40\sqrt 2 \Omega \)
Một đoạn mạch điện gồm một cuộn dây thuần cảm có độ tự cảm \(L = 1/π (H)\) và điện trở thuần \(R = 100 Ω\). Đặt vào hai đầu mạch một điện áp xoay chiều \(u = 200cos(100πt + π/4) V\) thì biểu thức nào sau đây là của điện áp hai đầu cuộn cảm thuần ?
-
A.
\({u_L} = 100\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{4}} \right)V\)
-
B.
\({u_L} = 100cos\left( {100\pi t + \dfrac{\pi }{2}} \right)V\)
-
C.
\({u_L} = 100\sqrt 2 cos\left( {100\pi t - \dfrac{\pi }{2}} \right)V\)
-
D.
\({u_L} = 100\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{2}} \right)V\)
Đáp án : D
Sử dụng máy tính casio
Cài đặt máy tính ở chế độ radian SHIFT MODE 4
Bấm máy tính MODE 2 (Chọn CMPLX)
Cảm kháng của cuộn dây ZL = ωL = 100 Ω
Tổng trở của đoạn mạch \(\overline Z = R + {Z_L}i = 100 + 100i\)
Cường độ dòng điện trong mạch \(\overline I = \displaystyle{{\overline U } \over {\overline Z }} = {{200\angle \displaystyle{\pi \over 4}} \over {100 + 100i}}\) SHIFT 2 3 =
Ta đọc kết quả \(\overline I = \sqrt 2 \angle 0\)
Điện áp hiệu dụng hai đầu cuộn cảm là \(\overline {{U_L}} = \overline I .\overline {{Z_L}} = \left( {\sqrt 2 \angle 0} \right).100i\) SHIFT 2 3 =
Ta đọc kết quả \(\overline {{U_L}} = 100\sqrt 2 \angle \displaystyle{\pi \over 2}\)
Vậy biểu thức điện áp hai đầu cuộn cảm là \(u_L=100\sqrt 2 \cos \left( {100\pi t + \displaystyle{\pi \over 2}} \right)V\)
Cuộn sơ cấp và cuộn thứ cấp của một máy biến áp lí tưởng có số vòng dây lần lượt là N1 và N2. Đặt điện áp xoay chiều có giá trị hiệu dụng U1 vào hai đầu cuộn sơ cấp thì điện áp hiệu dụng giữa hai đầu cuộn thứ cấp để hở là U2. Hệ thức đúng là:
-
A.
\(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_2}}}{{{N_1}}}\)
-
B.
\(\dfrac{{{U_1}}}{{{N_1}}} = {U_2}{N_2}\)
-
C.
\({U_1}{U_2} = {N_1}{N_2}\).
-
D.
\(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}}\)
Đáp án : D
Sử dụng biểu thức của máy biến áp lí tưởng: \(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}}\)
Ta có: \(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}}\)
=> Phương án D đúng
Đặt điện áp xoay chiều \(u = {U_0}\cos \omega t\) vào hai đầu đoạn mạch chỉ có điện trở thuần. Gọi U là điện áp hiệu dụng giữa hai đầu đoạn mạch; i, I0 và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường độ dòng điện trong đoạn mạch. Hệ thức nào sau đây sai?
-
A.
\(\dfrac{U}{{{U_0}}} - \dfrac{I}{{{I_0}}} = 0\)
-
B.
\(\dfrac{U}{{{U_0}}} + \dfrac{I}{{{I_0}}} = \sqrt 2 \)
-
C.
\(\dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1\)
-
D.
\(\dfrac{u}{U} - \dfrac{i}{I} = 0\)
Đáp án : C
Mạch chỉ có điện trở thuần: \(i\) cùng pha với \(u\)
Hệ thức sai là: \(\dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1\)
vì u và i cùng pha với nhau, ta có:
\(\left\{ \begin{array}{l}u = {U_0}cos\left( {\omega t + \varphi } \right)\\i = {I_0}cos\left( {\omega t + \varphi } \right)\end{array} \right. \\\Rightarrow \dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 2co{s^2}\left( {\omega t + \varphi } \right)\)
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận