Đề kiểm tra 15 phút chương 3: Dòng điện xoay chiều - Đề số 01

Làm đề thi

Đề bài

Câu 1 :

Đoạn mạch RLC nối tiếp. Biết điện áp tức thời ở hai đầu đoạn mạch sớm pha hơn cường độ dòng điện tức thời i chạy qua mạch 45⁰. Chọn kết luận đúng:

A.

$R{\rm{ }} = {\rm{ }}{Z_L}-{\rm{ }}{Z_C}$
B.

$R{\rm{ }} = {\rm{ }}{Z_L} > {\rm{ }}{Z_{C}}$
C.

$R{\rm{ }} = {\rm{ }}{Z_C} - {\rm{ }}{Z_L}$
D.

$R{\rm{ }} = {\rm{ }}{Z_C} > {\rm{ }}{Z_L}$

Câu 2 :

Một cuộn dây thuần cảm có độ tự cảm L được mắc vào điện áp xoay chiều u có tần số f. Chọn phát biểu đúng:

A.

Cường độ dòng điện biến thiên điều hòa cùng pha với điện áp u.
B.

Cường độ hiệu dụng qua mạch tỉ lệ nghịch với f.
C.

Cường độ dòng điện qua mạch tỉ lệ thuận với L.
D.

Cường độ dòng điện biến thiên điều hòa với tần số f’ = 2f

Câu 3 :

Đoạn mạch RLC nối tiếp có hệ số công suất lớn nhất khi?

A.

${Z_L} = {Z_C}$
B.

$T = \pi \sqrt {LC} $
C.

$Z = 2R$
D.

$U = {U_L} = {U_C}$

Câu 4 :

Một khung dây dân có diện tích $S = 100c{m^2}$ gồm $100$ vòng dây quay đều với vận tốc $n$ vòng/phút trong một từ trường đều $\vec B$ vuông góc trục quay $\Delta $ và có độ lớn $B{\rm{ }} = {\rm{ }}0,02{\rm{ }}T$. Từ thông cực đại gửi qua khung là:

A.

$200{\rm{ }}Wb$
B.

$0,02Wb$
C.

$2Wb$
D.

$0,2Wb$

Câu 5 :

Chọn phát biểu đúng

A.

Dòng điện xoay chiều qua điện trở thuần R chỉ có tác dụng nhiệt.
B.

Điện áp ở hai đầu đoạn mạch chỉ có điện trở thuần biến thiên điều hòa cùng tần số, khác pha với cường độ dòng điện.
C.

Cường độ dòng điện qua đoạn mạch chỉ có điện trở thuần biến thiên điều hòa vuông pha với điện áp.
D.

Nhiệt lượng tỏa ra ở điện trở thuần tỉ lệ với cường độ hiệu dụng qua nó.

Câu 6 :

Cho một khung dây dẫn phẳng có diện tích S quay đều với tốc độ góc quanh một trục vuông góc với các đường cảm ứng từ $\vec B$. Trong khung dây sẽ xuất hiện:

A.

Hiện tượng tự cảm.
B.

Suất điện động cảm ứng.
C.

Dòng điện một chiều.
D.

Suất điện động tự cảm.

Câu 7 :

Dòng điện xoay chiều qua một đoạn mạch có tần số dao động là $f$. Mỗi giây dòng điện đổi chiều bao nhiêu lần?

A.

$0,5f$
B.

$f$
C.

$2f$
D.

$4f$

Câu 8 :

Mạch điện xoay chiều có điện trở R, cảm kháng Z_L và dung kháng Z_C. Công thức tính góc lệch pha $\varphi $ giữa u và i là:

A.

$\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}$
B.

$\tan \varphi = \dfrac{{R - {Z_C}}}{{{Z_L}}}$
C.

$\tan \varphi = \dfrac{{{Z_L} + {Z_C}}}{R}$
D.

$\tan \varphi = \dfrac{R}{Z}$

Câu 9 :

Tại thời điểm t, điện áp $u = 200\sqrt 2 {\rm{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)$ (trong đó u tính bằng V, t tính bằng s) có giá trị $100\sqrt 2 $ và đang tăng. Sau thời điểm đó $\dfrac{7}{{600}}s$, điện áp này có giá trị là:

A.

$ - 100\sqrt 6 V$
B.

$100\sqrt 6 V$
C.

$ - 100\sqrt 2 V$
D.

$200V$

Câu 10 :

Mạch RLC nối tiếp có $R = 100\Omega $, L và $C = \dfrac{{200}}{\pi }(\mu F)$. Cho biết $f = 50 Hz$ và dòng điện qua mạch chậm pha $45^0$. Giá trị đúng của $L$ là:

A.

$\dfrac{{1,5}}{\pi }H$
B.

$\dfrac{1}{\pi }H$
C.

$\dfrac{2}{\pi }H$
D.

$\dfrac{{0,5}}{\pi }H$

Câu 11 :

Biểu thức cường độ dòng điện qua mạch chỉ có điện trở $R$có dạng $i = 2\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{2}} \right)A$. Biết điện trở có giá trị $R = 10\Omega $, biểu thức điện áp của mạch là:

A.

$u = 20cos(100\pi t + \dfrac{\pi }{2}){\rm{ }}V$
B.

$u = 20\sqrt 2 cos(100\pi t + \dfrac{\pi }{2}){\rm{ }}V$
C.

$u = 20cos(100\pi t){\rm{ }}V$
D.

$u = 20\sqrt 2 cos(100\pi t + {\rm{ }}\pi ){\rm{ }}V$

Câu 12 :

Mạch điện xoay chiều RLC nối tiếp. Hai đầu đoạn mạch có một điện áp xoay chiều có tần số và điện áp hiệu dụng không đổi. Dùng vôn kế có điện trở rất lớn, lần lượt đo điện áp ở hai đầu đoạn mạch, hai đầu tụ điện và hai đầu cuộn dây thì số chỉ của vôn kế tương ứng là U, U_Cvà U_L. Biế U = U_C = 2U_L. Hệ số công suất của mạch là:

A.

$\cos \varphi = 0,5$
B.

$\cos \varphi = \sqrt 3 /2$
C.

$\cos \varphi = \sqrt 2 /2$
D.

$\cos \varphi = 1$

Lời giải và đáp án

Câu 1 :

A.

$R{\rm{ }} = {\rm{ }}{Z_L}-{\rm{ }}{Z_C}$
B.

$R{\rm{ }} = {\rm{ }}{Z_L} > {\rm{ }}{Z_{C}}$
C.

$R{\rm{ }} = {\rm{ }}{Z_C} - {\rm{ }}{Z_L}$
D.

$R{\rm{ }} = {\rm{ }}{Z_C} > {\rm{ }}{Z_L}$

Đáp án : A

Phương pháp giải :

Vận dụng biểu thức tính độ lệch pha giữa u và i :

$\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}$

Lời giải chi tiết :

Ta có :

+ u nhanh pha hơn i một góc 45⁰

+ độ lệch pha giữa u và i được xác định bởi biểu thức :

$\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}$

$\begin{array}{l} \to \tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \tan \dfrac{\pi }{4}\\ \to {Z_L} - {Z_C} = R\end{array}$

Câu 2 :

Một cuộn dây thuần cảm có độ tự cảm L được mắc vào điện áp xoay chiều u có tần số f. Chọn phát biểu đúng:

A.

Cường độ dòng điện biến thiên điều hòa cùng pha với điện áp u.
B.

Cường độ hiệu dụng qua mạch tỉ lệ nghịch với f.
C.

Cường độ dòng điện qua mạch tỉ lệ thuận với L.
D.

Cường độ dòng điện biến thiên điều hòa với tần số f’ = 2f

Đáp án : B

Lời giải chi tiết :

A- sai vì: Cường độ dòng điện trong mạch chỉ có L trễ pha hơn điện áp u

B- đúng

C- sai vì:

$I = \frac{U}{{{Z_L}}} = \frac{U}{{\omega L}} = \frac{U}{{2\pi fL}}$

=> cường độ dòng điện tỉ lệ nghịch với L và f

D- sai vì cường độ dòng điện biến thiên điều hòa với tần số f

Câu 3 :

Đoạn mạch RLC nối tiếp có hệ số công suất lớn nhất khi?

A.

${Z_L} = {Z_C}$
B.

$T = \pi \sqrt {LC} $
C.

$Z = 2R$
D.

$U = {U_L} = {U_C}$

Đáp án : A

Phương pháp giải :

Vận dụng các biểu thức khi mạch RLC mắc nối tiếp có hệ số công suất lớn nhất

Lời giải chi tiết :

Ta có, mạch RLC mắc nối tiếp có hệ số công suất lớn nhất khi: ${Z_L} = {Z_C}$

Khi đó, ta có:

+ $\omega = \dfrac{1}{{\sqrt {LC} }} \to T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {LC} $

+ Công suất cực đại: ${P_{{\rm{max}}}} = UI$

+ Tổng trở khi đó: $Z = R$

+ $U = {U_R}$

=> Các phương án:

A – đúng

B, C, D - sai

Câu 4 :

A.

$200{\rm{ }}Wb$
B.

$0,02Wb$
C.

$2Wb$
D.

$0,2Wb$

Đáp án : B

Phương pháp giải :

Áp dụng biểu thức xác định từ thông cực đại qua khung: ${\Phi _0} = NBS$

Lời giải chi tiết :

Ta có từ thông cực đại qua khung:

${\phi _0} = NBS = 100.0,02.({100.10^{ - 4}}) = 0,02Wb$

Câu 5 :

Chọn phát biểu đúng

A.

Dòng điện xoay chiều qua điện trở thuần R chỉ có tác dụng nhiệt.
B.

Điện áp ở hai đầu đoạn mạch chỉ có điện trở thuần biến thiên điều hòa cùng tần số, khác pha với cường độ dòng điện.
C.

Cường độ dòng điện qua đoạn mạch chỉ có điện trở thuần biến thiên điều hòa vuông pha với điện áp.
D.

Nhiệt lượng tỏa ra ở điện trở thuần tỉ lệ với cường độ hiệu dụng qua nó.

Đáp án : A

Lời giải chi tiết :

A - đúng

B, C – sai vì: điện áp và cường độ dòng điện trong mạch chỉ có điện trở biến thiên cùng tần số, cùng pha so với nhau.

D - sai vì: Nhiệt lượng tỏa ra ở điện trở thuần tỉ lệ với bình phương cường độ hiệu dụng qua nó

$Q = {I^2}Rt = \frac{{I_0^2Rt}}{2}$

Câu 6 :

A.

Hiện tượng tự cảm.
B.

Suất điện động cảm ứng.
C.

Dòng điện một chiều.
D.

Suất điện động tự cảm.

Đáp án : B

Lời giải chi tiết :

Khi khung dây dẫn phẳng có diện tích S quay đều với tốc độ góc ω quanh một trục vuông góc với các đường cảm ứng từ $\vec B$, theo hiện tượng cảm ứng điện từ trong khung hình thành suất điện động cảm ứng

Câu 7 :

Dòng điện xoay chiều qua một đoạn mạch có tần số dao động là $f$. Mỗi giây dòng điện đổi chiều bao nhiêu lần?

A.

$0,5f$
B.

$f$
C.

$2f$
D.

$4f$

Đáp án : C

Lời giải chi tiết :

Trong mỗi giây: Dòng điện đổi chiều $2f$ lần

Câu 8 :

Mạch điện xoay chiều có điện trở R, cảm kháng Z_L và dung kháng Z_C. Công thức tính góc lệch pha $\varphi $ giữa u và i là:

A.

$\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}$
B.

$\tan \varphi = \dfrac{{R - {Z_C}}}{{{Z_L}}}$
C.

$\tan \varphi = \dfrac{{{Z_L} + {Z_C}}}{R}$
D.

$\tan \varphi = \dfrac{R}{Z}$

Đáp án : A

Lời giải chi tiết :

Công thức tính góc lệch pha giữa u và i là:

$\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}$

Câu 9 :

A.

$ - 100\sqrt 6 V$
B.

$100\sqrt 6 V$
C.

$ - 100\sqrt 2 V$
D.

$200V$

Đáp án : A

Phương pháp giải :

+ Sử dụng biểu thức góc quét trong khoảng thời gian: $\Delta \varphi = \omega \Delta t$

+ Sử dụng vòng tròn lượng giác

Lời giải chi tiết :

Góc quay từ t đến $\dfrac{7}{{600}}s$ : $\Delta \varphi = \omega \Delta t = 100\pi \dfrac{7}{{600}} = \dfrac{{7\pi }}{6}(ra{\rm{d}})$

Xác định các điểm trên vòng tròn lượng giác, ta được:

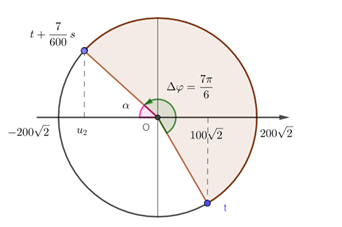
Từ vòng tròn ta có:

Tại thời điểm: $t + \dfrac{7}{{600}}s$: điện áp có giá trị: ${u_2} = - {U_0}cos\alpha $

Ta có: $\alpha = \dfrac{\pi }{6}\left( {rad} \right) \to {u_2} = - {U_0}cos\dfrac{\pi }{6} = - 200\sqrt 2 cos\dfrac{\pi }{6} = - 100\sqrt 6 V$

Câu 10 :

Mạch RLC nối tiếp có $R = 100\Omega $, L và $C = \dfrac{{200}}{\pi }(\mu F)$. Cho biết $f = 50 Hz$ và dòng điện qua mạch chậm pha $45^0$. Giá trị đúng của $L$ là:

A.

$\dfrac{{1,5}}{\pi }H$
B.

$\dfrac{1}{\pi }H$
C.

$\dfrac{2}{\pi }H$
D.

$\dfrac{{0,5}}{\pi }H$

Đáp án : A

Phương pháp giải :

+ Vận dụng biểu thức tính độ lệch pha giữa u và i : $\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}$

+ Vận dụng biểu thức tính cảm kháng, dung kháng: ${Z_L} = \omega L;{Z_C} = \dfrac{1}{{\omega C}}$

Lời giải chi tiết :

Ta có:

+ Dung kháng :

${Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{200}}{\pi }{{.10}^{ - 6}}}} = 50\Omega $

+ Dòng điện qua mạch chậm pha

${45^0} \to \varphi = \dfrac{\pi }{4}$

$\begin{array}{l}\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \tan \dfrac{\pi }{4} \to {Z_L} - {Z_C} = R\\ \to {Z_L} = {Z_C} + R = 50 + 100 = 150\Omega \end{array}$

Mặt khác:

${Z_L} = \omega L \to L = \dfrac{{{Z_L}}}{\omega } = \dfrac{{{Z_L}}}{{2\pi f}} = \dfrac{{150}}{{2\pi .50}} = \dfrac{{1,5}}{\pi }$

Câu 11 :

A.

$u = 20cos(100\pi t + \dfrac{\pi }{2}){\rm{ }}V$
B.

$u = 20\sqrt 2 cos(100\pi t + \dfrac{\pi }{2}){\rm{ }}V$
C.

$u = 20cos(100\pi t){\rm{ }}V$
D.

$u = 20\sqrt 2 cos(100\pi t + {\rm{ }}\pi ){\rm{ }}V$

Đáp án : B

Phương pháp giải :

Ta có: ${u_R} = i.R$ (do ${u_R}$ và $i$ luôn cùng pha với nhau)

Lời giải chi tiết :

+ Ta có $u = {\rm{iR}} = 2\sqrt 2 .10cos\left( {100\pi t + \dfrac{\pi }{2}} \right) = 20\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{2}} \right)V$

Câu 12 :

A.

$\cos \varphi = 0,5$
B.

$\cos \varphi = \sqrt 3 /2$
C.

$\cos \varphi = \sqrt 2 /2$
D.

$\cos \varphi = 1$

Đáp án : B

Phương pháp giải :

+ Áp dụng công thức tính hiệu điện thế hiệu dụng hai đầu đoạn mạch:

$U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} $

+ Áp dụng công thức tính hệ số công suất: ${\rm{cos}}\varphi = \frac{R}{Z}$

Lời giải chi tiết :

Ta có:

+ $\begin{array}{l}U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} \leftrightarrow {U^2} = U_R^2 + {(\frac{U}{2} - U)^2}\\ \to {U_R} = \frac{{\sqrt 3 U}}{2}\end{array}$

+ Hệ số công suất:

${\rm{cos}}\varphi = \frac{R}{Z} = \frac{{{U_R}}}{U} = \frac{{\frac{{\sqrt 3 U}}{2}}}{U} = \frac{{\sqrt 3 }}{2}$

Đề kiểm tra 15 phút chương 3: Dòng điện xoay chiều - Đề số 02

Xem chi tiết

Đề kiểm tra 15 phút chương 3: Dòng điện xoay chiều - Đề số 03

Xem chi tiết

Đề kiểm tra 15 phút chương 4: Dao động và sóng điện từ - Đề số 1

Xem chi tiết

Đề kiểm tra 15 phút chương 4: Dao động và sóng điện từ - Đề số 2

Xem chi tiết

Đề kiểm tra 15 phút chương 4: Dao động và sóng điện từ - Đề số 3

Xem chi tiết

Đề kiểm tra 15 phút chương 5: Sóng ánh sáng - Đề số 1

Xem chi tiết

Đề kiểm tra 15 phút chương 5: Sóng ánh sáng - Đề số 2

Xem chi tiết

Đề kiểm tra 15 phút chương 5: Sóng ánh sáng - Đề số 3

Xem chi tiết

Đề kiểm tra 15 phút chương 6: Lượng tử ánh sáng - Đề số 1

Xem chi tiết

Đề kiểm tra 15 phút chương 6: Lượng tử ánh sáng - Đề số 2

Xem chi tiết

Đề kiểm tra 15 phút chương 6: Lượng tử ánh sáng - Đề số 3

Xem chi tiết

Đề kiểm tra 15 phút chương 7: Hạt nhân nguyên tử - Đề số 1

Xem chi tiết

Đề kiểm tra 15 phút chương 7: Hạt nhân nguyên tử - Đề số 2

Xem chi tiết

Đề kiểm tra 15 phút chương 7: Hạt nhân nguyên tử - Đề số 3

Xem chi tiết

Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - Đề số 03

Xem chi tiết

Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - Đề số 02

Xem chi tiết

Đề kiểm tra 15 phút chương 2: Sóng cơ và sóng âm - Đề số 01

Xem chi tiết

Đề kiểm tra 15 phút chương 1: Dao động cơ - Đề số 04

Xem chi tiết

Đề kiểm tra 15 phút chương 1: Dao động cơ - Đề số 03

Xem chi tiết

Đề kiểm tra 15 phút chương 1: Dao động cơ - Đề số 02

Xem chi tiết

Đề kiểm tra 15 phút chương 1: Dao động cơ - Đề số 01

Xem chi tiết

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục

Bài giải mới nhất

Đề kiểm tra 15 phút chương 3: Dòng điện xoay chiều - Đề số 01

Báo lỗi góp ý