-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Bài 2. Các quy tắc tính đạo hàm
Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao
Tìm đạo hàm của mỗi hàm số sau
Tìm đạo hàm của mỗi hàm số sau
LG a
\(y = {\left( {x - {x^2}} \right)^{32}}\)
Phương pháp giải:
Công thức \(\left( {{u^n}} \right)' = n{u^{n - 1}}u'\)
Lời giải chi tiết:
y' = 32.(x- x2)31.(x - x2)'
= 32(x - x2)31.(1 - 2x)
Vậy \(y' = 32{\left( {x - {x^2}} \right)^{31}}\left( {1 - 2x} \right)\)
LG b
\(y = {1 \over {x\sqrt x }}\)
Phương pháp giải:
Sử dụng công thức \(\left( {\frac{1}{u}} \right)' = \frac{{ - u'}}{{{u^2}}}\)
Lời giải chi tiết:
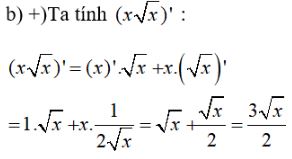
\( \Rightarrow \left( {\frac{1}{{x\sqrt x }}} \right)' = \frac{{ - \left( {x\sqrt x } \right)'}}{{{{\left( {x\sqrt x } \right)}^2}}} \) \(= \frac{{ - \frac{{3\sqrt x }}{2}}}{{{x^2}.x}} = - \frac{3}{{2{x^2}\sqrt x }}\)
\(y' = {{ - 3} \over {2{x^2}\sqrt x }}\)
LG c
\(y = {{1 + x} \over {\sqrt {1 - x} }}\)
Phương pháp giải:
Công thức đạo hàm của một thương: \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\)
Lời giải chi tiết:
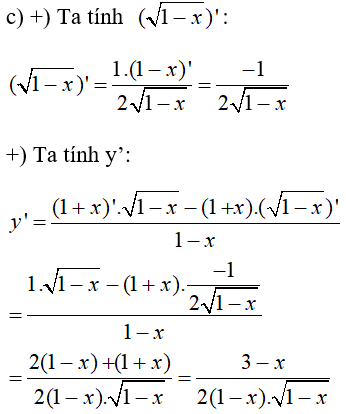
\(y' = {{3 - x} \over {2\sqrt {{{\left( {1 - x} \right)}^3}} }}\)
LG d
\(y = {x \over {\sqrt {{a^2} - {x^2}} }}\) (a là hằng số)
Phương pháp giải:
Công thức đạo hàm của một thương: \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\).
Lời giải chi tiết:
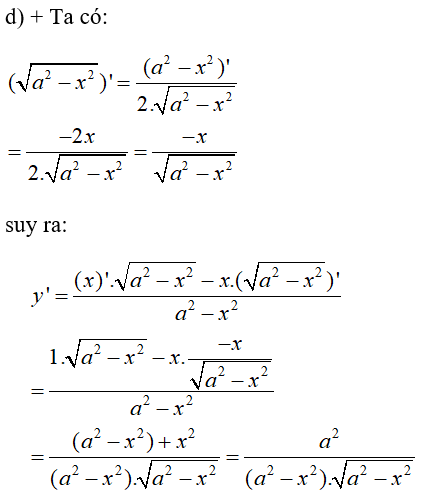
\(\eqalign{ & y' = {{{a^2}} \over {\sqrt {{{\left( {{a^2} - {x^2}} \right)}^3}} }} \cr} \)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 20 trang 204 SGK Đại số và Giải tích 11 Nâng cao
- Câu 21 trang 204 SGK Đại số và Giải tích 11 Nâng cao
- Câu 22 trang 205 SGK Đại số và Giải tích 11 Nâng cao
- Câu 23 trang 205 SGK Đại số và Giải tích 11 Nâng cao
- Câu 24 trang 205 SGK Đại số và Giải tích 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
