Bài 15 trang 30 SGK Hình học 10
Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ.
Đề bài
Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ.
Khẳng định nào sau đây là đúng?
A) \(|\overrightarrow {OA} + \overrightarrow {OB} | = AB\)
B) \(\overrightarrow {OA} - \overrightarrow {OB} \) và \(\overrightarrow {DC}\) cùng hướng
C) \({x_A} = - {x_C}\) và \({y_A} = {y_C}.\)
D) \({x_B} = - {x_C}\) và \({y_C} =- {y_B}.\)
Video hướng dẫn giải
Lời giải chi tiết
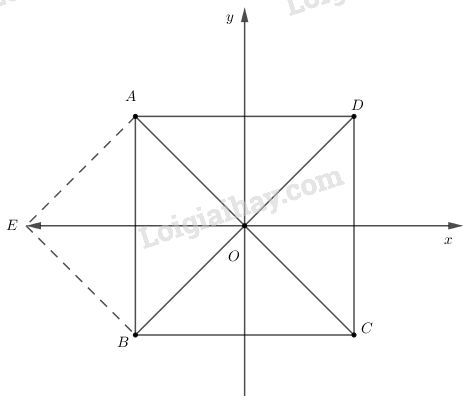
A) Ta có:
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CO} + \overrightarrow {OB} = \overrightarrow {CB} \\
\Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {CB} } \right| = CB = AB
\end{array}\)
A đúng.
B) Vì \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} \)
Mà \(\overrightarrow {BA} \) và \(\overrightarrow {DC} \) ngược hướng nên B) sai
C) Vì \({x_A} = - {x_C},\;\;y{ _A} = - {y_C} \Rightarrow C\) sai.
D) Vì \({x_B} = - {x_C},\;\;{y_B} = {y_C} \Rightarrow D\) sai.
Chọn A.
Cách giải thích khác:
Qua A kẻ \(\overrightarrow {AE} = \overrightarrow {OB} \)\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {AE}\)\( = \overrightarrow {OE} \)
Ta dễ dàng chứng minh được:
\(\overrightarrow {OE} = \overrightarrow {DA} \Rightarrow |\overrightarrow {OA} + \overrightarrow {OB} |= |\overrightarrow {OE} |\)\( =|\overrightarrow {DA} |= |\overrightarrow {BA} | = AB\)
Vậy A) đúng.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 16 trang 31 SGK Hình học 10
- Bài 17 trang 31 SGK Hình học 10
- Bài 18 trang 31 SGK Hình học 10
- Bài 19 trang 31 SGK Hình học 10
- Bài 20 trang 31 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
