Bài 13 trang 30 SGK Hình học 10
Trong mặt phẳng Oxy cho bốn điểm A(-5, -2); B(-5, 3); C(3, 3); D(3, -2).
Đề bài
Trong mặt phẳng \(Oxy\) cho bốn điểm \(A(-5; -2); B(-5; 3); C(3; 3); D(3; -2)\).
Khẳng định nào sau đây là đúng?
A. \(\overrightarrow {AB} ;\overrightarrow {CD} \) cùng hướng
B. Tứ giác ABCD là hình chữ nhật
C. Điểm \(I(-1; 1)\) là trung điểm của \(AC\)
D. \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \)
Video hướng dẫn giải
Lời giải chi tiết
Trắc nghiệm:
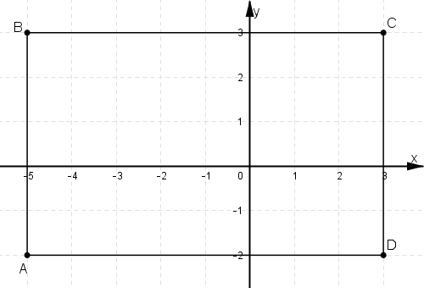
Từ hình vẽ ta thấy ABCD là hình chữ nhật.
Chọn B.
Tự luận:
Ta có:
\(\begin{array}{l}
\overrightarrow {AB} = \left( { - 5 + 5;3 + 2} \right) = \left( {0;5} \right)\\
\overrightarrow {DC} = \left( {3 - 3;3 + 2} \right) = \left( {0;5} \right)\\
\Rightarrow \overrightarrow {AB} = \overrightarrow {DC}
\end{array}\)
Mà \(\overrightarrow {AD} = \left( {3 + 5; - 2 + 2} \right) = \left( {8;0} \right)\) nên \(\overrightarrow {AB} ,\overrightarrow {AD} \) không cùng phương.
Do đó ABCD là hình bình hành.
Mà \(\overrightarrow {AB} = 5\overrightarrow j \) nên cùng phương với \(\overrightarrow j \).
\(\overrightarrow {AD} = 8\overrightarrow i \) nên cùng phương với \(\overrightarrow i \)
Lại có \(\overrightarrow i \) và \(\overrightarrow j \) có phương vuông góc nhau nên AB vuông góc AD.
Vậy ABCD là hình chữ nhật.
Do đó chọn B.
Ngoài ra, A sai vì \(\overrightarrow {AB} ;\overrightarrow {CD} \) ngược hướng.
C sai vì trung điểm AC có tọa độ \(\left( { - 1;\frac{1}{2}} \right)\)
D sai vì:
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} = \left( { - 5 - 5; - 2 + 3} \right) = \left( { - 10;1} \right)\\
\overrightarrow {OC} = \left( {3;3} \right)\\
\Rightarrow \overrightarrow {OA} + \overrightarrow {OB} \ne \overrightarrow {OC}
\end{array}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 14 trang 30 SGK Hình học 10
- Bài 15 trang 30 SGK Hình học 10
- Bài 16 trang 31 SGK Hình học 10
- Bài 17 trang 31 SGK Hình học 10
- Bài 18 trang 31 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
