-
ĐẠI SỐ - SBT TOÁN 10 NÂNG CAO
-
Chương 1: Mệnh đề - Tập hợp
-
Chương 2: Hàm số
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT VÀ BẬC HAI
- Bài 1. Đại cương về phương trình
- Bài 2. Phương trình bậc nhất và bậc hai một ẩn
- Bài 3. Một số phương trình quy về phương trình bậc nhất hoặc bậc hai
- Bài 4. Phương trình và hệ phương trình bậc nhất nhiều ẩn
- Bài 5. Một số ví dụ về hệ phương trình bậc hai hai ẩn
- Bài tập Ôn tập chương III - Phương trình bậc nhất và bậc hai
-
CHƯƠNG IV. BẤT ĐẲNG THỨC VÀ BẤT PHƯƠNG TRÌNH
- Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
- Bài 2. Đại cương về bất phương trình
- Bài 3. Bất phương trình và hệ bất phương trình bậc nhất một ẩn
- Bài 4. Dấu của nhị thức bậc nhất
- Bài 5. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
- Bài 6. Dấu của tam thức bậc hai
- Bài 7. Bất phương trình bậc hai
- Bài 8. Một số phương trình và bất phương trình quy về bậc hai
- Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
-
CHƯƠNG V. THỐNG KÊ
-
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
-
BÀI TẬP ÔN TẬP CUỐI NĂM - ĐẠI SỐ 10 NÂNG CAO
-
-
HÌNH HỌC-SBT TOÁN 10 NÂNG CAO
Giải SBT toán hình học và đại số 10 nâng cao
Bài tập Ôn tập chương II - Tích vô hướng của hai vectơ ..
Bài 83 trang 51 SBT Hình học 10 Nâng cao
Giải bài tập Bài 83 trang 51 SBT Hình học 10 Nâng cao
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Cho tam giác đều \(ABC\) có \(I, J\) lần lượt là trung điểm của \(AB, AC\). Tìm \(\cos (\overrightarrow {AB} ,\overrightarrow {AC} ), \cos (\overrightarrow {AB} ,\overrightarrow {BC} ), \) \( \cos (\overrightarrow {BJ} ,\overrightarrow {BC} ), \cos (\overrightarrow {AB} ,\overrightarrow {BJ} ),\) \( \cos (\overrightarrow {BJ} ,\overrightarrow {CI} ). \)
Lời giải chi tiết
(h.69).
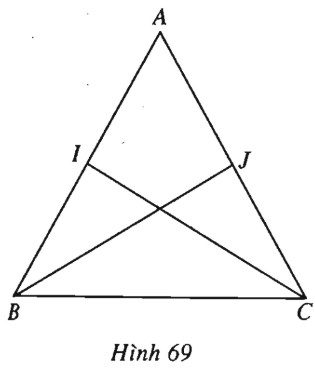
\(\begin{array}{l}\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \cos {60^0} = \dfrac{1}{2}.\\\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \cos {120^0} = - \dfrac{1}{2}.\\\cos \left( {\overrightarrow {BJ} ,\overrightarrow {BC} } \right) = \cos {30^0} = \dfrac{{\sqrt 3 }}{2}.\\\cos \left( {\overrightarrow {AB} ,\overrightarrow {BJ} } \right) = \cos {150^0} = - \dfrac{{\sqrt 3 }}{2}.\\\cos \left( {\overrightarrow {BJ} ,\overrightarrow {CI} } \right) = \cos {120^0} = - \dfrac{1}{2}.\end{array}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 84 trang 51 SBT Hình học 10 Nâng cao
- Bài 85 trang 51 SBT Hình học 10 Nâng cao
- Bài 86 trang 51 SBT Hình học 10 Nâng cao
- Bài 87 trang 51 SBT Hình học 10 Nâng cao
- Bài 88 trang 51 SBT Hình học 10 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
