Bài 7 trang 70 SGK Hình học 10 nâng cao

Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là

Đề bài

Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là

\({b^2} + {c^2} = 5{a^2}\)

Lời giải chi tiết

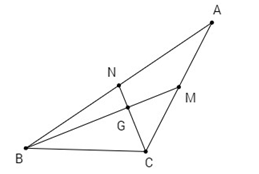
Gọi G là giao điểm của hai trung tuyến BM, CN hay G là trọng tâm tam giác. Ta có:

\(\begin{array}{l}
BG = \frac{2}{3}BM\\
\Rightarrow B{G^2} = \frac{4}{9}B{M^2}\\
= \frac{4}{9}.\left( {\frac{{B{A^2} + B{C^2}}}{2} - \frac{{A{C^2}}}{4}} \right)\\
= \frac{{2\left( {B{A^2} + B{C^2}} \right) - A{C^2}}}{9}
\end{array}\)

\(\begin{array}{l}
CG = \frac{2}{3}CN\\
\Rightarrow C{G^2} = \frac{4}{9}C{N^2}\\
= \frac{4}{9}.\left( {\frac{{C{A^2} + C{B^2}}}{2} - \frac{{B{A^2}}}{4}} \right)\\
= \frac{{2\left( {C{A^2} + C{B^2}} \right) - B{A^2}}}{9}
\end{array}\)

Do đó \(BM \bot CN \Leftrightarrow BG \bot CG\)

\( \Leftrightarrow \Delta BGC\) vuông tại G

\(\Leftrightarrow \,\,B{G^2} + C{G^2} = B{C^2}\)

\(\begin{array}{l}
\Leftrightarrow \frac{{2\left( {B{A^2} + B{C^2}} \right) - A{C^2}}}{9} + \frac{{2\left( {C{A^2} + C{B^2}} \right) - A{B^2}}}{9} = B{C^2}\\
\Leftrightarrow \frac{{2B{A^2} + 2B{C^2} - A{C^2} + 2C{A^2} + 2C{B^2} - A{B^2}}}{9} = B{C^2}\\
\Leftrightarrow \frac{{A{B^2} + 4B{C^2} + A{C^2}}}{9} = B{C^2}\\
\Leftrightarrow A{B^2} + 4B{C^2} + A{C^2} = 9B{C^2}\\
\Leftrightarrow A{B^2} + A{C^2} = 5B{C^2}\\
\Rightarrow {c^2} + {b^2} = 5{a^2}
\end{array}\)

Cách khác:

Loigiaihay.com

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 6 phiếu

Bài tiếp theo

Bài 8 trang 70 SGK Hình học 10 nâng cao
Trong các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất.
Bài 9 trang 70 SGK Hình học 10 nâng cao
Cho tam giác ABC có
Bài 10 trang 71 SGK Hình học 10 nâng cao
Cho tam giác ABC. Chứng minh rằng
Bài 11 trang 71 SGK Hình học 10 nâng cao
Cho hai đường tròn
Bài 12 trang 71 SGK Hình học 10 nâng cao
Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.
Giải bài 6 trang 70 SGK Hình học 10 nâng cao
Trong mặt phẳng tọa độ, cho
Bài 5 trang 70 SGK Hình học 10 nâng cao
Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho
Bài 4 trang 70 SGK Hình học 10 nâng cao
Trên hình 63 có vẽ hai tam giác vuông cân ABC và A'B'C' có chung đỉnh A.
Bài 3 trang 70 SGK Hình học 10 nâng cao
Cho hình bình hành ABCD. Tìm tập hợp các điểm M sao cho
Bài 2 trang 69 SGK Hình học 10 nâng cao
Gọi G là trọng tâm tam giác ABC.
Bài 1 trang 69 SGK Hình học 10 nâng cao
Chứng minh các công thức sau