 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Ôn tập chương II - Tích vô hướng của hai vectơ và ứng d..
Ôn tập chương II - Tích vô hướng của hai vectơ và ứng d..
Bài 4 trang 70 SGK Hình học 10 nâng cao
Trên hình 63 có vẽ hai tam giác vuông cân ABC và A'B'C' có chung đỉnh A.
Trên hình 63 có vẽ hai tam giác vuông cân ABC và AB'C' có chung đỉnh A. Gọi I và J lần lượt là trung điểm của hai đoạn thẳng BB' và CC'.
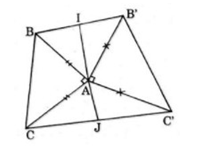
Chứng minh rằng
LG a
\(AI \bot C{C'}\,,\,AJ \bot B{B'}\,\)
Phương pháp giải:
Để chứng minh các đường thẳng vuông góc, ta thực hiện nhân vô hướng các véc tơ và kiểm tra tích đó bằng 0.
Lời giải chi tiết:
Vì I là trung điểm BB' và J là trung điểm CC' nên:
\(\overrightarrow {AI} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {A{B'}} )\)
\(\overrightarrow {AJ} = {1 \over 2}(\overrightarrow {AC} + \overrightarrow {A{C'}} )\)
\(\eqalign{
& \Rightarrow \,\,\overrightarrow {AI} .\,\overrightarrow {C{C'}} \cr&= {1 \over 2}(\overrightarrow {AB} + \overrightarrow {A{B'}} ).\,(\overrightarrow {A{C'}} - \overrightarrow {AC} ) \cr
& = {1 \over 2}(\overrightarrow {AB} .\,\overrightarrow {A{C'}} - \overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {A{B'}} .\,\overrightarrow {A{C'}} - \overrightarrow {A{B'}} .\,\overrightarrow {AC} ) \cr} \)
Vì \(AB \bot AC\,,\,\,A{B'} \bot A{C'}\,\) nên \(\overrightarrow {AB} .\,\overrightarrow {AC} = \overrightarrow {A{B'}} .\,\overrightarrow {A{C'}} = 0\)
\(\Rightarrow \overrightarrow {AI} .\overrightarrow {CC'} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AC'} - \overrightarrow {AB'} .\overrightarrow {AC} } \right)\)
Mặt khác
\(\eqalign{
& \overrightarrow {AB} .\,\overrightarrow {A{C'}} = AB.\,A{C'}.\cos \widehat {BA{C'}} \cr
& \overrightarrow {A{B'}} .\,\overrightarrow {AC} = A{B'}.\,AC.\cos \widehat {{B'}AC} \cr} \)
Do ABC, AB’C’ vuông cân tại A nên AC’=AC,AB’=AB
Lại có:
\(\begin{array}{l}\widehat {BAC'} = \widehat {BAB'} + \widehat {B'AC'} = \widehat {BAB'} + {90^0}\\\widehat {B'AC} = \widehat {B'AB} + \widehat {BAC} = \widehat {B'AB} + {90^0}\\ \Rightarrow \widehat {BAC'} = \widehat {B'AC}\\ \Rightarrow \cos \widehat {BAC'} = \cos \widehat {B'AC}\end{array}\)
Do đó,
\(\overrightarrow {AB} .\overrightarrow {AC'} = \overrightarrow {AB'} .\overrightarrow {AC} \)
\(\Rightarrow \overrightarrow {AB} .\overrightarrow {AC'} - \overrightarrow {AB'} .\overrightarrow {AC} = 0\)
\( \Rightarrow \overrightarrow {AI} .\overrightarrow {CC'} = 0 \Leftrightarrow AI \bot CC'\)
Tương tự \(\overrightarrow {AJ} .\,\overrightarrow {B{B'}} \)
\(= {1 \over 2}(\overrightarrow {AC} + \overrightarrow {A{C'}} ).\,(\overrightarrow {A{B'}} - \overrightarrow {AB} )\)
\(\eqalign{
& = {1 \over 2}(\overrightarrow {AC} .\,\overrightarrow {A{B'}} - \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {A{C'}} .\,\overrightarrow {A{B'}} - \overrightarrow {A{C'}} .\,\overrightarrow {AB} )\cr
& = \frac{1}{2}\left( {\overrightarrow {AC} .\overrightarrow {AB'} - \overrightarrow {AC'} .\overrightarrow {AB} } \right) = 0\cr&\Rightarrow \,\,AJ \bot B{B'} \cr} \)
LG b
\(B{C'}\,\, \bot {B'}C\,\,\)
Lời giải chi tiết:
Ta có
\(\eqalign{
& \overrightarrow {B{C'}} .\,\overrightarrow {{B'}C} \cr&= (\overrightarrow {A{C'}} - \overrightarrow {AB} ).\,(\overrightarrow {AC} - \overrightarrow {A{B'}} ) \cr
& = \overrightarrow {A{C'}} .\,\overrightarrow {AC} - \overrightarrow {A{C'}} .\,\overrightarrow {A{B'}} - \overrightarrow {AB} .\,\overrightarrow {AC} + \overrightarrow {AB} .\,\overrightarrow {A{B'}} \cr} \)
\( = \overrightarrow {AC'} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AB'} \)
(vì \(\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB'} .\overrightarrow {AC'} = 0\))
\(\overrightarrow {AB} .\,\overrightarrow {A{B'}} = AB.A{B'}.\cos \widehat {BA{B'}}\)
\(\overrightarrow {AC} .\,\overrightarrow {A{C'}}\)\( = AC.A{C'}.\cos ({180^0} - \widehat {BA{B'}}) \)
\(= - \overrightarrow {AB} .\,\overrightarrow {A{B'}}.\)
Do đó: \(\overrightarrow {AC'} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AB'} \)\(= - \overrightarrow {AB} .\overrightarrow {AB'} + \overrightarrow {AB} .\overrightarrow {AB'} = 0\)
Suy ra \(\overrightarrow {B{C'}} .\,\overrightarrow {{B'}C} =\overrightarrow 0\)
Vậy \(B{C'} \bot {B'}C\).
Loigiaihay.com












Danh sách bình luận