 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 Bài 2. Tích vô hướng của hai vectơ
Bài 2. Tích vô hướng của hai vectơ
Bài 7 trang 52 SGK Hình học 10 nâng cao
Cho bốn điểm bất kì A, B, C, D. Chứng minh rằng
Đề bài
Cho bốn điểm bất kì \(A, B, C, D\). Chứng minh rằng:
\(\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0\).
Từ đó suy ra một cách chứng minh định lí: “Ba đường cao của một tam giác đồng quy”.
Lời giải chi tiết
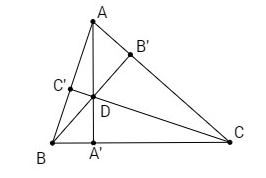
Ta có
\(\eqalign{
& \,\,\,\,\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} \cr
& = \overrightarrow {DA} (\overrightarrow {DC} - \overrightarrow {DB} ) + \overrightarrow {DB} (\overrightarrow {DA} - \overrightarrow {DC} ) + \overrightarrow {DC} (\overrightarrow {DB} - \overrightarrow {DA} ) \cr
& = \overrightarrow {DA} \overrightarrow {DC} - \overrightarrow {DA} \overrightarrow {DB} + \overrightarrow {DB} \overrightarrow {DA} - \overrightarrow {DB} \overrightarrow {DC} + \overrightarrow {DC} \overrightarrow {DB} - \overrightarrow {DC} \overrightarrow {DA} = 0 \cr} \)
Gọi \(D\) là giao điểm của hai đường cao \(AA', BB'\) của tam giác \(ABC\).
Ta có \(\overrightarrow {DA} .\overrightarrow {BC} = 0\,;\,\,\overrightarrow {DB} .\overrightarrow {CA} = 0\)
Mà \(\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0\)
Từ đó suy ra \(\overrightarrow {DC} .\overrightarrow {AB} = 0\), do đó \(DC \bot AB\).
Vậy \(D\) nằm trên đường cao \(CC'\) của tam giác \(ABC\), tức là ba đường cao trong tam giác đồng quy.
Cách khác:
Ta có thể chứng minh đẳng thức tích vô hướng bằng cách khác như sau:
Loigiaihay.com













Danh sách bình luận