Bài 5 trang 51 SGK Hình học 10 nâng cao

Cho tam giác ABC.

Đề bài

Cho tam giác \(ABC\). Tổng \((\overrightarrow {AB} ,\,\overrightarrow {BC} ) + (\overrightarrow {BC} ,\,\overrightarrow {CA} ) + (\overrightarrow {CA} ,\,\overrightarrow {AB} )\) có thể nhận giá trị nào trong các giá trị sau : \({90^0}\,;\,{180^0}\,;\,{270^{0\,}}\,;\,{360^0}\) ?

Lời giải chi tiết

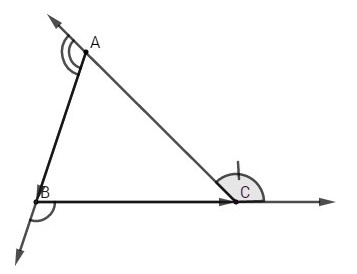
Ta có

\((\overrightarrow {AB} ,\,\overrightarrow {BC} ) = {180^0} - \widehat B\) vì góc \((\overrightarrow {AB} ,\,\overrightarrow {BC} )\) và \(\widehat B\) là hai góc kề bù.

\((\overrightarrow {BC} ,\,\overrightarrow {CA} ) = {180^0} - \widehat C\) vì góc \((\overrightarrow {BC} ,\,\overrightarrow {CA} )\) và \(\widehat C\) là hai góc kề bù.

\((\overrightarrow {CA} ,\,\overrightarrow {AB} ) = {180^0} - \widehat A\) vì góc \((\overrightarrow {CA} ,\,\overrightarrow {AB} )\) và \(\widehat A\) là hai góc kề bù.

Do đó \((\overrightarrow {AB} ,\,\overrightarrow {BC} ) + (\overrightarrow {BC} ,\,\overrightarrow {CA} ) + (\overrightarrow {CA} ,\,\overrightarrow {AB} ) \)

\(\begin{array}{l}
= {180^0} - \widehat B + {180^0} - \widehat C + {180^0} - \widehat A\\
= {540^0} - \left( {\widehat B + \widehat C + \widehat A} \right)\\
= {540^0} - {180^0}\\
= {360^0}
\end{array}\)

Loigiaihay.com