 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Bài 1. Lũy thừa với số mũ hữu tỉ
Bài 1. Lũy thừa với số mũ hữu tỉ
Bài 5 trang 76 SGK Đại số và Giải tích 12 Nâng cao
Đơn giản biểu thức ( với a, b là những số dương)
Đơn giản biểu thức ( với a, b là những số dương)
LG a
\({{{{\left( {\root 4 \of {{a^3}{b^2}} } \right)}^4}} \over {\root 3 \of {\sqrt {{a^{12}}{b^6}} } }}\)
Lời giải chi tiết:
\({{{{\left( {\root 4 \of {{a^3}{b^2}} } \right)}^4}} \over {\root 3 \of {\sqrt {{a^{12}}{b^6}} } }} = {{{a^3}{b^2}} \over {\root 6 \of {{a^{12}}{b^6}} }} = {{{a^3}{b^2}} \over {{a^2}b}} = ab\)
LG b
\({{{a^{{1 \over 3}}} - {a^{{7 \over 3}}}} \over {{a^{{1 \over 3}}} - {a^{{4 \over 3}}}}} - {{{a^{ - {1 \over 3}}} - {a^{{5 \over 3}}}} \over {{a^{{2 \over 3}}} + {a^{ - {1 \over 3}}}}}\)
Lời giải chi tiết:
\({{{a^{{1 \over 3}}} - {a^{{7 \over 3}}}} \over {{a^{{1 \over 3}}} - {a^{{4 \over 3}}}}} - {{{a^{ - {1 \over 3}}} - {a^{{5 \over 3}}}} \over {{a^{{2 \over 3}}} + {a^{ - {1 \over 3}}}}} \)
\(= {{{a^{{1 \over 3}}}\left( {1 - {a^2}} \right)} \over {{a^{{1 \over 3}}}\left( {1-a} \right)}} - {{{a^{ - {1 \over 3}}}\left( {1 - {a^2}} \right)} \over {{a^{ - {1 \over 3}}}\left( {a + 1} \right)}} \)
\( = \left( {1 + a} \right) - \left( {1 - a} \right) = 2a.\)
Cách khác:
Loigiaihay.com




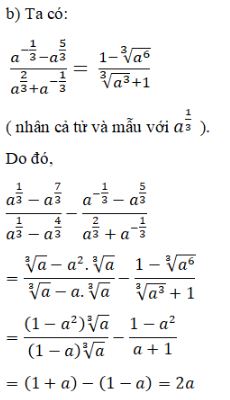








Danh sách bình luận