Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học

Ôn tập chương II - Tích vô hướng của hai vectơ và ứng d..

Bài 5 trang 70 SGK Hình học 10 nâng cao

Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho

Lựa chọn câu để xem lời giải nhanh hơn

Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho \(AM = {1 \over 4}AC.\)

LG a

Tính các cạnh của tam giác BMN

Lời giải chi tiết:

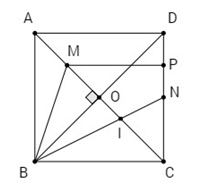
Gọi O là tâm của hình bình hành ABCD thì M là trung điểm AO.

Tam giác ABC vuông tại B nên:

\(\begin{array}{l}
A{C^2} = A{B^2} + B{C^2}\\
\Rightarrow AC = \sqrt {A{B^2} + B{C^2}} \\
= \sqrt {{a^2} + {a^2}} = a\sqrt 2
\end{array}\)

Do đó \(OA = OB = OC = OD \)\(= \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)

\( \Rightarrow OM = \frac{1}{2}OA = \frac{1}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{4}\)

N là trung điểm CD nên \(NC = \frac{1}{2}DC = \frac{a}{2}\).

Ta có:

\(\eqalign{
& B{N^2} = B{C^2} + N{C^2} \cr
& = {a^2} + {{{a^2}} \over 4} = {{5{a^2}} \over 4}\cr&\Rightarrow \,\,BN = {{a\sqrt 5 } \over 2} \cr
& B{M^2} = B{O^2} + O{M^2} \cr
& = {\left( {{{a\sqrt 2 } \over 2}} \right)^2} + {\left( {{{a\sqrt 2 } \over 4}} \right)^2} = {{5{a^2}} \over 8} \cr
& \Rightarrow \,\,BM = {{a\sqrt {10} } \over 4} \cr} \)

Kẻ MP // AD ta có

\(\frac{{MP}}{{AD}} = \frac{{CM}}{{CA}} = \frac{3}{4} \)\(\Rightarrow MP = \frac{3}{4}AD = \frac{{3a}}{4}\)

\(\frac{{CP}}{{CD}} = \frac{{CM}}{{CA}} = \frac{3}{4} \)\(\Rightarrow CP = \frac{3}{4}CD = \frac{{3a}}{4} \)\(\Rightarrow PD = CD - CP = a - \frac{{3a}}{4} = \frac{a}{4}\)

\( \Rightarrow NP = DN - PD = \frac{a}{2} - \frac{a}{4} = \frac{a}{4}\)

Tam giác MNP vuông tại P nên:

\(M{N^2} = M{P^2} + P{N^2} \)\(= {\left( {{{3a} \over 4}} \right)^2} + {\left( {{a \over 4}} \right)^2} = {{10{a^2}} \over {16}}\,\,\)

\(\Rightarrow \,\,MN = {{a\sqrt {10} } \over 4}\)

LG b

Có nhận xét gì về tam giác BMN ? Tính diện tích tam giác đó.

Lời giải chi tiết:

Ta có \(MB = MN\) nên tam giác BMN cân tại M.

Lại có:

\(B{M^2} + M{N^2}\)

\(= {\left( {\frac{{a\sqrt {10} }}{4}} \right)^2} + {\left( {\frac{{a\sqrt {10} }}{4}} \right)^2} \)

\(= \frac{{5{a^2}}}{4} \)

\(= B{N^2}\)

nên tam giác BMN vuông tại M.

Vậy tam giác BMN vuông cân tại M.

Diện tích tam giác BMN là

\({S_{BMN}} = {1 \over 2}MB.MN\)\( = \frac{1}{2}\frac{{a\sqrt {10} }}{4}.\frac{{a\sqrt {10} }}{4}= {{5{a^2}} \over {16}}\)

LG c

Gọi I là giao điểm của BN và AC. Tính CI.

Lời giải chi tiết:

Tam giác DCB có hai đường trung tuyến CO và BN cắt nhau tại I nên I là trọng tâm tam giác BCD

Do đó, \(IC = {2 \over 3}IO = {2 \over 3}.a.{{\sqrt 2 } \over 2} = {{a\sqrt 2 } \over 3}\).

LG d

Tính bán kính đường tròn ngoại tiếp tam giác BDN.

Lời giải chi tiết:

Gọi R là bán kính đường tròn ngoại tiếp tam giác BDN.

Áp dụng định lí sin ta có:

\({{BN} \over {\sin \widehat {BDN}}} = 2R\)

\(\Rightarrow \,\,R = \,{{BN} \over {2\sin {{45}^0}}} = \frac{{\frac{{a\sqrt 5 }}{2}}}{{2.\frac{{\sqrt 2 }}{2}}}= {{a\sqrt {10} } \over 4}\)

Loigiaihay.com

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 7 phiếu

Bài tiếp theo

Giải bài 6 trang 70 SGK Hình học 10 nâng cao
Trong mặt phẳng tọa độ, cho
Bài 7 trang 70 SGK Hình học 10 nâng cao
Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là
Bài 8 trang 70 SGK Hình học 10 nâng cao
Trong các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất.
Bài 9 trang 70 SGK Hình học 10 nâng cao
Cho tam giác ABC có
Bài 10 trang 71 SGK Hình học 10 nâng cao
Cho tam giác ABC. Chứng minh rằng
Bài 11 trang 71 SGK Hình học 10 nâng cao
Cho hai đường tròn
Bài 12 trang 71 SGK Hình học 10 nâng cao
Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.
Bài 4 trang 70 SGK Hình học 10 nâng cao
Trên hình 63 có vẽ hai tam giác vuông cân ABC và A'B'C' có chung đỉnh A.
Bài 3 trang 70 SGK Hình học 10 nâng cao
Cho hình bình hành ABCD. Tìm tập hợp các điểm M sao cho
Bài 2 trang 69 SGK Hình học 10 nâng cao
Gọi G là trọng tâm tam giác ABC.
Bài 1 trang 69 SGK Hình học 10 nâng cao
Chứng minh các công thức sau