Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Bài 3. Giá trị lượng giác của các góc (cung) có liên qu..

Bài 36 trang 207 SGK Đại số 10 Nâng cao


Tính diện tích tam giác A’MA bằng hai cách khác nhau để suy ra: sin2α = 2sinα cosα

Lựa chọn câu để xem lời giải nhanh hơn

Với số \(α,0 < \alpha  < {\pi  \over 2}\), xét điểm M của đường tròn lượng giác xác định bởi 2α , rồi xét tam giác vuông A’MA (A’ đối xứng với A qua tâm O của đường tròn).

LG a

Tính AM2 bằng hai cách khác nhau để suy ra: cos2α = 1 – 2sin2α

Lời giải chi tiết:

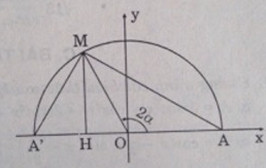
Ta có:

\(\eqalign{
& A{M^2} = \overline {AH} .\overline {{\rm{AA}}} {\rm{' = (}}\overline {AO} + \overline {OH} ).\overline {{\rm{AA}}'} \cr 
& = ( - 1 + \cos 2\alpha )( - 2) = 2(1 - \cos 2\alpha ) \cr} \)

Lại có:

\(\begin{array}{l}
\left\{ \begin{array}{l}
2\alpha = \widehat {AOM} = \widehat {OA'M} + \widehat {OMA'}\\
\widehat {OA'M} = \widehat {OMA'}\left( {\Delta OMA'\,can} \right)
\end{array} \right.\\
\Rightarrow 2\alpha = \widehat {OA'M} + \widehat {OMA'} = 2\widehat {OA'M}\\
\Rightarrow \widehat {OA'M} = \alpha \\
\Rightarrow AM = AA'\sin \widehat {AA'M} = 2\sin \alpha \\
\Rightarrow A{M^2} = 4{\sin ^2}\alpha
\end{array}\)

Vậy:

\(\begin{array}{l}
\Rightarrow 2\left( {1 - \cos 2\alpha } \right) = 4{\sin ^2}\alpha \\
\Leftrightarrow 1 - \cos 2\alpha = 2{\sin ^2}\alpha \\
\Leftrightarrow \cos 2\alpha = 1 - 2{\sin ^2}\alpha
\end{array}\)

Cách khác:

LG b

Tính diện tích tam giác A’MA bằng hai cách khác nhau để suy ra:

sin2α = 2sinα cosα

Lời giải chi tiết:

Ta có: \({S_{A'MA}} = {1 \over 2}AA'.MH = MH = \sin 2\alpha \)

Lại có:

\({S_{A'MA}} = {1 \over 2}A'M.AM \) \(= {1 \over 2}A'A\cos \alpha .A'A\sin \alpha  \)

\(= 2\sin \alpha \cos \alpha \)

Vậy: \(\sin2α  = 2\sinα \cosα\)

LG c

Chứng minh: \(\sin {\pi  \over 8} = {1 \over 2}\sqrt {2 - \sqrt 2 } ;\) \(\cos {\pi  \over 8} = {1 \over 2}\sqrt {2 + \sqrt 2 } \) rồi tính các giá trị lượng giác của các góc \({{3\pi } \over 8}\) và \({{5\pi } \over 8}\)

Phương pháp giải:

Sử dụng công thức nhân đôi vừa chứng minh ở câu a, b.

Xuất phát từ \(\cos \frac{\pi }{4},\sin \frac{\pi }{4}\) để tính \(\cos \frac{\pi }{8},\sin \frac{\pi }{8}\).

Lời giải chi tiết:

Ta có: \(\cos {\pi  \over 4} = 1 - 2{\sin ^2}{\pi  \over 8}\) nên:

\(\eqalign{
& {\sin ^2}{\pi \over 8} = {1 \over 2}(1 - {{\sqrt 2 } \over 2}) = {{2 - \sqrt 2 } \over 4} \cr 
& \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \cr 
&\cos \frac{\pi }{8} = \sqrt {1 - {{\sin }^2}\frac{\pi }{8}}  \cr &= \sqrt {1 - \frac{{2 - \sqrt 2 }}{4}}  = \frac{{\sqrt {2 + \sqrt 2 } }}{2} \cr 
& {{3\pi } \over 8} = {\pi \over 2} - {\pi \over 8} \cr &\Rightarrow \left\{ \matrix{
\cos {{3\pi } \over 8} = \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \hfill \cr 
\sin {{3\pi } \over 8} = \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \hfill \cr 
\tan {{3\pi } \over 8} = \cot {\pi \over 8} = \sqrt 2 + 1 \hfill \cr 
\cot {{3\pi } \over 8} = \tan {\pi \over 8} = \sqrt 2 - 1 \hfill \cr} \right. \cr 
& {{5\pi } \over 8} = {\pi \over 2} + {\pi \over 8} \cr &\Rightarrow \left\{ \matrix{
\cos {{5\pi } \over 8} = - \sin {\pi \over 8} = {{\sqrt {2 - \sqrt 2 } } \over 2} \hfill \cr 
\sin {{5\pi } \over 8} = \cos {\pi \over 8} = {{\sqrt {2 + \sqrt 2 } } \over 2} \hfill \cr 
\tan {{5\pi } \over 8} = - \cot {\pi \over 8} = - \sqrt 2 - 1 \hfill \cr 
\cot {{5\pi } \over 8} = - \tan {\pi \over 8} = 1 - \sqrt 2 \hfill \cr} \right. \cr} \)

Loigiaihay.com


Bình chọn:
4.2 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store