 Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
 Bài 6. Ứng dụng tích phân để tính thể tích vật thể
Bài 6. Ứng dụng tích phân để tính thể tích vật thể
Bài 34 Trang 174 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích hình phẳng giới hạn bởi:
Tính diện tích hình phẳng giới hạn bởi:
LG a
Đồ thị các hàm số \(y = x, y = 1\) và \(y = {{{x^2}} \over 4}\) trong miền \(x \ge 0,y \le 1.\)
Phương pháp giải:
Dựng hình, tính diện tích miền cần tính và kết luận.
Lời giải chi tiết:
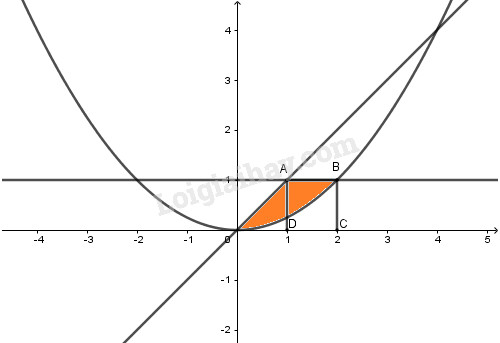
Diện tích hình thang \(OABC\) là:
\({S_1} = (2 + 1){1 \over 2} = {3 \over 2}\)
Diện tích tam giác cong \(OBC\) là hình phẳng giới hạn bởi: \(y = 0,x = 2,y = {{{x^2}} \over 4}\) là:
\({S_2} = \int\limits_0^2 {{{{x^2}} \over 4}} dx = \left. {{{{x^3}} \over {12}}} \right|_0^2 = {2 \over 3}\)
Diện tích cần tìm là \(S = {S_1} - {S_2} = {3 \over 2} - {2 \over 3} = {5 \over 6}\).
Cách 2:
Diện tích hình phẳng cần tìm chính là tổng diện tích tam giác cong OAD và tam giác cong ADB.
Diện tích tam giác cong OAD là:
\({S_{OAD}} = \int\limits_0^1 {\left( {x - \dfrac{{{x^2}}}{4}} \right)dx} \) \( = \left. {\left( {\dfrac{{{x^2}}}{2} - \dfrac{{{x^3}}}{{12}}} \right)} \right|_0^1 = \dfrac{5}{{12}} - 0 = \dfrac{5}{{12}}\)
Diện tích tam giác cong ADB là:
\({S_{ADB}} = \int\limits_1^2 {\left( {1 - \dfrac{{{x^2}}}{4}} \right)dx} \) \( = \left. {\left( {x - \dfrac{{{x^3}}}{{12}}} \right)} \right|_1^2 = \dfrac{4}{3} - \dfrac{{11}}{{12}} = \dfrac{5}{{12}}\)
Vật diện tích hình phẳng cần tìm là:
\(\dfrac{5}{{12}} + \dfrac{5}{{12}} = \dfrac{5}{6}\)
Cách 3.
Ta có: \(y = \dfrac{{{x^2}}}{4} \Leftrightarrow {x^2} = 4y\) \( \Leftrightarrow x = 2\sqrt y \) (do ta chỉ xét miền \(x \ge 0\))
Gọi hình phẳng đã cho là hình phẳng giới hạn bởi đường cong có phương trình x=2 √y, đường thẳng x = y và y = 0 và đường thẳng y = 1. Diện tích cần tìm là:
\(S = \int\limits_0^1 {\left( {2\sqrt y - y} \right)dy}\) \( = \left. {\left( {2.\dfrac{{{y^{\dfrac{3}{2}}}}}{{\dfrac{3}{2}}} - \dfrac{{{y^2}}}{2}} \right)} \right|_0^1\) \( = \left. {\left( {\dfrac{4}{3}y\sqrt y - \dfrac{{{y^2}}}{2}} \right)} \right|_0^1 = \dfrac{5}{6} - 0 = \dfrac{5}{6}\)
LG b
Đồ thị hai hàm số \(y = {x^4} - 4{x^2} + 4,y = {x^2}\), trục tung và đường thẳng \(x = 1\)
Phương pháp giải:
Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right),\) \(x = a,x = b\).
+) B1: Tìm nghiệm \(a \le {x_1} < {x_2} < ... < {x_n} \le b\) của phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\).
+) B2: Tính diện tích theo công thức:
\(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
\( = \int\limits_a^{{x_1}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + \int\limits_{{x_1}}^{{x_2}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + ... + \int\limits_{{x_{n - 1}}}^{{x_n}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + \int\limits_{{x_n}}^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
\( = \left| {\int\limits_a^{{x_1}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\)\( + \left| {\int\limits_{{x_1}}^{{x_2}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\) \( + ... + \left| {\int\limits_{{x_{n - 1}}}^{{x_n}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\) \( + \left| {\int\limits_{{x_n}}^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\)
Lời giải chi tiết:
Cách 1:
Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^4} - 4{x^2} + 4 = {x^2} \Leftrightarrow \left[ \matrix{
{x^2} = 1 \hfill \cr
{x^2} = 4 \hfill \cr} \right. \) \(\Leftrightarrow \left[ \matrix{
x = \pm 1 \hfill \cr
x = \pm 2 \hfill \cr} \right.\)
Ta có: \(-2<-1<0<1<2\) nên
\(S=\int\limits_{0}^{1}{\left| {{x}^{4}}-4{{x}^{2}}+4-{{x}^{2}} \right|dx}\) \(=\int\limits_{0}^{1}{\left| {{x}^{4}}-5{{x}^{2}}+4 \right|dx}\) \(=\left| \int\limits_{0}^{1}{\left( {{x}^{4}}-5{{x}^{2}}+4 \right)dx} \right|\) \(=\left| \left. \left( \dfrac{{{x}^{5}}}{5}-\dfrac{5{{x}^{3}}}{3}+4x \right) \right|_{0}^{1} \right|\) \(=\left| \dfrac{38}{15} \right|=\dfrac{38}{15}\)
Cách 2:
Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^4} - 4{x^2} + 4 = {x^2} \Leftrightarrow \left[ \matrix{
{x^2} = 1 \hfill \cr
{x^2} = 4 \hfill \cr} \right. \) \(\Leftrightarrow \left[ \matrix{
x = \pm 1 \hfill \cr
x = \pm 2 \hfill \cr} \right.\)
Ta có:
\(\eqalign{
& S = \int\limits_0^1 {\left| {{x^4} - 4{x^2} + 4 - {x^2}} \right|} dx \cr &= \int\limits_0^1 {\left| {{x^4} - 5{x^2} + 4} \right|} dx \cr
& = \int\limits_0^1 {({x^4} - 5{x^2}} + 4)dx \cr &= \left. {\left( {{{{x^5}} \over 5} - {{5{x^3}} \over 3} + 4x} \right)} \right|_0^1 = {{38} \over {15}} \cr} \)
LG c
Đồ thị các hàm số \(y = {x^2},y = 4x - 4\) và \(y = -4x – 4\).
Phương pháp giải:
Dựng hình suy ra các công thức tính diện tích.
Lời giải chi tiết:
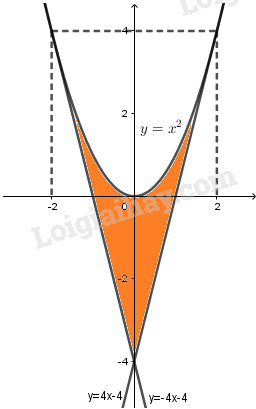
Phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^2}\) và đường thẳng \(y = 4x – 4\) là:
\(\eqalign{
& {x^2} = 4x - 4 \Leftrightarrow {x^2} - 4x + 4 = 0 \cr
& \Leftrightarrow {(x - 2)^2} = 0 \Leftrightarrow x = 2. \cr} \)
Phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^2}\) và đường thẳng
\(y = -4x – 4\) là:
\(\eqalign{
& {x^2} = - 4x - 4 \Leftrightarrow {x^2} + 4x + 4 = 0 \cr
& \Leftrightarrow {(x + 2)^2} = 0 \Leftrightarrow x = - 2. \cr} \)
\(\eqalign{
& S = \int\limits_{ - 2}^0 {\left| {{x^2} - \left( { - 4x - 4} \right)} \right|dx} \cr &+ \int\limits_0^2 {\left| {{x^2} - \left( {4x - 4} \right)} \right|dx}\cr & = \int\limits_{ - 2}^0 {({x^2} + 4x + 4)} dx \cr &+ \int\limits_0^2 {({x^2} - 4x + 4)} dx \cr
& = \left. {\left( {{{{x^3}} \over 3} + 2{x^2} + 4x} \right)} \right|_{ - 2}^0 \cr &+ \left. {\left( {{{{x^3}} \over 3} - 2{x^2} + 4x} \right)} \right|_0^2 \cr &= {8 \over 3} + {8 \over 3} = {{16} \over 3} \cr} \)
Cách khác:
Do tính đối xứng qua Oy của parabol y=x2 nên diện tích hình phẳng cần tìm bằng 2 lần diện tích tam giác cong giới hạn bởi đồ thị hàm số \(y = {x^2}\), trục tung, đường thẳng \(y = 4x - 4\). Khi đó,
\(S = 2\int\limits_0^2 {\left( {{x^2} - 4x + 4} \right)dx} \) \( = 2\left. {\left( {\dfrac{{{x^3}}}{3} - 2{x^2} + 4x} \right)} \right|_0^2\) \( = 2\left( {\dfrac{8}{3} - 0} \right) = \dfrac{{16}}{3}\)
Loigiaihay.com












Danh sách bình luận