Bài 12 trang 71 SGK Hình học 10 nâng cao

Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.

LG a

Chứng minh rằng \(A{B^2} + C{D^2}\) không đổi.

Lời giải chi tiết:

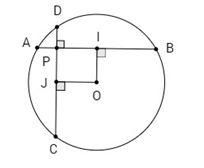
Gọi I và J theo thứ tự là trung điểm của AB và CD.

Theo định lí quan hệ giữa đường kính và dây ta có:

OI ⊥ AB; OJ ⊥ CD;

Do đó tứ giác OIPJ là hình chữ nhật.

Ta có:

AB² + CD² = (2AI)² + (2DJ)²

= 4 AI² + 4DJ² = 4. (AO² – OI² ) + 4(DO² – OJ² )

=4. (R² – OI² ) + 4(R² – OJ² )

= 4( 2R² – OI² – OJ² )

= 4.[2R² – (OI² + OJ²) ]

= 4. ( 2R² – OP²) ( vì OI² + OJ² = OI² + IP² = OP² )

= 8R² – 4. OP²

(không đổi vì R không đổi, O và P cố định nên OP không đổi)

LG b

Chứng minh rằng \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P.

Lời giải chi tiết:

Phương tích của điểm P với đường tròn:

\(\begin{array}{l}{P_{P/\left( O \right)}} = \overrightarrow {PA} .\overrightarrow {PB} = O{P^2} - {R^2}\\{P_{P/\left( O \right)}} = \overrightarrow {PC} .\overrightarrow {PD} = O{P^2} - {R^2}\end{array}\)

Ta có

\(\eqalign{
& P{A^2} + P{B^2} + P{C^2} + P{D^2} \cr&= {(\overrightarrow {PA} - \overrightarrow {PB} )^2} + {(\overrightarrow {PC} - \overrightarrow {PD} )^2} \cr&+ 2.\overrightarrow {PA} .\,\overrightarrow {PB} + 2\overrightarrow {PC} .\,\overrightarrow {PD} \cr
& = {\overrightarrow {BA} ^2} + {\overrightarrow {DC} ^2} + 2\left( {\overrightarrow {PA} .\overrightarrow {PB} + \overrightarrow {PC} .\overrightarrow {PD} } \right) \cr&= A{B^2} + C{D^2} + 2\left( {O{P^2} - {R^2} + O{P^2} - {R^2}} \right)\cr&= A{B^2} + C{D^2} + 2(2P{O^2} - 2{R^2}) \cr
& = 8{R^2} - 4O{P^2} + 4P{O^2} - 4{R^2} \cr
& = 4{R^2} \cr} \)

Vậy \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P.

Loigiaihay.com

👉

Giải bài nhanh với AI Hay: