Bài 12 trang 52 SGK Hình học 10 nâng cao

Cho đoạn thẳng AB cố định, AB = 2a

Đề bài

Cho đoạn thẳng \(AB\) cố định, \(AB = 2a\) và một số \({k^2}\). Tìm tập hợp các điểm \(M\) sao cho \(M{A^2} - M{B^2} = {k^2}\)

Lời giải chi tiết

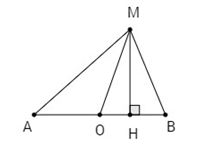
Gọi \(O\) là trung điểm đoạn \(AB, H\) là hình chiếu của \(M\) lên \(AB\). Ta có

\(\eqalign{
& M{A^2} - M{B^2} = {k^2}\cr& \Leftrightarrow \,\,{\overrightarrow {MA} ^2} - {\overrightarrow {MB} ^2} = {k^2} \cr
& \Leftrightarrow (\overrightarrow {MA} + \overrightarrow {MB} ).\,(\overrightarrow {MA} - \overrightarrow {MB} ) = {k^2} \cr
& \Leftrightarrow 2\overrightarrow {MO} .\,\overrightarrow {BA} = {k^2}\, \cr
& \Leftrightarrow 2\left( {\overrightarrow {MH} + \overrightarrow {HO} } \right).\overrightarrow {BA}=k^2 \cr
& \Leftrightarrow 2\overrightarrow {MH} .\overrightarrow {BA} + 2\overrightarrow {HO} .\overrightarrow {BA} = {k^2}\cr&\Leftrightarrow 2\overrightarrow {HO} .\,\overrightarrow {BA} = {k^2} \cr} \)

(Vì \(\overrightarrow {MH} .\overrightarrow {BA} = \overrightarrow 0 \))

\(\begin{array}{l}
\Leftrightarrow 2HO.BA\cos \left( {\overrightarrow {HO} ,\overrightarrow {BA} } \right) = {k^2}\\
\Leftrightarrow 2HO.BA.\cos {0^0} = {k^2}\\
\Leftrightarrow 2HO.BA = {k^2}\\
\Leftrightarrow HO = \frac{{{k^2}}}{{2BA}} = \frac{{{k^2}}}{{2.2a}} = \frac{{{k^2}}}{{4a}}
\end{array}\)

Suy ra \(H\) cố định nằm trên tia \(OB\) và \(OH = {{{k^2}} \over {4a}}\).

Do \(H\) là hình chiếu của \(M\) lên \(AB\) nên tập hợp các điểm \(M\) là đường thẳng vuông góc với \(AB\) tại \(H, H\) nằm trên tia \(OB\) sao cho \(OH = {{{k^2}} \over {4a}}\).

Loigiaihay.com

👉

Giải bài nhanh với AI Hay: