Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học Ôn tập chương II - Tích vô hướng của hai vectơ và ứng d..

Bài 11 trang 71 SGK Hình học 10 nâng cao


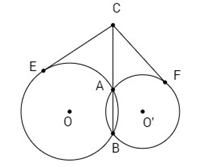
Cho hai đường tròn

Đề bài

Cho hai đường tròn \((O\,;\,R)\) và \(({O'}\,;\,{R'})\) cắt nhau tại hai điểm A và B. Trên đường thẳng AB, lấy điểm C ở ngoài hai đường tròn và kẻ hai tiếp tuyến CE, CF đến hai đường tròn đó ( E, F là các tiếp điểm). Chứng minh rằng CE = CF.

Lời giải chi tiết

 

Ta có 

\(\eqalign{
& {\wp _{{C_{/(O)}}}} = \overrightarrow {CA} .\overrightarrow {CB}  = C{E^2} \cr 
& {\wp _{{C_{/({O\,'})}}}} = \overrightarrow {CA} .\overrightarrow {CB}  = C{F^2} \cr 
& \Rightarrow \,\,\,CE = CF \cr} \)

Chú ý:

Hai công thức ở trên là sử dụng công thức trang 50 SGK Hình học 10 nâng cao. Các em cũng có thể chứng minh chi tiết như sau:

Áp dụng công thức phương tích của điểm C với hai đường tròn ta có:


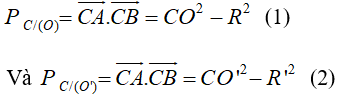
*Do CE là tiếp tuyến của (O) nên tam giác CEO vuông tại E.

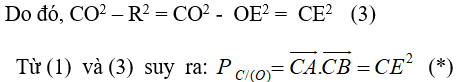
* Do CF là tiếp tuyến của (O’) nên tam giác CFO’ vuông tại F.

Loigiaihay.com


Bình chọn:
3.8 trên 5 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store