Bài 10 Trang 152 SGK Đại số và Giải tích 12 Nâng cao

Không tìm nguyên hàm hãy tính các tích phân sau:

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Lựa chọn câu để xem lời giải nhanh hơn

Không tìm nguyên hàm hãy tính các tích phân sau:

LG a

\(\int\limits_{ - 2}^4 {\left( {{x \over 2} + 3} \right)dx} ;\)

Lời giải chi tiết:

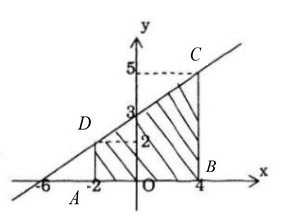
Vẽ đồ thị y=(x/2)+3, các đường thẳng \(x=-2,y=4\).

Tích phân cần tính là diện tích của hình phẳng giới hạn bởi đồ thị y=x/2+3, các đường thẳng x\-2, x=4 và trục hoành.

Tích phân đó bằng diện tích hình thang ABCD với AD=2, BC=5, AB=6.

Diện tích đó là \(\left( {2 + 5} \right){6 \over 2} = 21.\)

Vậy \(\int\limits_{ - 2}^4 {\left( {{x \over 2} + 3} \right)dx = 21} .\)

LG b

\(\int\limits_{ - 1}^2 {\left| x \right|} dx\)

Lời giải chi tiết:

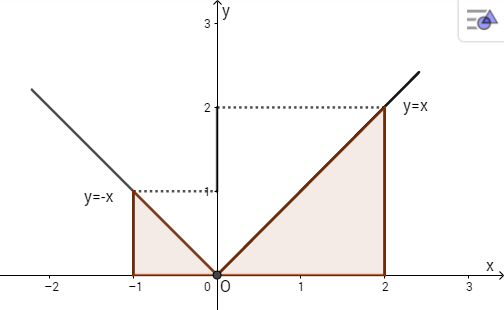
Vẽ đồ thị y=|x|

Diện tích hình phẳng giới hạn bởi y = |x|, trục hoành x = -1, x = 2 bằng tổng diện tích tam giác vuông tô màu.

Từ hình trên ta thấy hình A gồm 2 tam giác.

Do đó tích phân bằng diện tích của A và bằng:

\({1 \over 2}.1.1 + {1 \over 2}2.2 = 0,5 + 2 = 2,5\)

Vậy \(\int\limits_{ - 1}^2 {\left| x \right|} dx = {5 \over 2}\).

LG c

\(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx\)

Phương pháp giải:

Áp dụng định lí 1.

Lời giải chi tiết:

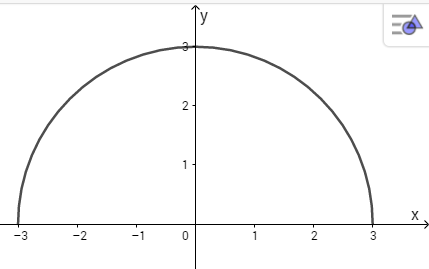
Vẽ nửa đường tròn \(x^2+y^2=9\).

Tích phân bằng diện tích nửa hình tròn \({x^2} + {y^2} = 9\)(hình).

Đây là đường tròn tâm là gốc tọa độ bán kính là R=3.

Do đó diện tích nửa hình tròn là \(\dfrac{1}{2}\pi {R^2} = \dfrac{1}{2}\pi {.3^2} = \dfrac{{9\pi }}{2}\)

Vậy \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx = 4,5\pi \)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài 11 Trang 152 SGK Đại số và Giải tích 12 Nâng cao
hãy tính
Bài 12 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
Hãy tính
Bài 13 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
Chứng minh rằng
Bài 14 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
a) Một vật chuyển động với vận tốc . Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm đến thời điểm . b) Một vật chuyển động chậm dần với vận tốc . Tính quãng đường mà vật di chuyển được từ thời điểm đến thời điểm mà vật dừng lại.
Bài 15 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
Một vật đang chuyển động với vận tốc 10 m/s thì tăng tốc với gia tốc . Tính quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc.
Bài 16 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu 25 m/s. gia tốc trọng trường là .